Wrote

Hi Ioan. As first comment, now I see that you use L as the length of the rigid catenary, meanwhile I use it as length of the elastic one. Also, I'm not sure about the parameter E, if it is in kN, kN/m or kN/m^2. Usually, one identify the parameters by its units, but the differential equation can have some units inconsistencies, derived from the convention that parametric curves have not units. For instance, I don't know if assign the unit meter to the curve parameter p, which is more consistent with the units in the ODE...

Hi Alvaro,

Thanks for your feedback.

I feel useful to add some explanations concerning my developments because I recognize that it is poorly documented.

In my work I try to satisfy two antagonisms: i) That of Engineering – to affect information with units – this is magnificently served by Smath; ii) That of Mathematics, where it is preferable to avoid units, as much as possible.

An example of my practice is here:



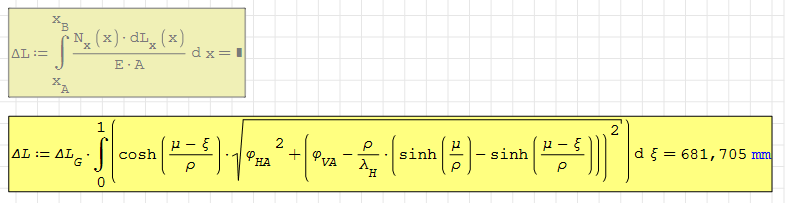
First formula is a classic Strength of Materials one, with units inside. In the second formula, I operated some transformations, targeting to avoid units inside the integral, making it so more robust.

As for input information, I used only 3 (H;V;L) data for inextensible cable and I added 3 (w; A; E) data for the elastic cable; they are: A = area of the cable section (Surface units); w = uniform vertical load along the cable line (Force / Length); E = elasticity (Young) modulus (units Force/Surface).

Best regards,
Ioan