Hello,

I found a bug when accessing not assigned positions within a matrix.
In the following example I assigned on variable 'a' a matrix with two rows and one column.
Now when I access not assigned rows or columns I also get values back.
See my example below:
SMath Version 0.95



Best Regards,
Infinity

Hello Infinity,

I suppose it has something with internal representation of matrix with mat() function:


Hmm...I am not sure if it could be accepted as a feature or a bug
I prefer this to be regarded as a bug.

Regards,
Radovan

Yep, it's a bug. Will fix.

Thank you and regards.

Wrote

Yep, it's a bug. Will fix.

Thank you and regards.

However, ... what would be nice is if, in Matlab style, a single index could point into a 2D matrix

[albumimg]48[/albumimg]

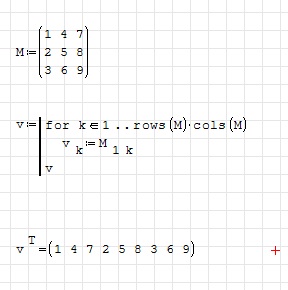
(ie, the first index in this case would not be needed) ... except I'd prefer it if the indexing took place in column order rather than row order.

Stuart

[MATH]M:mat(1,4,7,2,5,8,3,6,9,3,3)[/MATH]

[MATH]v:line(for(k,range(1,rows(M)*cols(M)),el(v,k):el(M,1,k)),v,2,1)[/MATH]

[MATH]transpose(v)=mat(1,4,7,2,5,8,3,6,9,1,9)[/MATH]

... sorry, that first MATH line is supposed to be a 3x3 matrix and the second MATH line is supposed to be showing a program: v:line(for(k,range(1,rows(M)*cols(M)),el(v,k):el(M,1,k)),v,2,1)

[MATH]for(k,range(1,rows(M)*cols(M)),el(v,k):el(M,1,k))[/MATH]

Hello,

It crossed my mind that stack(1) and augment(1) might be made to be used with a single argument - matrix with more than one row and one column - in that way that stack(M) will make a column vector by placing matrix columns one below the other and augment() will make a row vector by placing matrix rows next to each other.

Regards,
Radovan

Hi

an alternative way to transform a matrix in a vector, whitout loops (could be useful for large matrices, I think)



here is the file in the image: mat2vector.zip


regards,

w3b5urf3r

Fixed, with improvement:

Wrote

However, ... what would be nice is if, in Matlab style, a single index could point into a 2D matrix

[albumimg]48[/albumimg]

(ie, the first index in this case would not be needed) ... except I'd prefer it if the indexing took place in column order rather than row order.

Regards.

I guess that indexing order (row or column) is a matter of taste. As I understand Andrey's post, the default order is going to be changed from row order in 0.95 to column order.

This is what 0.95 does:

[MATH lang=eng]M:mat(1,4,7,2,5,8,3,6,9,3,3)[/MATH]

[MATH lang=eng]for(i,range(1,rows(M)*cols(M)),el(v,i):el(M,1,i))[/MATH]

[MATH lang=eng]transpose(v)=mat(1,4,7,2,5,8,3,6,9,1,9)[/MATH]

Accessing the transpose should provide column ordering:

[MATH lang=eng]for(i,range(1,rows(M)*cols(M)),el(v,i):el(transpose(M),1,i))[/MATH]

However, the result is a complaint, that the requested element does not exist.

If the matrix is transposed in advance, the trick works:

[MATH lang=eng]M:transpose(M)[/MATH]

[MATH lang=eng]for(i,range(1,rows(M)*cols(M)),el(v,i):el(M,1,i))[/MATH]

[MATH lang=eng]transpose(v)=mat(1,2,3,4,5,6,7,8,9,1,9)[/MATH]

Also, use of eval works.

[MATH lang=eng]for(i,range(1,rows(M)*cols(M)),el(v,i):el(eval(transpose(M)),1,i))[/MATH]

I don't have an idea, how to explain these differences.

Slightly off topic: IMHO linear indexing in general does not contribute to the readability of algorithms (the reader must make assumptions on row or column ordering). In contrast to this I would highly welcome another matlab feature: impicit iteration over vector valued indices.

They would be a highly welcome equivalent to Mathcad range variables and are consistent to the usual math notation.

Best regards, Martin Kraska

Wrote

I guess that indexing order (row or column) is a matter of taste.

Yes.

Quote

As I understand Andrey's post, the default order is going to be changed from row order in 0.95 to column order.

That is my understanding too.

Quote

...IMHO linear indexing in general does not contribute to the readability of algorithms (the reader must make assumptions on row or column ordering).

Although the reader may not be able to implicitly determine the element order for a single index into an array, this is, I believe, one of those cases where the application's rules determine the interpretation, as in Matlab. The ability to use a single index is potentially useful for multi-dimensional array (MDA) indexing (where the number of dimensions can be arbitrarily large).

Quote

In contrast to this I would highly welcome another matlab feature: impicit iteration over vector valued indices.

They would be a highly welcome equivalent to Mathcad range variables and are consistent to the usual math notation.

The whole topic of array handling is probably worthy of separate discussion, covering, for example, indexing of multi-dimensional arrays, nested arrays and tensors.

... if such things as MDAs and tensors are for the distant future, then I propose that the provision of IsArray, IsScalar and IsFunction functions would be immediately useful for manipulating nested arrays and a more direct indexing for nested arrays would be beneficial, eg nested indexing on left hand side of an assignment or el having as many arguments as are necessary to index an arbitrarily deep nested array.

[albumimg]49[/albumimg]

Stuart

Wrote

Fixed, with improvement:.

I just played with the update and I see that a single-index returns the results in row order.

A note from one of the Wiki tutorials:
"It is important to indicate that even though you can form row vectors, many of the matrix and vector functions defined in SMath Studio apply only to column vectors. Thus, column vectors are considered true vectors for the purpose of matrix operations in SMath"

If one creates a vector by use of a single indexing then the result is a column vector. So, for a 3x3 array my expectation would be that, dropping the second (column) index would be equivalent to retaining the first (row) index and that M₂ would return M_2,1 rather than M_1,2. There is a lot of Matlab and Mathcad code out there that could be mapped to SMath and it would seem to make sense to use an indexing order that requires less modification to get it to run under SMath.

Just a thought, before the feature gets into regular use ...

Stuart

Hello,

here are my observations with build 4559. Highlighting is done for what I think is inconsistent.

• linear indexing using just index values beyond the limits is now suppressed ("Requested matrix element does not exist" ):
  
  [MATH lang=eng]el(mat(1,2,3,4,5,6,7,8,9,3,3),1,5)=#@#[/MATH]
  
  
• linear indexing using a single index works as announced, uses row ordering:
  
  [MATH lang=eng]el(mat(1,2,3,4,5,6,7,8,9,3,3),4)=4@#[/MATH]
  
  
• linear indexing beyond the number of elements is now suppressed. The error message "Argument doesn't match to expected kind" is wrong. Should be "Requested matrix element does not exist"
  
  [MATH lang=eng]el(mat(1,2,3,4,5,6,7,8,9,3,3),10)=#@#[/MATH]
  
  
• linear indexing does not work with matrix-valued functions (like transpose, inverse, etc), unless they are "eval"uated. Message "Argument doesn't match to expected kind"
  
  [MATH lang=eng]el(transpose(mat(1,2,3,4,5,6,7,8,9,3,3)),7)=#@#[/MATH]
  
  
• column ordering is achieved by the following slightly cumbersome expression
  
  [MATH lang=eng]el(eval(transpose(mat(1,2,3,4,5,6,7,8,9,3,3))),7)=3@#[/MATH]
  
  
• Nested el work (but do not try to transpose any of the sub-matrices)
  
  [MATH lang=eng]el(el(el(mat(1,2,3,4,mat(1,2,3,4,5,6,7,8,mat(1,2,3,4,5,6,7,8,9,3,3),3,3),6,7,8,9,3,3),5),3,3),7)=7@#[/MATH]
  
  

I would expect el(1), i.e. linear indexing, to work on any matrix valued function. Currently, it seems to work for expressions of type mat() and el(). el(2) has no problems with matrix valued functions:

[MATH lang=eng]el(el(el(mat(1,2,3,4,mat(1,2,3,4,5,6,7,8,transpose(mat(1,2,3,4,5,6,7,8,9,3,3)),3,3),6,7,8,9,3,3),5),3,3),1,2)=4@#[/MATH]

Best regards, Martin