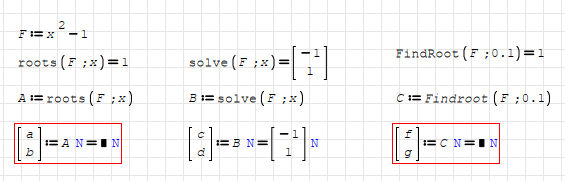Multiply of a numeric vector times a unit fails. - Messages
Multiplying this vector times a unit fails.
Mitigation is possible when using vectorize() or the custom simp() function. Yet it is strange why these tricks should be used. Multiplying a numerical vector times a scalar unit usually is no problem. Any idea?
1-2-Maßeinheiten.sm (116.57 KiB) downloaded 1016 time(s).
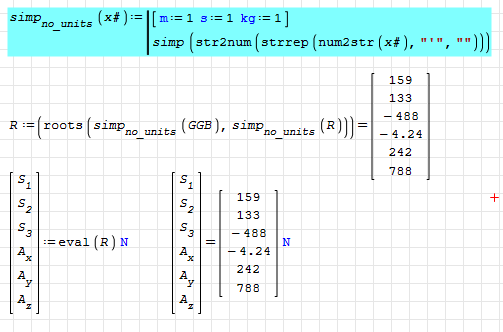
Just like vectorize() this is another workaround. What is special with my vector R? It is stored as a column vector of numbers. Multiplying this with a unit should not require poking around for workarounds. I consider the behaviour being a bug.
Possibly, the preview (and also the storage display in the debugger) are unreliable and there is some hidden issue in the stored value of the variable R. That, however, would be a much bigger problem, because referring to the stored value for understanding what happens, would be at least partially pointless.

Wrote... Just like vectorize() this is another workaround. What is special with my vector R? It is stored as a column vector of numbers. Multiplying this with a unit should not require poking around for workarounds. I consider the behaviour being a bug.
Yes, you're right: using eval is just another workaround, like the others that you present. I thought this might be a solution to the problem, but it really isn't. Perhaps I thought this because of the habit of resorting to evalb (eval as boolean) and evalm (eval as matrix) in older versions of Maple.
Wrote... Possibly, the preview (and also the storage display in the debugger) are unreliable and there is some hidden issue in the stored value of the variable R. That, however, would be a much bigger problem, because referring to the stored value for understanding what happens, would be at least partially pointless.
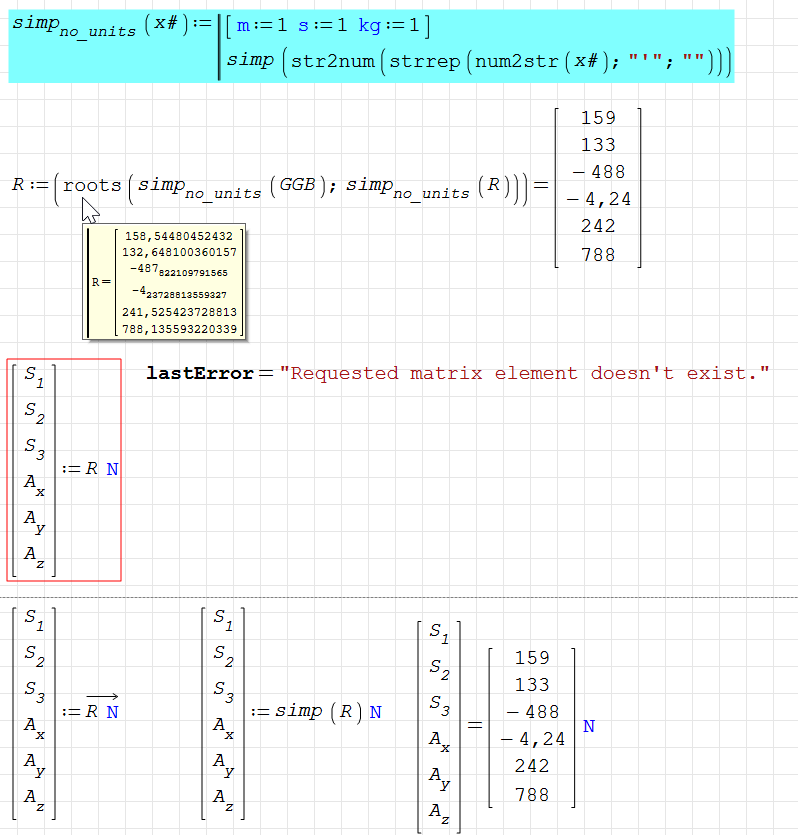
If there's a bug, it might be in the multiple assignment. Using an intermediate variable, you can see why the dimensions don't match. However, since SMath doesn't run the calculations unless explicitly requested with eval, it's not clear why it works with eval(R)*'N, when by that theory it should be eval(R*'N). In the following image, all the optimizations are numerical.

Best regards.
Alvaro.
Wrote
If there's a bug, it might be in the multiple assignment. Using an intermediate variable, you can see why the dimensions don't match. However, since SMath doesn't run the calculations unless explicitly requested with eval, it's not clear why it works with eval(R)*'N, when by that theory it should be eval(R*'N). In the following image, all the optimizations are numerical.
Best regards.
Alvaro.
I think that the multiple assignment can't be blamed per se, because in my previous post the multiple assignment works without eval() or other tricks (demonstrated with the vector v). So my question still is the same: What makes my vector so special that the behaviour is different?
I think this is important for a predictable user experience.
WroteCan roots() be the problem?
Actually, only solve() can do it right.
I don't think that roots() or FindRoots() are to blame here. Other than solve() they don't scan a range for multiple solutions. Based on an initial guess they just return a single solution just like the Newton-Raphson algorithm. The dimension of the solution of roots() and FindRoots() matches the dimension of the vector of variables. Given a single scalar equation and a single variable there is no vector result to be expected, thus assigning the result to a vector of variables must fail.
Assignment of the solve() result succeeds because the equation happens to have two solutions in the search region (implicitly given by the UI setting).
- New Posts
- No New Posts