Dear to all,
I found some topics in the forum, but I'm a little bit confused.
Someone could help me?
Thank
D

Hi. You can try maple or Maxima plugin. Or dot numerics plugin and your own code and check when each one it's better, like in the attached.

MEigen.sm (78 KiB) downloaded 91 time(s).
MEigen.pdf (154 KiB) downloaded 72 time(s).

Best regards.

Dear Razonar and Giraud,
thank you very much!!!
D

Dear all,
I tried both version proposed, but with my matrix they don't work.
Where is the mistake?

Natural frequencies.sm (219 KiB) downloaded 53 time(s).

On the other hand I tried to use MAPLE, but I don't understand how to use it....

Thanks
D

Wrote

Dear all,
I tried both version proposed, but with my matrix they don't work.
Where is the mistake?

Hi. You found with dot numerics eigenvalues and vectors, or at least something probably useful answer. About the code in MEigen, don't expect too much, with that few code lines.

From the book Numerical Recipes in C:



and



About the use of maple it returns eigenvalues into an structure, which could be complicated to get in SMath: Maple help

Finally, even the eigenvectors are very powerful theoretically given that you can get the Jordan Canonical Form with them and thus study any lineal system with it, from the numerical point of view it's better study the same system using singular value decomposition, which it's more stable and have procedures for know the error and stability of the answers.

Best regards.
Alvaro.

Dear Jean,
I apologize, but I'm not so expert and I don't understand too much.

1) I tried with the suggestion from Razonar: eigenvalue is ok, eigenvector seem yes, but the part below aren't solved and I the message is "Result is above max allowed positive number"



2) Also, with your file: eigenvalue is ok, eigenvector seem yes, but the calculation is "locked" and don't proceed over the point below:



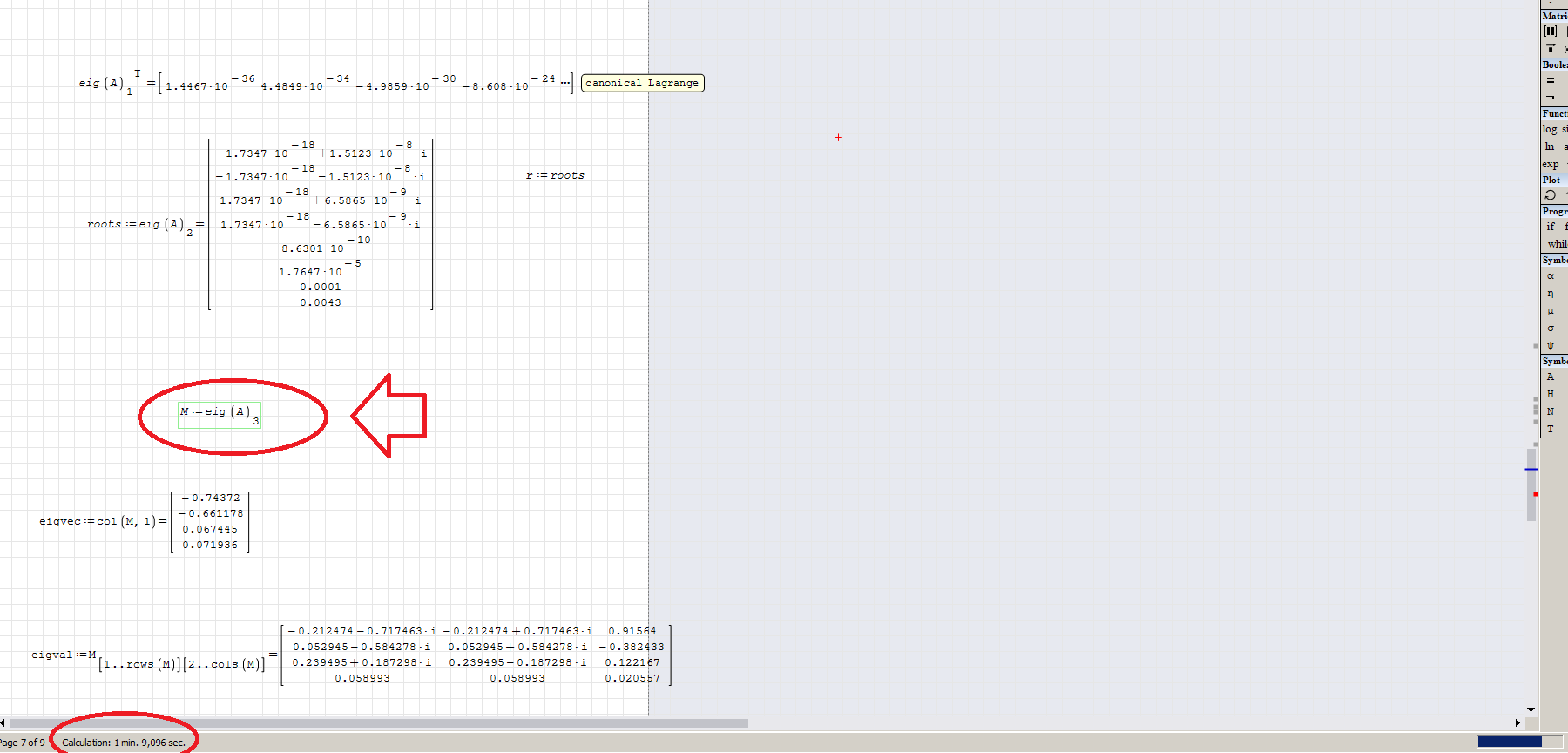
and if wait the time running...

Thanks
Davide

Wrote

1) I tried with the suggestion from Razonar: eigenvalue is ok, eigenvector seem yes, but the part below aren't solved and I the message is "Result is above max allowed positive number"

Hi. This version try to avoid the numerical issue. Notice that the eigenvalues (obtained with the SMath polyroots function, which can't be the better method) are different from those from dot numerics.

Although surprisingly I get a decomposition that does not differ from the expected one, that is norme (A * MM * diag (λ)) = 0, I would not rely too much on the twelve lines of code of my function to calculate something as unstable as eigenvalues and eigenvectors and I would put more hope in the dot numerics results.

Natural frequencies.sm (243 KiB) downloaded 80 time(s).
Natural frequencies.pdf (876 KiB) downloaded 83 time(s).

Best regards.
Alvaro.

Dear Jean and Razonar,
as first I apologize for my late answer.
Thank for the support
Bye
Davide