allow division by zero - Messages
I suggest enabling division by zero, resulting in infinity (I hope this will not break things?).
WroteDividing a number by infinity gives zero.
I suggest enabling division by zero, resulting in infinity (I hope this will not break things?).
I understand what you are saying. Division by 0 always results from
driving the horse crazy. Discretise to escape 0 thar will do.
Smath is missing "NaN" [Not a Number] ^307
Even if you have 1/0=inifinity, that won't solve the problem, neither plot.
Cheers Mike, Jean
My point is to remove one of possible error conditions when programming is difficult in SMath. In another post, you say that you couldn't mimick OnError function. My proposal lies in the same plane: I would like to be able to write more robust programs.
Lat's say I write a solver (inside SMath, not a plugin). I pass to it a function, and some range(s). While solving, it may encounter some extremum, where the function performs division by zero. In this case, SMath simply stops the block, emitting the error.
You may say that "you should plot before solving", or somesuch. But you live in some imaginary world. Real stuff must be designed fool-proof if it is to be used by other people. So, my proposal could eliminate one possible problem here, allowing program to continue in these cases.
.WroteNaN isn't appropriate here. You may look at floating-point specs to see when NaNs are generated.
My point is to remove one of possible error conditions when programming is difficult in SMath. In another post, you say that you couldn't mimick OnError function. My proposal lies in the same plane: I would like to be able to write more robust programs.
Lat's say I write a solver (inside SMath, not a plugin). I pass to it a function, and some range(s). While solving, it may encounter some extremum, where the function performs division by zero. In this case, SMath simply stops the block, emitting the error.
You may say that "you should plot before solving", or somesuch. But you live in some imaginary world. Real stuff must be designed fool-proof if it is to be used by other people. So, my proposal could eliminate one possible problem here, allowing program to continue in these cases.
You have good points Mike. But even the advanced Mathcad "root" needs be initialised, that's where the plot will guide. It is a very robust solver but occsionally fails. It is like all common solvers [including Smath], it is a non seeded solver ... in other words: it does not track itself in flat or abrupt regions where non seeded solvers fail.
If you pass a range, inevitably it will encounter the divide by 0 if the function has such a feature. Then don't pass a range, pass a discrete vector that you have checked it escapes the divide by zero.
That's not all and far to be solvable in Smath. The silent worm in any and all computing machinery is the granularity of the binary system. When two results fall within the granularity of the function and the machine, the sytem goes paralysed. Mathematica 4.0 will issue a blue page [sometimes more than one page] full of "not a machine number", it still finishes the project but with so many values not computed. If you wanted a vector of solutions 100 long and get the two firt values and few more anywhere along: Oh ! the job is not done.
No one has yet found the "binary worm insecticide" !
Mathcad "root" is an improved version of "Numerical recipes".
Eventually, the "Quantum computer" will help reducing granularity.
Jean
Not same with Smath: you still have 25.06625827963098
Enough to share a Vodka with me ?
Read carefully the last image from Mathcad: can you see what is granularity ?
Mathcad starts being granular @ much-much lower values than Smath.
Mathcad 11 was a true 64 extended floating point. Smath 5346 is 32 bits.
It does not have true floating point representation, max 15 decimals.
OK you may get symbolic fraction.
Jean

Untitled Granularity.sm (43.6 KiB) downloaded 1037 time(s).
SMath isn't 32-bit. It is .NET program, and uses OS bitness. On my 64-bit machine, it is 64-bit.
It only SHOWS 15 digits, but uses full available floating-pont representation.
It's funny how you provide Mathcad example images, but don't put SMath exact counterparts side-by-side.
On my machine, it gets exactly same results as you say Mathcad does.
Or maybe I get you wrong?
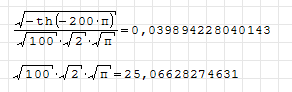

Granularity, heh. It's perfectly known, and something you should account for when doing computer-aided floating-point math. Many people devote great effort to develop good strategies for this. See for example here: https://randomascii.wordpress.com/category/floating-point/
But that's not the point of my proposal!
Why do you keep changing the topic each time? It may only distract those who it is addressed to!
In this example, just instruct Smath to skip divide by zero.
Easy in mathcad => "on error". If you can code the "on error"
I might be able to complete the image rotation by angle.
Smath 5346 XP is 32 bits. If it would be 64 bits I would get
same result [or about same] than Mathcad 11. Just calculate
the example in the Granularity.sm @ the same values than Mathcad.
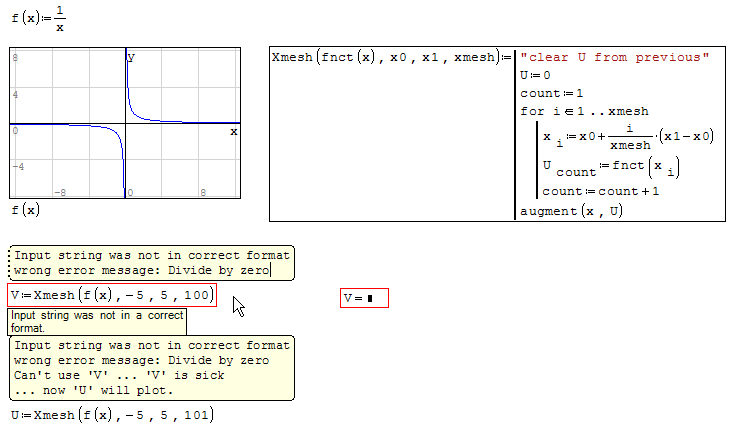
Smath quick plot manages to plot 1/x. For discrete tasks: NOT
unless you manage to escape the zero.
Jean
That's the very idea I talk about. But here, the infinity is ccorrect answer. You may test if it's infinity, if you please.
That SMath is 32-bit at your computer, it's normal. It's not Mathcad, so don't try to convince everybody that it must always behave just like Mathcad. Only if its results are wrong (taking into account its current bitness), and only if you use current version, it's correct to argue that SMath should improve here. Using outdated version isn't good, because you declare problems that could well be fixed already.
The "wrong error message" is actually somewhat correct. SMath takes passed function, tries to execute it with an argument, and gets error. It doesn't propagate the exact error from the function to you, (which is a pity), but instead informs you, that an argument (input to function) wasn't correct.
Though I would prefer it to say something like this:
"fnct(0): the input is incorrect: Division by zero".
they come fom Windows, Padé rational fraction @ 21 digit floating points that Windows
conventionalised to display 15 decimals. For higher accuracy and greater stability,
"Big blues" run Chebyshev 25 'true' or near true decimals. For more decimals like in
Mathcad, they run "continued fraction".
Cheers, Jean
WroteNO PC user software calculate sin, cos ...
they come fom Windows, Padé rational fraction @ 21 digit floating points that Windows
conventionalised to display 15 decimals. For higher accuracy and greater stability,
"Big blues" run Chebyshev 25 'true' or near true decimals. For more decimals like in
Mathcad, they run "continued fraction".
Another bold claim. You tell this to the person (which blog I directed you to) who spent quite some time doing maths for Valve (one of most prominent PC gaming company), ans now does that for Google... oh my! you surely know better what PC user software does.
By the way, PC != Windows. And WinAPI doesn't include sin, cos, ... - their "standard" implementations come from their corresponding programming languages standard libraries. Those libraries are created by programmers, vary between compilers, are improved over time. They may use hardware to get results, or some algorithms, or both. And there exist great many non-standard libraries (also created by people), that aim to provide a better precision, or better performance, or use better algorithms that don't make errors like those used by standard libraries, or deal with fractions instead of floats, or whatever.
I don't understand "PC gaming company" ?
Do you mean company designing 'kids games' ?
Not so long ago for games on ordinary PC Windows
they disabled the floating point. How many Mathsoft
Collabs had this problem after their kids 100's + 100's.
Easy to repair: run "RegTool", to register back the FPU.
Cheers, Jean => bed time.
Untitled Granularity.sm (56.2 KiB) downloaded 1039 time(s).
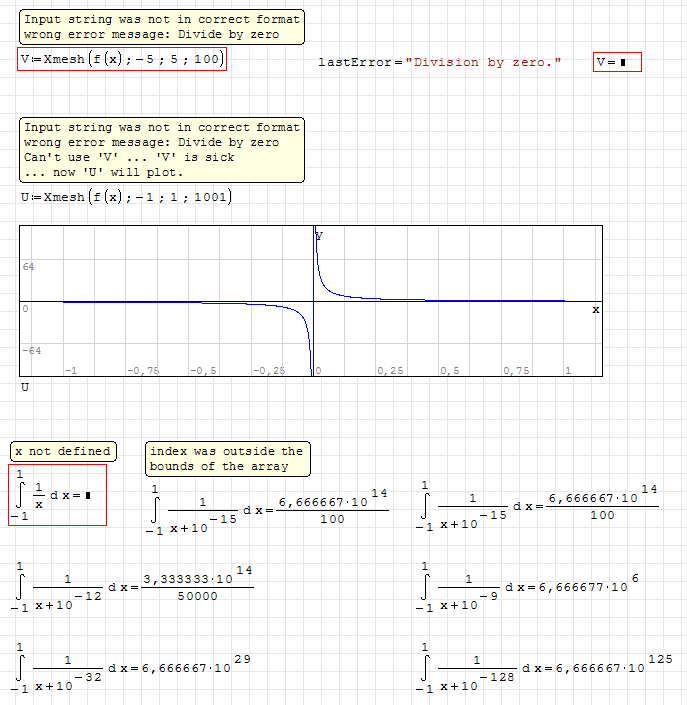
The error message is "fixed" - if I understand your concern properly. If only it could do what I ask for - there wouldn't be that error in the first place.
The first integral isn't calculated. But that's outside of this proposal's scope.
Others calculate properly.
sqrt(-th(-73*π)) gives 1, as well as sqrt(th(114*π)).
q(0.01) gives 0.039894.
Maybe it's time to update?
WroteMaybe it's time to update?
NO: it's not time to update. As far as for my Engineering works
and clients, Smath 5346 is stable enough compared to the latest
beta(s) with so many reported problems in this forum. I downloaded
5346 July 2015, if you tell me it's so obsolete and abandonned,
when the latest version will be "Museum" ? the day Smath will
"allow divide by zero" ! I showed how to escape "divide by zero",
so that it "allows divide by zero".
Cheers Mike, Jean
Wrotejust instruct Smath to skip divide by zero.
Easy in mathcad => "on error". If you can code the "on error"
I might be able to complete the image rotation by angle.
Here it is!
- New Posts
- No New Posts