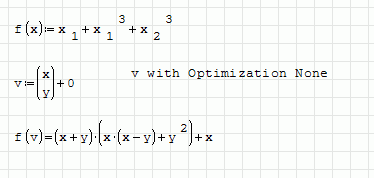1 Pages (9 items)
Hessian - Messages
#2 Posted: 10/2/2012 2:27:02 AM
:d
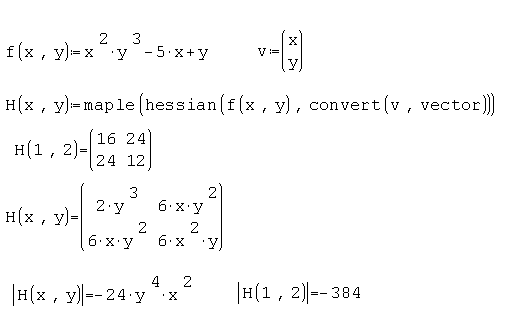
Russia ☭ forever, Viacheslav N. Mezentsev
1 users liked this post
Radovan Omorjan 10/2/2012 3:04:00 AM
#4 Posted: 10/2/2012 3:36:06 AM
#6 Posted: 10/6/2012 3:17:29 AM
I think that this is the better way to work with the Jacobian.
Alvaro.
Jacobian.sm (22.57 KiB) downloaded 907 time(s).
Alvaro.
Jacobian.sm (22.57 KiB) downloaded 907 time(s).
#7 Posted: 10/6/2012 7:24:02 AM
Hello Alvaro,
But what to do if the vector function is defined this way?
[MATH=eng]Φ(X,t):-5*t*mat(el(X,1),el(X,2),2,1)+mat(el(X,2)*el(X,1)^2,el(X,2)^2*el(X,1)^2,2,1)[/MATH]
It will not work until t is a constant (scalar). Take a look at the pictures please.
Regards,
Radovan

But what to do if the vector function is defined this way?
[MATH=eng]Φ(X,t):-5*t*mat(el(X,1),el(X,2),2,1)+mat(el(X,2)*el(X,1)^2,el(X,2)^2*el(X,1)^2,2,1)[/MATH]
It will not work until t is a constant (scalar). Take a look at the pictures please.
Regards,
Radovan

When Sisyphus climbed to the top of a hill, they said: "Wrong boulder!"
#8 Posted: 10/6/2012 3:26:35 PM
#9 Posted: 10/7/2012 2:40:21 AM
Hello Alvaro,
Actually, that is the point. I think that's the problem of the symbolic engine.
The first one gives the symbolic result
[MATH=eng](-5*t)*mat(el(X,1),el(X,2),2,1)+mat(el(X,2)*el(X,1)^2,el(X,2)^2*el(X,1),2,1)=mat(-5*el(X,1),-5*el(X,2),2,1)*t+mat(el(X,2)*el(X,1)^2,el(X,2)^2*el(X,1),2,1)[/MATH]
and the result is not a vector, therefore length() does not work.
The second one actually give you the vector symbolically
[MATH=eng](-5)*mat(el(X,1)*t,el(X,2)*t,2,1)+mat(el(X,2)*el(X,1)^2,el(X,2)^2*el(X,1),2,1)=mat(el(X,1)*(-5*t+el(X,2)*el(X,1)),el(X,2)*(-5*t+el(X,2)*el(X,1)),2,1)[/MATH]
Maybe the solution would be to say in advance what the variable t was - either scalar, vector or matrix. Something like "assume". If SMath assumed that t was a scalar, it should behave in accordance to that and give you the second correct result.
Regards,
Radovan
Actually, that is the point. I think that's the problem of the symbolic engine.
The first one gives the symbolic result
[MATH=eng](-5*t)*mat(el(X,1),el(X,2),2,1)+mat(el(X,2)*el(X,1)^2,el(X,2)^2*el(X,1),2,1)=mat(-5*el(X,1),-5*el(X,2),2,1)*t+mat(el(X,2)*el(X,1)^2,el(X,2)^2*el(X,1),2,1)[/MATH]
and the result is not a vector, therefore length() does not work.
The second one actually give you the vector symbolically
[MATH=eng](-5)*mat(el(X,1)*t,el(X,2)*t,2,1)+mat(el(X,2)*el(X,1)^2,el(X,2)^2*el(X,1),2,1)=mat(el(X,1)*(-5*t+el(X,2)*el(X,1)),el(X,2)*(-5*t+el(X,2)*el(X,1)),2,1)[/MATH]
Maybe the solution would be to say in advance what the variable t was - either scalar, vector or matrix. Something like "assume". If SMath assumed that t was a scalar, it should behave in accordance to that and give you the second correct result.
Regards,
Radovan
When Sisyphus climbed to the top of a hill, they said: "Wrong boulder!"
1 Pages (9 items)
- New Posts
- No New Posts