Hi All -

I've recently discovered Smath, and have dove in headfirst.

Because of my work, I can't share much of what I do but I'd like to give back to the community as well as take - even if it's only a little bit.

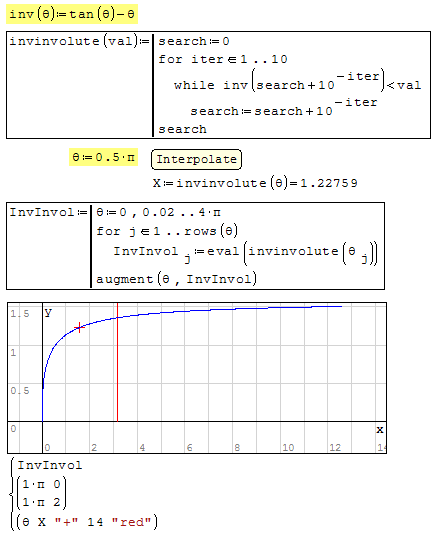
With that said - in my daily life I do a lot of work with gears. When doing calculations, the involute function - and more importantly its inverse - always come up.

The best and most accurate method we have found for solving the inverse is an iterative method.

Attached is the snippet I've been using at the top of many of my worksheets.

Hope it helps someone else!

Dan
InvoluteCalcs.sm (3 KiB) downloaded 193 time(s).

Like this ? You can only plot discrete. You can inerpolate.

Very nice, Jean

... the "RootOf" reverts to solving with "roots".
We can't get a single plot by bracketing the search,
there is granularity in the solver. I believe the
roots solve is more accurate [sol(x), Sol(x)], just
from educated guess.

Jean

Hello Dan,

I use the function

arcinv(invx):=solve(inv(x)=invx;x;0;π/2)

Peter

All -

Thanks for the quick and informative replies. I have a lot to learn about the software yet.

While the iterative method is accurate enough for what we're doing, I'll probably use the solve() function going forward now that I know how it works. Turns out I had a bit to learn about the different types of = in the software.


Dan

Wrote

Hello Dan,

I use the function

arcinv(invx):=solve(inv(x)=invx;x;0;π/2)

Peter

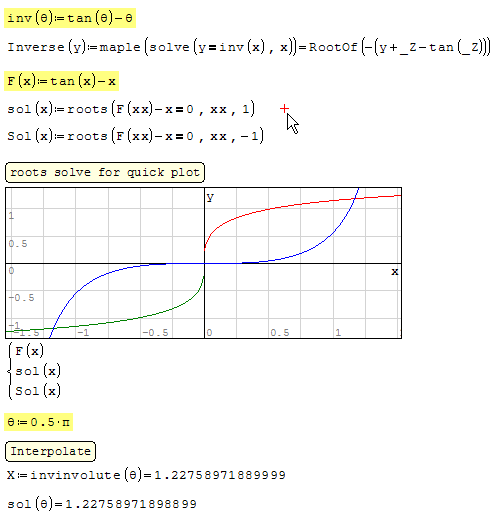
Most interesting, for the longer range. Often, 'solve' is guilty
of inaccuracy. Two examples in the attached proof. Thanks for
visiting and your input. A puzzling application, hard to verdict.

Jean

Solve Involute.sm (28 KiB) downloaded 110 time(s).