1 Pages (13 items)
Maxima crahes SMath with package "interpol" - Turning optimization None crashes Smath - Messages
#1 Posted: 12/1/2013 6:06:27 AM
Here is the problem I bumped into. I was just playing with Maxima package interpol and find out that it crashes SMath for cspline() and linearinterpol() functions when the Optimization is turned to None. I suppose that the charfun2() causes this problem, but do not know why. Please look at the example and try to turn the optimization to None for the red area. If the Symbolic optimization is on, then the error is issued. If I turned Optimization to None, then SMath crashes on my computer.
Regards,
Radovan
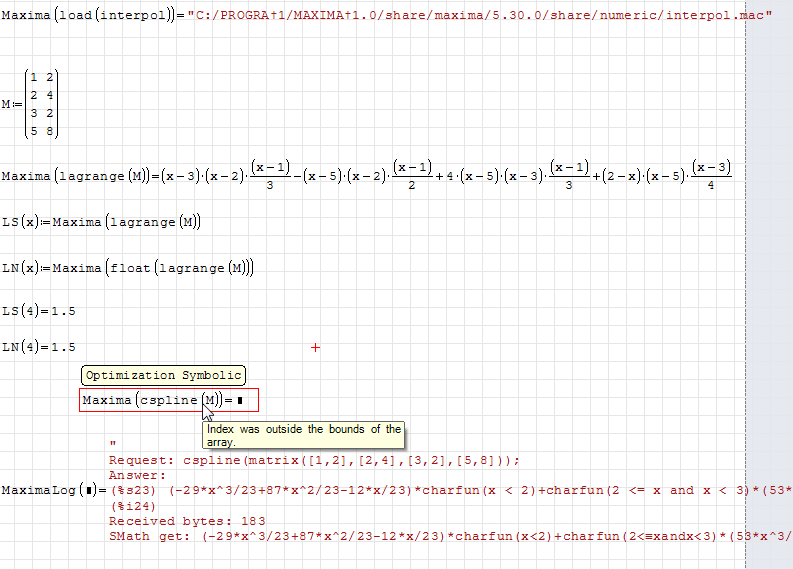
Regards,
Radovan

When Sisyphus climbed to the top of a hill, they said: "Wrong boulder!"
1 users liked this post
Martin Kraska 12/1/2013 6:58:00 AM
#2 Posted: 12/1/2013 7:16:21 AM
On my computer (x64, win 7) setting opt to none in your example just crashes SMath, which is bad enough.
The current plugin version is rather unstable. There are multiple ways to trouble the plugin such that you cannot even recover by MaximaControl("restart" ).
I think we should maintain a stable and a development version in the online gallery.
The current plugin version is rather unstable. There are multiple ways to trouble the plugin such that you cannot even recover by MaximaControl("restart" ).
I think we should maintain a stable and a development version in the online gallery.
Martin KraskaPre-configured portable distribution of SMath Studio: https://en.smath.info/wiki/SMath%20with%20Plugins.ashx
#3 Posted: 12/1/2013 7:42:05 AM
Hello Martin,
I am not sure if this particular problem (bug) might be somehow related to the relational operators in Smath and in Maxima (<= etc.). I remembered you mentioned this somewhere, but can not find it where it was at the moment.
Regards,
Radovan
I am not sure if this particular problem (bug) might be somehow related to the relational operators in Smath and in Maxima (<= etc.). I remembered you mentioned this somewhere, but can not find it where it was at the moment.
Regards,
Radovan
When Sisyphus climbed to the top of a hill, they said: "Wrong boulder!"
#4 Posted: 12/1/2013 7:54:24 AM
Radovan, you are right, part of the problem is that back-translation of relational operators like >= and <= as well as boolean operators like or and and is not yet supported in the plugin. But I shall have a look at charfun, may be that provides a good way to translate Davide's ternary comparison operators to Maxima and back to SMath.
However, the plugin should not crash on unsupported expressions.
However, the plugin should not crash on unsupported expressions.
Martin KraskaPre-configured portable distribution of SMath Studio: https://en.smath.info/wiki/SMath%20with%20Plugins.ashx
1 users liked this post
Radovan Omorjan 12/1/2013 9:14:00 AM
#5 Posted: 12/1/2013 5:06:20 PM
Preview of partly problem solution. Back-translation of logical expressions is implemented and a the interpol results can be evaluated, plotted and numerically integrated. The plugin, however, does not yet wrap boolean expressions in charfun() when translating to Maxima, therefore such expressions cannot yet be integrated using Maxima's int() version.
It seems that expressions involving charfun() cannot be integrated symbolically using Maxima. Thus there might be a point of transforming boolean expressions to such with sign().
We upload the new plugin version as soon as it passes the regression test. Current state is too unstable.
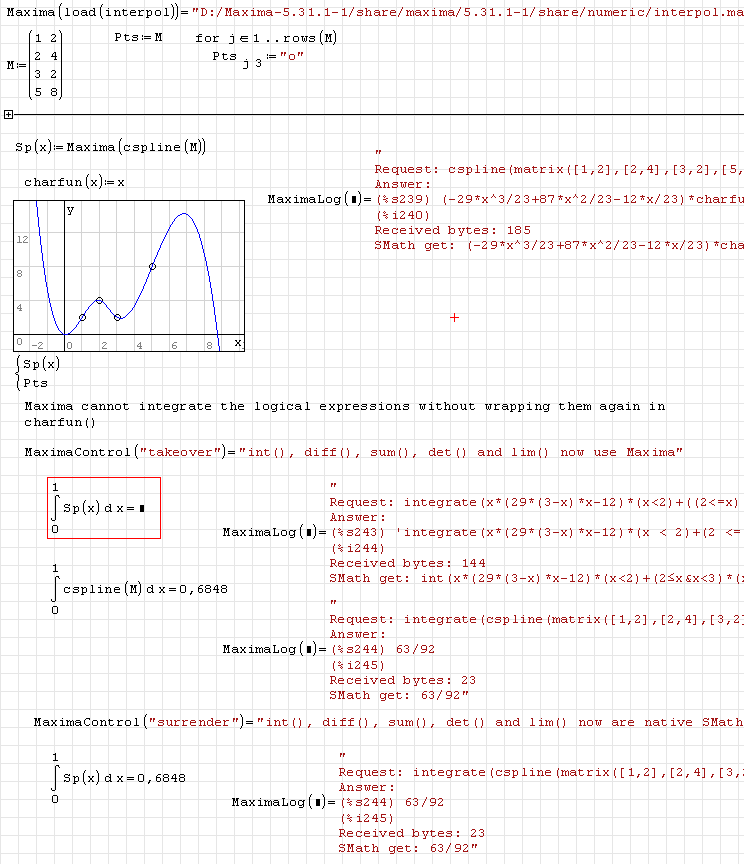
It seems that expressions involving charfun() cannot be integrated symbolically using Maxima. Thus there might be a point of transforming boolean expressions to such with sign().
We upload the new plugin version as soon as it passes the regression test. Current state is too unstable.
Martin KraskaPre-configured portable distribution of SMath Studio: https://en.smath.info/wiki/SMath%20with%20Plugins.ashx
1 users liked this post
Radovan Omorjan 12/2/2013 5:43:00 AM
#6 Posted: 12/2/2013 6:30:30 AM
Thank you Martin,
Actually, I was trying to make a function by using cubic spline from interpol package, and to see how to integrate and differentiate the obtained function numerically - everything by using Maxima. I was already mentioned this few times on the Forum. For instance (see this example Differentiation of splines). Unfortunately, this example will not work for me anymore, do not know why.
Regards,
Radovan
EDIT: Try to plot with both SMath genuine plot and X-Y plot. There are the differences I can not explain
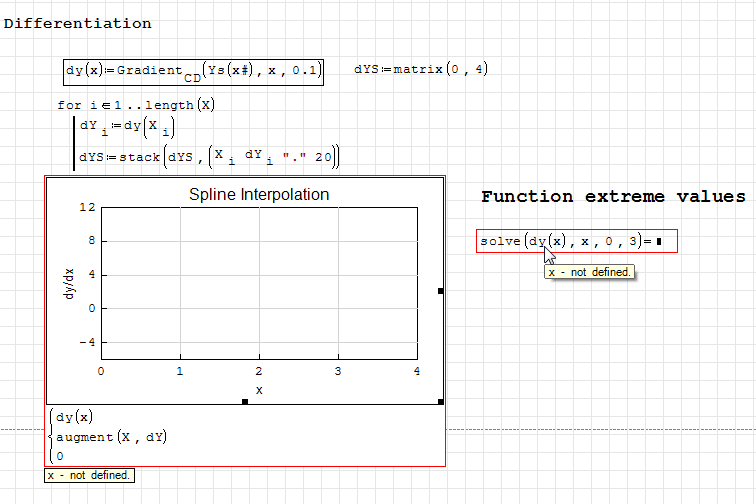
Actually, I was trying to make a function by using cubic spline from interpol package, and to see how to integrate and differentiate the obtained function numerically - everything by using Maxima. I was already mentioned this few times on the Forum. For instance (see this example Differentiation of splines). Unfortunately, this example will not work for me anymore, do not know why.
Regards,
Radovan
EDIT: Try to plot with both SMath genuine plot and X-Y plot. There are the differences I can not explain

When Sisyphus climbed to the top of a hill, they said: "Wrong boulder!"
#7 Posted: 12/2/2013 10:24:12 AM
If you are just up to numeric integration and differentiation of interpolated data, you could sample the interpolation and apply appropriate FIR kernels using uni's alglib functions. Works very well with Savitzky-Golay in matlab.
al_convr1d.sm (21.17 KiB) downloaded 713 time(s).
al_convr1d.sm (21.17 KiB) downloaded 713 time(s).
Martin KraskaPre-configured portable distribution of SMath Studio: https://en.smath.info/wiki/SMath%20with%20Plugins.ashx
#8 Posted: 12/2/2013 12:53:45 PM
Thank you Martin for this one. The sampling was Ok and worked even with Gradiend.CD() from Davide's plugin and that was not the point. The problem was the plotting and solve() which failed here now. Do not know why. Actually, I have no idea at the moment how to find the zeros of dy(x) function from the example Differentiation of splines (see the picture from the example which worked before - but now failed).
Actually, it is a bit out of the topic regarding the Maxima interpol package - but I can not understand why the plotting does not work anymore and do not understand why solve() failed here. It seems to me that I have the same questions over and over. Sorry If I do not see some obvious things - again.
Regards,
Radovan
The attached sm file will not produce this result for the plot and solve() anymore, as seen in the picture
interpdiff-1.sm (12.15 KiB) downloaded 745 time(s).
Actually, it is a bit out of the topic regarding the Maxima interpol package - but I can not understand why the plotting does not work anymore and do not understand why solve() failed here. It seems to me that I have the same questions over and over. Sorry If I do not see some obvious things - again.
Regards,
Radovan
The attached sm file will not produce this result for the plot and solve() anymore, as seen in the picture
interpdiff-1.sm (12.15 KiB) downloaded 745 time(s).
When Sisyphus climbed to the top of a hill, they said: "Wrong boulder!"
#9 Posted: 1/10/2014 8:41:54 PM
#10 Posted: 1/11/2014 5:14:28 AM
Thank you Martin,
Unfortunately, numerical integration in Maxima (quad* set of functions) will not work directly in SMath with this cubic spline. Actually, It must be used this way
[MATH=eng]Maxima(quad_qags(cspline(M),x,1,3))=sys(6.369565217391301,7.071637942785607*10^{-14},63,0,4,1)[/MATH]
Moreover, when I use Davide's, Gradiend.CD() I can get a function by numerically differentiating - but not its roots. This is a long time story, and I still can not figure out how to deal with this kind of problems in SMath.
Regards,
Radovan
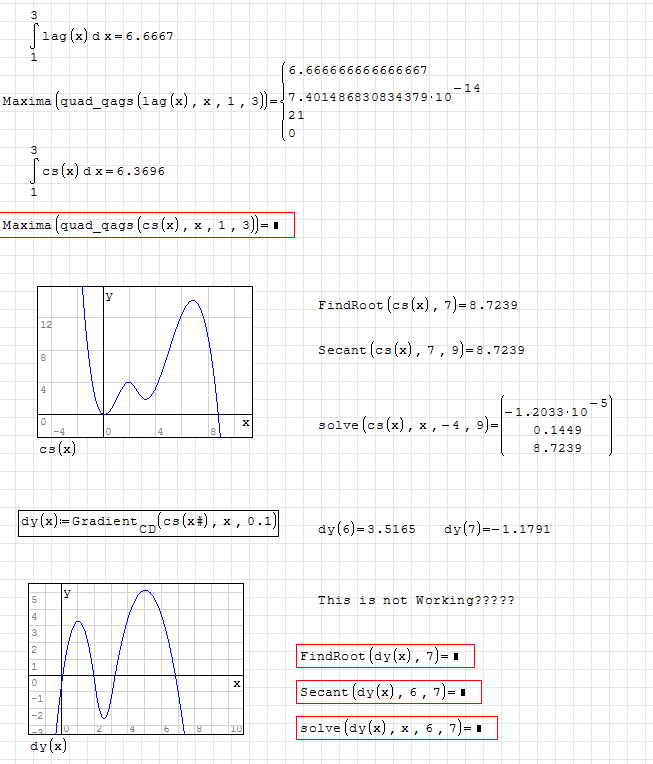
Unfortunately, numerical integration in Maxima (quad* set of functions) will not work directly in SMath with this cubic spline. Actually, It must be used this way
[MATH=eng]Maxima(quad_qags(cspline(M),x,1,3))=sys(6.369565217391301,7.071637942785607*10^{-14},63,0,4,1)[/MATH]
Moreover, when I use Davide's, Gradiend.CD() I can get a function by numerically differentiating - but not its roots. This is a long time story, and I still can not figure out how to deal with this kind of problems in SMath.
Regards,
Radovan

When Sisyphus climbed to the top of a hill, they said: "Wrong boulder!"
#11 Posted: 1/11/2014 7:09:28 AM
You have to remove the suppression of charfun() (which I guess - if not bet - is still somewhere in your SMath sheet ;-)WroteThank you Martin,
Unfortunately, numerical integration in Maxima (quad* set of functions) will not work directly in SMath with this cubic spline.
Application and removal of type conversion functions like charfun() should be done in the translation process. This, however, is not yet implememted.
It might be a good idea to use the quadrature functions in Maxima for int() when numeric optimization is requested. This would, of course, require units preprocessing.
Martin KraskaPre-configured portable distribution of SMath Studio: https://en.smath.info/wiki/SMath%20with%20Plugins.ashx
#12 Posted: 1/11/2014 7:51:16 AM
WroteYou have to remove the suppression of charfun() (which I guess - if not bet - is still somewhere in your SMath sheet ;-)WroteThank you Martin,
Unfortunately, numerical integration in Maxima (quad* set of functions) will not work directly in SMath with this cubic spline.
Yes, you are right - I missed it
Regards,
Radovan
When Sisyphus climbed to the top of a hill, they said: "Wrong boulder!"
#13 Posted: 8/6/2015 1:26:11 AM
The latest Maxima 5.34.1 does not have numeric/interpol : tht's the first problem for all viewers.
Maxima cspline is an horrible monkey business probably incompatible with Smath, WHY ?
On the first count: Smath is not a 'scalar' system, only discrete.
Thus it might be impossible to built a scalar cspline that can be assigned as a function
as a function analytical up to the 2nd order derivative.
On the 2nd count: the former Maxima cspline is archaic in the displaying the segments,
just figure splining a data set of small 50 pairs. Again not exportable.
More confusing: Smath f(x) has linterp, ainterp [Akima spline], cinterp
these 3 are LOCAL interpolating functions, i.e: nothing else to do with
except populate data set for export.
_____________________________________________________
The Lagrange interpolation is totally useless. From a data set of length 'n' you can get
an nth order polynomial that will do exactly what your Lagrange interpolation does.
If your data set is like noisy or not so regular [they are always noisy or not very regular
from experimental sampling], the the polynomial fit can be or les order than the 'n' data.
Thus you benefit some smoothing. The polynomial fit need not be of integer monomials
x, x^2, x^3 ... the x's may be of decimal exponents, it may help the fit.
Polynomial fit is just few line of Smath simple coding.
A much, much, much more powerful fitter is the Padé rational fraction, in Mathcad 11, it works
by clicking the fingers. BTW, all [if not all] approximation of functions in computers
are Padé rational fractions [collected in Hart et al.]
jmgiraud@bell.net
Maxima cspline is an horrible monkey business probably incompatible with Smath, WHY ?
On the first count: Smath is not a 'scalar' system, only discrete.
Thus it might be impossible to built a scalar cspline that can be assigned as a function
as a function analytical up to the 2nd order derivative.
On the 2nd count: the former Maxima cspline is archaic in the displaying the segments,
just figure splining a data set of small 50 pairs. Again not exportable.
More confusing: Smath f(x) has linterp, ainterp [Akima spline], cinterp
these 3 are LOCAL interpolating functions, i.e: nothing else to do with
except populate data set for export.
_____________________________________________________
The Lagrange interpolation is totally useless. From a data set of length 'n' you can get
an nth order polynomial that will do exactly what your Lagrange interpolation does.
If your data set is like noisy or not so regular [they are always noisy or not very regular
from experimental sampling], the the polynomial fit can be or les order than the 'n' data.
Thus you benefit some smoothing. The polynomial fit need not be of integer monomials
x, x^2, x^3 ... the x's may be of decimal exponents, it may help the fit.
Polynomial fit is just few line of Smath simple coding.
A much, much, much more powerful fitter is the Padé rational fraction, in Mathcad 11, it works
by clicking the fingers. BTW, all [if not all] approximation of functions in computers
are Padé rational fractions [collected in Hart et al.]
jmgiraud@bell.net
1 Pages (13 items)
- New Posts
- No New Posts
