Here is a problem from a Matrix Analysis of Structures. I'm trying to solve by using the file provided here by [USERLINK]Alvaro Gavilan[/USERLINK], but for this exercise, the calculated stiffness matrix is singular.
Any ideas on how to solve and found the correct answers?



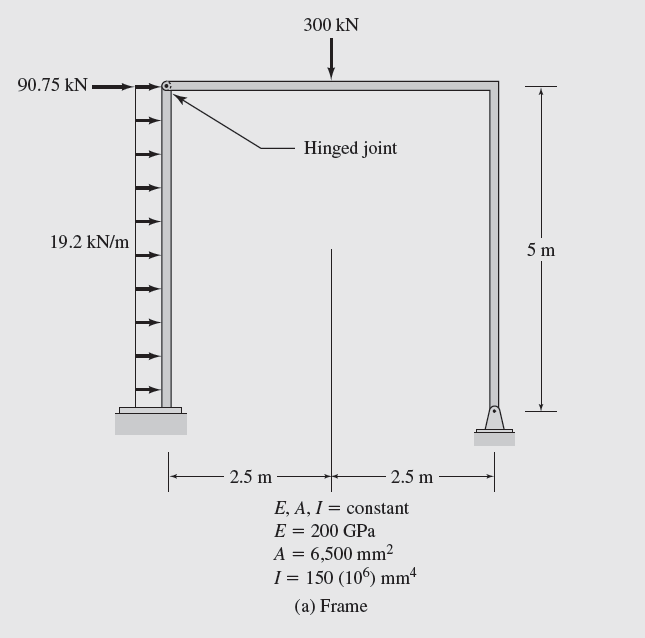
A Frame with internal releases.sm (248 KiB) downloaded 47 time(s).

Hola Oscar. Hope this helps: Please check example 7.1, page 353, from this book: Aslam_Kassimali_Matrix_Analysis_of_Structure. There are also an SI version of that book, but I don't have it.

Best regards.
Alvaro.

Wrote

Hola Oscar. Hope this helps: Please check example 7.1, page 353, from this book: Aslam_Kassimali_Matrix_Analysis_of_Structure. There are also an SI version of that book, but I don't have it.

Best regards.
Alvaro.

Gracias Alvaro,

I have precisely extracted this example from that book (SI Version) and I am trying to solve it using the file provided by Alvaro Gavilán, which he has successfully tested with other examples, but in this one, even though the loading conditions and the model for each bar are correct, it is not possible to calculate the system...

Solved...


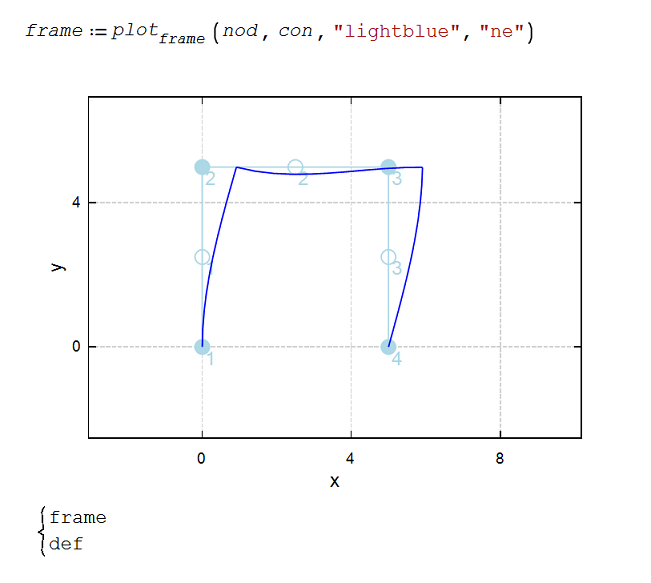
Custom FEM implementation.
I hope it would be useful for others:

A Frame with internal releases-SOLVED.sm (344 KiB) downloaded 56 time(s).

Best,
Oscar

Hola oscampo!

When singular matrices appear its probably due to a problem with hinged supports or connections. I verified the FE matrices and they are correct. I just changed some loads (that are corrected in your solved file) and then I changed two things:

1) Supports are always "rigid" when considering the member type. If we have a simple support for a frame, the beam that arrives to that support is a "rigid-rigid" member, we will just free the rotation in the constraints matrix (phi_z = 0).

2) When two members of a frame are connected with a hinge, one will be "rigid-hinge" and the other "rigid-rigid" (not "hinge-rigid"!). In these situations you have two rotations for the two beams that arrive at the hinge. To know the rotation corresponding to a certain beam, this has to be the "rigid-rigid" one.

A way of seeing this criteria is: we always prescribe rotations as unknowns, someone has to "withstand" those rotations (you can later "free" them with the constraints matrix), but if none of the elements can withstand that rotation, you will have a row (and column) full of zeros (zero stiffness) for that displacement in your K matrix.

Hope it is more clear!

Saludos,

Alvaro
A Frame with internal releases - v2.sm (256 KiB) downloaded 75 time(s).