I need an assistance to understand the situation with radians.

Yesterday I had the following discussion by e-mail:

Q: "Achtung! 1Hz=1rad/s. I believe the conversion between Herz and rad/s should use a factor of 2*Pi - that is one hertz, being a complete cycle or revolution per second, describes an angle of 2*Pi radians per second."

A: "I can explain the logic of the program: rad is dimensionless unit (1m/1m), so it is equal to 1. 1/s is a Hz."

Q: "What I' m suggesting is 1 Hz = 6.283185307179586476925286766559 rad/s"

A: "Problem is that by definition radian is 180deg/pi=1. But you propose to change the definition of the radian to 2pi - this is wrong."

Q: "The radian is an angle that spans an arc with the length equal with the radius. It is equal with 180°/Pi, as you mentioned. Please google "convert hertz to rad/s". The ratio is not 1, but 2*Pi."

---

Obviously this good man is right radian per second is not the same as 1/s. But what I do not understand is how it is possible that rad is dimensionless but its relation to a second is not that simple?

This question maybe stupid, but I'm not actually a mathematician so please forgive me for this

See also:

• https://math.stackexchange.com/questions/803955/why-radian-is-dimensionless
  
• https://www.wolframalpha.com/input/?i=1+rad+%2F+sec
  
• https://en.wikipedia.org/wiki/Radian

You can start by commenting that the dimension of a quantity is not the same as its units. For example, if I am going to buy paint and ask about its performance, I do not expect them to tell me that it yields three thousand reverse meters but three square meters per liter.



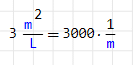
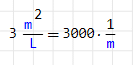
There are specific names for many dimensionless quantities, for instance you can see o lot of them here: https://en.wikipedia.org/wiki/Dimensionless_numbers_in_fluid_mechanics

Radian, degrees and "gradients" (***) are units for measure angles, which "loss" their dimension because are evaluated a quotient of two lengths.

Wrote

...
Q: "The radian is an angle that spans an arc with the length equal with the radius. It is equal with 180°/Pi, as you mentioned. Please google "convert hertz to rad/s". The ratio is not 1, but 2*Pi."
...

2*Pi*radius is for the entire circle length, not for the arc in the definition of radian.

Wrote

---

Obviously this good man is right radian per second is not the same as 1/s.
...

Nope. radian per second it is 1/s. In can't derive that from the animation, check the Official standard, from https://www.bipm.org/utils/common/pdf/si_brochure_8_en.pdf

Pages 119 - 120









Thus, SMath it's correct. Maybe what your friend needs to use is rpm, which have also a correct definition in SMath. It isn't in the BIPM bureau but can find it at NIST: https://physics.nist.gov/cuu/pdf/sp811.pdf





Finally you can tell to your friend that he can define new units in SMath, including undefined ones. Actually I do that for radians with 'Rad, to find the dimensions name from the units name here: https://en.smath.com/forum/yaf_postst17763_Dimensions-utility.aspx

Best regards.
Alvaro.

(***) : Almost all pocket calculators come with three options for measuring angles: deg, rad, and "grad." However I don't know anyone who uses "grad", which is dividing the circle by 100, not 360.

Hi. Perhaps I did not emphasize enough this important phrase on page 120 of the paper from the Bureau International des Poids et Mesures ( https://www.bipm.org/utils/common/pdf/si_brochure_8_en.pdf ) that may be enlightening to your friend:



Best regards.
Alvaro.

Wrote

Obviously this good man is right radian per second is not the same as 1/s. But what I do not understand is how it is possible that rad is dimensionless but its relation to a second is not that simple?
This question maybe stupid, but I'm not actually a mathematician so please forgive me for this

1rad/s reflects the speed of a flat angular motion [circular/elliptical motion]
More confusing is the numerical approximation of sin(x), cos(x) ...
The argument 'x' is rad.
The visitors may complete the X_Y plot attached.
Cheers ... Jean



Maths sin(deg) plot.sm (17 KiB) downloaded 28 time(s).

Thank you very much Razonar!

I've checked WolframAlpha and some converters online and I see that these tools understands the difference between Hz and rad/s.
F.e: https://www.wolframalpha.com/input/?i=1+rad+%2F+sec


See the line about Hz. Don't we need this in SMath Studio?

Many thanks for your time!

2*π rad/s [360°/s] => [1 revolution/s, 1 cycle/s, 1 period/s, 1 Hz]
By definition, 1 Hz is one period/s ... no matter the shape of the period.
As well, it may be represented by a bloc of data.

Wrote

See the line about Hz. Don't we need this in SMath Studio?
...

Hi. You can introduce definitions for cycle, rotation and revolution. In Wolfram alpha all are the same, but I think you might find this discussion interesting, where my choice for cycle is cycle:=1, not 2 Pi.

https://community.ptc.com/t5/PTC-Mathcad/Curve-fitting-units/m-p/499667

Naming rev or rot as 'rev:=2*Pi you can handle those values that appear in wolfram alpha.

From https://www.wolframalpha.com/input/?i=rot+%2Fs+in+rad%2Fs and similar:



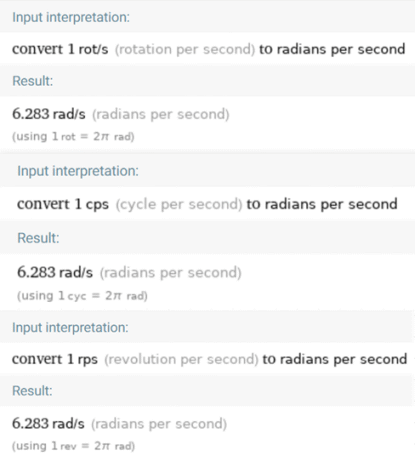
Finally, you can implement more complicate solutions, like this one in maple:



Best regards.
Alvaro.

Wrote

You can introduce definitions for cycle, rotation and revolution. In Wolfram alpha all are the same,

That's what I have explained above. At least, Wolfram conforms to the ancestors !