1 Pages (14 items)
Intersections Again - Messages
#1 Posted: 7/18/2020 9:08:11 AM
Hi All,
Trying to work out a universal way of getting the length of intersecting lines, easy when lines are level, but not so (for me) others.
The image below shows a lifting lug, the angle of action can be 0 deg to 150 deg for example. I need to know the length of the lines from the red circle to the outline, individually, then I can see the shortest length, this must be for all angles, effectively tracing the intersection point through the angles. I know I can use Pythagoras, but was hoping to use something like GPC, but this works only for polygons?
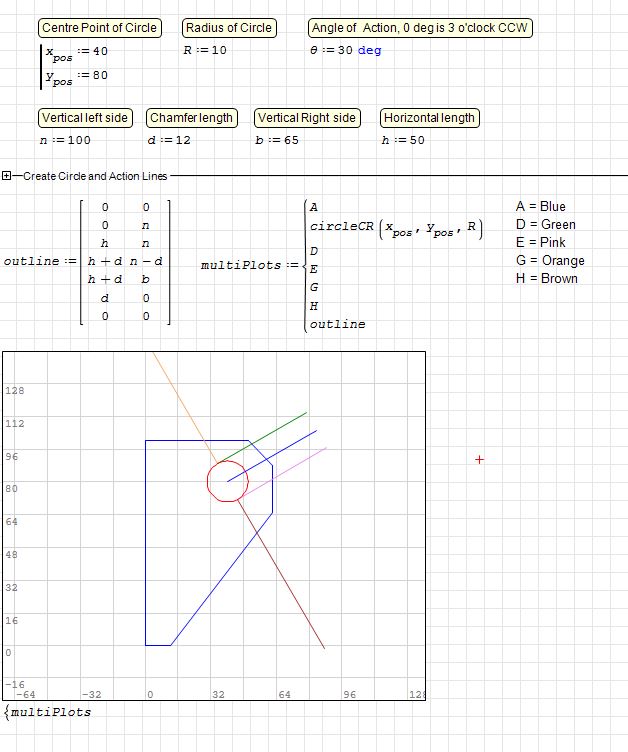
Lug Horizontal.sm (26.94 KiB) downloaded 682 time(s).
Trying to work out a universal way of getting the length of intersecting lines, easy when lines are level, but not so (for me) others.
The image below shows a lifting lug, the angle of action can be 0 deg to 150 deg for example. I need to know the length of the lines from the red circle to the outline, individually, then I can see the shortest length, this must be for all angles, effectively tracing the intersection point through the angles. I know I can use Pythagoras, but was hoping to use something like GPC, but this works only for polygons?
Lug Horizontal.sm (26.94 KiB) downloaded 682 time(s).
#2 Posted: 7/18/2020 1:42:58 PM
Try a short circle code.

1 users liked this post
frapuano 7/18/2020 4:52:00 PM
#3 Posted: 7/18/2020 7:09:52 PM
Anything helpful in there ?
Solve Circle Ellipse Strophoid NASA.sm (238.09 KiB) downloaded 734 time(s).
Solve Circle Ellipse Strophoid NASA.sm (238.09 KiB) downloaded 734 time(s).
#4 Posted: 7/19/2020 6:39:06 AM
Hi Jean,
I will have a look, I'm sure I can use something.
Thanks
I will have a look, I'm sure I can use something.
Thanks
#5 Posted: 7/20/2020 5:24:38 AM
ianlh, in your example it’s convenient to use the rotation matrix

Lug Horizontal1.sm (18.13 KiB) downloaded 676 time(s).

Lug Horizontal1.sm (18.13 KiB) downloaded 676 time(s).
1 users liked this post
Alvaro 7/21/2020 1:49:00 PM
#6 Posted: 7/20/2020 8:34:13 AM
Whereas the system is built scalar wrt θ
make it more convenient local at graph display.
Lug Horizontal_2.sm (22.51 KiB) downloaded 702 time(s).
make it more convenient local at graph display.
Lug Horizontal_2.sm (22.51 KiB) downloaded 702 time(s).
#7 Posted: 7/20/2020 1:46:20 PM
This provides the shortest distance from the segments of the polygon to the circle. However, the distance isn't really to the segment but to a line through the endpoints of the segment. There is no test if the normal to the line through c is between the vertices of the segment.
For the given geometry this works. For proof of strength this is only useful if a given force may act under any angle but the force doesn't depend on that angle.
Lug Horizontal_Kr.sm (31.23 KiB) downloaded 665 time(s).
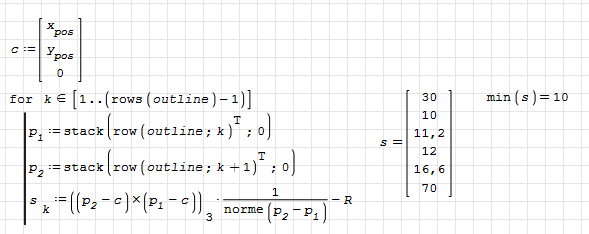
For the given geometry this works. For proof of strength this is only useful if a given force may act under any angle but the force doesn't depend on that angle.
Lug Horizontal_Kr.sm (31.23 KiB) downloaded 665 time(s).
Technische Mechanik mit SMath Studio: https://link.springer.com/book/10.1007/978-3-658-50592-9
#8 Posted: 7/21/2020 2:25:44 AM
WroteHi All,
Trying to work out a universal way of getting the length of intersecting lines, easy when lines are level, but not so (for me) others.
...
Hi. Your request it's about a complex computer graphic problem. This is a page for an undergraduated course: https://www.fing.edu.uy/inco/cursos/compgraf/
This paper have a pseudo code for solve partially your problem:
http://www.itseng.org/research/papers/topics/VLSI_Physical_Design_Automation/Physical_Verification/DRC/Geometric_Intersection_Problems/1979-Bentley.pdf
Hope that's helps.
Alvaro.
1 users liked this post
frapuano 7/21/2020 7:03:00 AM
#9 Posted: 7/21/2020 2:44:11 AM
Wroteianlh, in your example it’s convenient to use the rotation matrix
Lug Horizontal1.sm (18.13 KiB) downloaded 676 time(s).
Hi. This is what's actually do the Ber'f function:
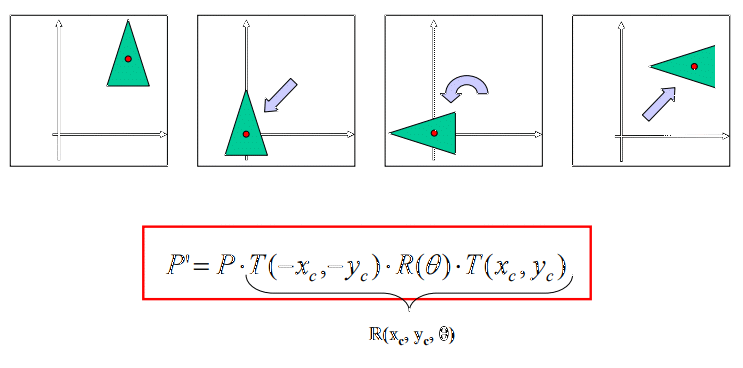
But notice that for use matrix multiplication for translations you must to use homogeneous coords ( http://elopez.fime.uanl.mx/@materias/732/@Tema%203%20-%20Transformaciones%202D.pdf page 15)
Best regards.
Alvaro.
2 users liked this post
#10 Posted: 7/21/2020 7:37:50 AM
Thank you, Razonar.Aapplying homogeneous coordinates helps automate the process.
Variant with homogeneous coordinates

Lug Horizontal3.sm (17.83 KiB) downloaded 708 time(s).
Variant with homogeneous coordinates

Lug Horizontal3.sm (17.83 KiB) downloaded 708 time(s).
#11 Posted: 7/21/2020 2:15:57 PM
Wrote...
Variant with homogeneous coordinates ...
Another variant.
Lug Horizontal4.sm (34.62 KiB) downloaded 702 time(s).
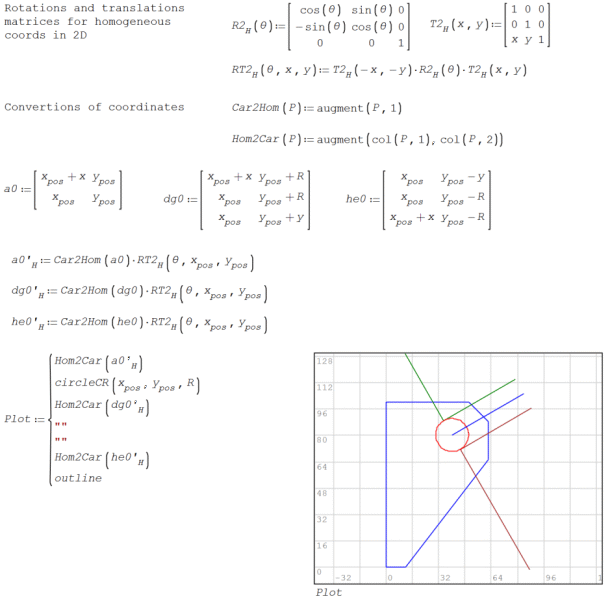
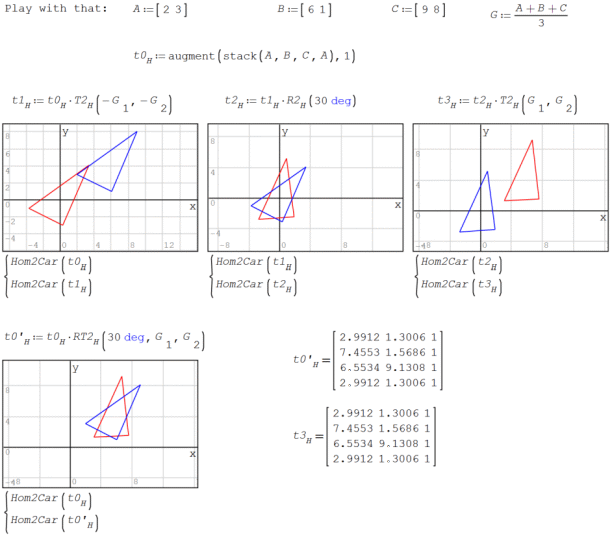
Homogeneous coordinates are helpful in projective geometry and conics and quadrics. For instance, preserve the duality, because you can use line coordinates ( https://en.wikipedia.org/wiki/Line_coordinates ).
I try to modify for use that in https://en.smath.com/forum/yaf_postst17357_Conics.aspx but can't found a close end. This is my atemp for the dual of a conic, it's envelope:
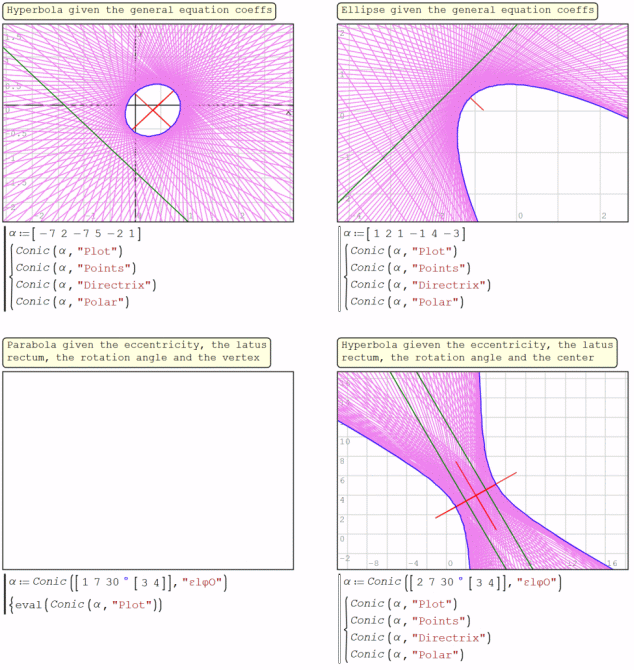
Best regards.
Alvaro
2 users liked this post
#12 Posted: 7/24/2020 9:27:21 AM
#13 Posted: 7/27/2020 12:37:33 AM
Hi Ber. That's not science, that's art. Maybe you can find this book interesting: Modern Robotics.
At page 608 in the pdf, for example:


The notation isn't the best, but it can be converted to a general Rotations and translations for the forward kinematics of a robot.
Best regards.
Alvaro.
At page 608 in the pdf, for example:


The notation isn't the best, but it can be converted to a general Rotations and translations for the forward kinematics of a robot.
Best regards.
Alvaro.
2 users liked this post
#14 Posted: 7/27/2020 5:31:15 AM
Hello Razonar. "Modern Robotics" book
sparked my big interest. Thank you for the link.
sparked my big interest. Thank you for the link.
1 Pages (14 items)
- New Posts
- No New Posts


