1 Pages (4 items)
"Result is above of max. allowed positive Number" error - "Result is above of max. allowed positive Number" error during a programming - Messages
#1 Posted: 2/2/2017 1:26:14 PM
Dear Masters,
I've got the error message, "'Result is above of max. allowed positive Number", frequently during programming.
Please, check it.
File not found.File not found.File not found.
I've got the error message, "'Result is above of max. allowed positive Number", frequently during programming.
Please, check it.
File not found.File not found.File not found.
#2 Posted: 2/2/2017 2:59:39 PM
#3 Posted: 2/2/2017 3:18:53 PM
So you have some weird stuff going on here. All of your assignments seem to be optimized for symbolic evaluation.
What I did was take your first example program and rewrote it. I got the same error. I replaced the constant 'e' with the exp function in the second version of the program. That seemed to fix it.
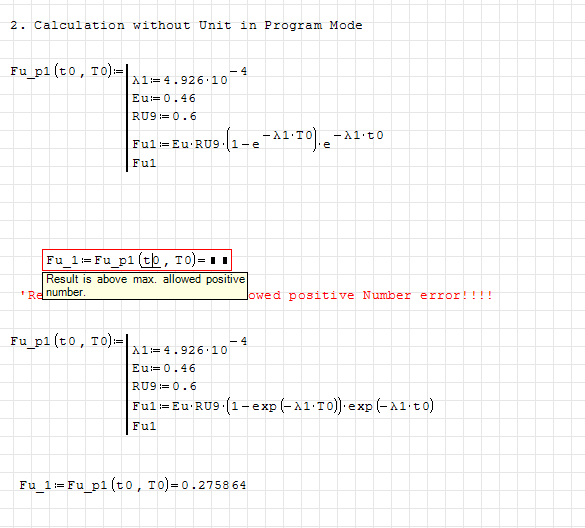
I found that rewriting the program and replacing 'e' with the function exp() seemed to fix it. In the original program I tried replacing 'e' with exp() and still got an error. I'm wondering if you copy/pasted the assignments from above into the program. Those were optimized for symbolic calculation. I found that using eval() within the program fixed the problem as shown below. Even when I replaced 'e' with exp() in your original program, I had to use eval(). That's why i think the symbolic optimation got "stuck" in your assignments within the program.
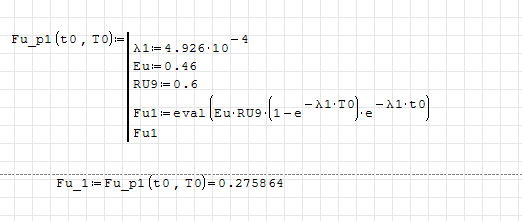
What I did was take your first example program and rewrote it. I got the same error. I replaced the constant 'e' with the exp function in the second version of the program. That seemed to fix it.

I found that rewriting the program and replacing 'e' with the function exp() seemed to fix it. In the original program I tried replacing 'e' with exp() and still got an error. I'm wondering if you copy/pasted the assignments from above into the program. Those were optimized for symbolic calculation. I found that using eval() within the program fixed the problem as shown below. Even when I replaced 'e' with exp() in your original program, I had to use eval(). That's why i think the symbolic optimation got "stuck" in your assignments within the program.
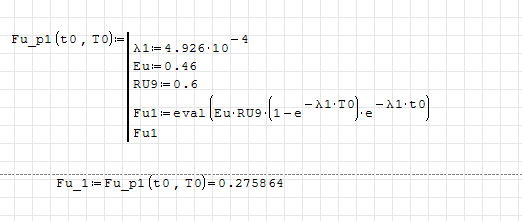
Feel free to join the SMath Studio Users Discord Channel: https://discord.gg/PayZpJW
#4 Posted: 2/2/2017 10:57:44 PM
WroteI found that rewriting the program and replacing 'e' with the function exp() seemed to fix it.
In theory, exp(,) is more accurate as it involves only ONE
numerical approximation vs e that needs TWO numerical
approximations. However, one vs the other is immaterial
wrt the result, only 15 decimals are conserved from 21.
Your program is not correct, conserve the "yellow offer"
exp(-x) has no limit value in 'x'
exp(x) is limited to "xmax=709"
1 Pages (4 items)
- New Posts
- No New Posts
