Hi,

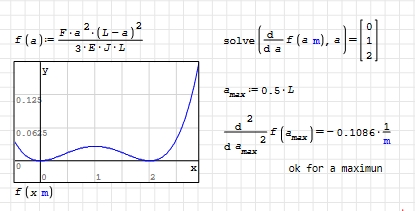
it's a rather simple thing but somehow I'm stuck. Consider a simply supported beam with concentrated force. Let's say that we don't know that deflection will be maximum with force acting in the middle of the beam. How can I find the maximum deflection in SMath ? Of course I have all the data and the formula for deflection of this beam:



But I assume that the distance a is not known and all values in the range of a=0 to a=L should be checked or maximum of the function should be found.

I've also attached the .sm file with data shown in the picture above.

Thanks in advance for you help.


Beam max deflection.sm (35 KiB) downloaded 33 time(s).

Hi. This?


Beam max deflection.sm (38 KiB) downloaded 39 time(s).

Best regards.
Alvaro.

You don't say much about the project, let's invent something.

Beam max deflection [1].sm (48 KiB) downloaded 37 time(s).

Wrote

Hi. This?


Beam max deflection.sm (38 KiB) downloaded 39 time(s).

Best regards.
Alvaro.

Thank you very much. I just wonder why the plot has a concave part in the middle instead of being a regular parabola.

Wrote

You don't say much about the project, let's invent something.

This project is nothing special. I'm just analyzing a simple case because I wonder how such thing can be done in SMath. Thank you for help.

Wrote

I just wonder why the plot has a concave part in the middle instead of being a regular parabola.

Parabola will be concave as well.
Parabola will suppose not anchored end points.
Make it as you wish.
Cheers ... Jean

Wrote

Thank you very much. I just wonder why the plot has a concave part in the middle instead of being a regular parabola.

Function has to to plot only between 0-L.
You have to limit otherwise it will try to plot for all numbers.
In case you don't limit, that will create the plot which Razonar provided.
Which is not wrong but over-plotted. No need to plot outside of 0-L.
You need to plot with units eliminated of course.

Since F is considered positive directioned, f(x) shall be plot as concave.
To plot as convex, try to reverse direction of F by multiplying it with -1.



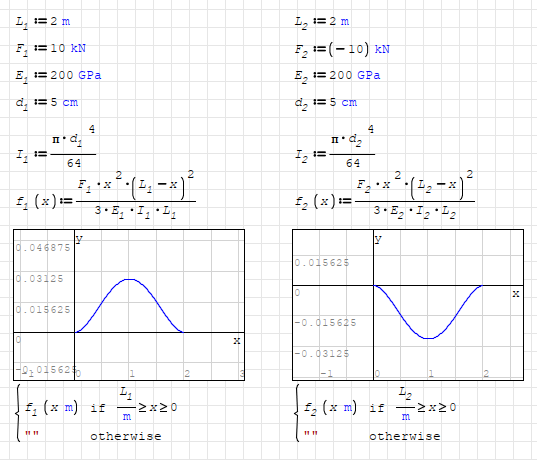
Or simply reverse the f(x) by multiplying it with -1.



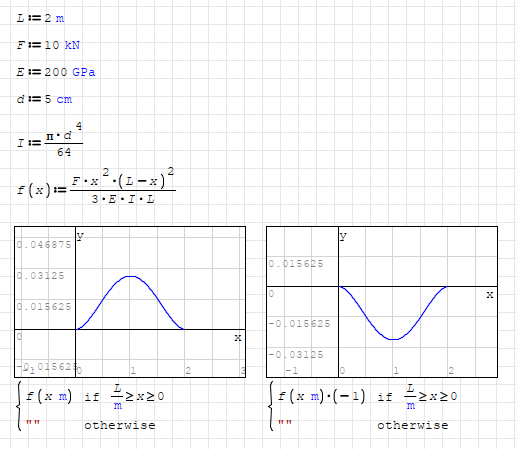
Regards

The formula given by the topic starter probably wasn't the elastic line but the dependency of the maximum deflection from the point of load application, i.e. a reference solution.

To find the same value with SMath you need to solve for the elastic line and then find the maximum.

If the formula was meant to be the elastic line, it would not meet the boundary condition (simply supported beam)

Wrote

Let's say that we don't know that deflection will be maximum with force acting in the middle of the beam. How can I find the maximum deflection in SMath?

By the way, if we return to your original question;
Maximum or minimum peak point of a function is differentiate of that function.
You can find it with solvers like solve(), roots() or FindRoot().
First plot the function as it is, it will give you an idea for its maximum or minimum.
Just choose a fine starting guess for solvers, they will deal the rest.
Maximum deflection shall be the result of function by using the length which solvers found.

Regards

"Function has to to plot only between 0-L."

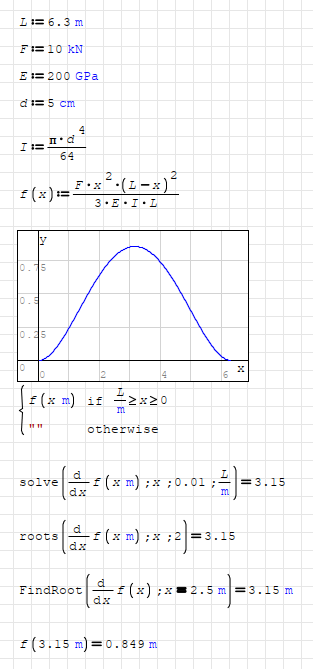
I agree with overlord. The deflection function of the
beam f(x) is valid only in the area from 0 to L.

Here is a solution for the elastic line of a simply supported beam from scratch.

I don't know what the formula in the topic opening post is meant to be.

Worksheet6.sm (47 KiB) downloaded 35 time(s).

Thank you all for your replies. The formula attached to my first post is from a book (something like a Polish equivalent of Roark’s Formulas for Stress and Strain). It can be used to obtain the deflection at the point of force application.

I was trying to use the root function as well but with no success. So the initial guess is necessary in this case ? I thought that I can use some predefined function to find local maximum in the specified range of arguments (a=0 to a=L in this case) without the need to do the initial guess.

Wrote

I was trying to use the root function as well but with no success. So the initial guess is necessary in this case ?

roots() and FindRoot() needs a starting point, a guess value to find the solution.
solve() doesn't need that "guess", it can find all solutions in the depicted range.
However, solve() shall need an assigned range if solution is not between {-20,20} or what range is chosen in options menu.

Regards

Wrote

Thank you all for your replies. The formula attached to my first post is from a book (something like a Polish equivalent of Roark’s Formulas for Stress and Strain). It can be used to obtain the deflection at the point of force application.

Make that formula produce the graph as function of the point of applied force.
From there, the suite will come easily [Min/Max ...]. No Graph=NO suite.
As you can see, there is a missing link in your formula.
Cheers ... Jean

Beam max deflection.sm (52 KiB) downloaded 44 time(s).

1. This document implements Martin formula.
2. From there => location of max deflection and value.
Is that what you were looking for ? ... Jean

Page13 Martin.sm (50 KiB) downloaded 38 time(s).

Hi. Some examples about how to solve beams with rk solver, shooting method and boundary value problem ode solver.

beam.pdf (728 KiB) downloaded 67 time(s).
beam.sm (728 KiB) downloaded 65 time(s).

Best regards.
Alvaro.