Many Greetings
Has anyone made a function in Smath for factoring a number into a continued fraction, similar to making the symbolic function K confrac in MathCad?! Where K represents a fractional decimal number, as in the example in the attached image.

Here is a sample for your question.

Regards

confrac.sm (18 KiB) downloaded 31 time(s).

Wrote

Has anyone made a function in Smath for factoring a number into a continued fraction ...

If your data set is clean from published data or collected discrete
it will convert data in scalar function, compliant to scalar derivative.
Continued fraction is the candidate ...atmosphere 0...100 km
see Ralph Karmichael ISA ... module coded in Smath.
More in IAPWS.

Long word short, Jean doesn't have the answer to your question.
This is how he achieved 1800 posts, 18.47% of all smath forum posts.
Replying with totally ridiculous and unuseful posts.

Below is a function to sum matrix of confrac().

Regards

Wrote

Here is a sample for your question ...

Thank you very much for the answer. I arrived at a very similar relation, but which did not work because I omitted to declare the function variable at the beginning of the program in the right member of the definition relation. Using MathCad quite often (where the variable / variables of the function are automatically declared only by mentioning them in the left member of the definition relation) I tend to apply the same rules in Smath. Thank you again.
Greetings.

Wrote

Has anyone made a function in Smath for factoring a number into a continued fraction ...

Yes, in most advanced profitable.
Best to save a copy before experimenting
Jean.

ConfracNUMBER Copy.sm (46 KiB) downloaded 22 time(s).

@uni: The advantage of the relationship is that it takes up little space in the worksheet. The disadvantage of designing such a relationship is that the component functions (convert, confrac, vector) are not predefined anywhere in the program's toolbars (at least not in the version I have). Maybe in newer versions there are predefined functions for these functions.
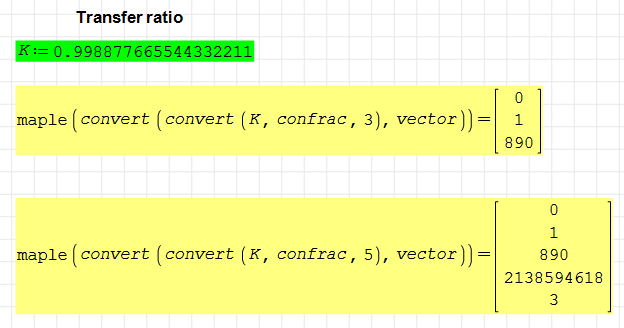
@Jean Giraud: As a former engineer (currently retired), I base it on practice, simplicity and efficiency. Therefore, in my applications, I don't need anything else than a vector of the decomposition of a decimal fraction into a continued fraction. I used this function (confrac) to calculate the number of teeth of several pairs of gear wheels, in order to obtain a certain transfer ratio K.
On another note, everything you have presented here probably has multiple applications, depending on the field of interest. So thank you all.
Greetings.