Is this a bug or calculation limitation?

Regards

euler.sm (10 KiB) downloaded 27 time(s).

Hi overlord. It's a numerical round-off issue. For example you can get the same issue in excel, with more or less same values.

round-off-error.pdf (204 KiB) downloaded 31 time(s).

Some few notes:
- You can estimate the error for floating point arithmetic. For that you can check almost any numerical methods undergraduate page or book. Also can check this article in the wikipedia: Loss of significance.
- The primary way is just know the "exact" value and compare it the obtained. That's one big application of your code for the extended arithmetic.
- One reason for use books like Numerical Recipes in C and similar is that one assume that the algorithms in the book are optimized for minimize those errors. For instance, in the order of the arithmetic.
- This kind of errors make more pedagogical to study first numerical algorithms for integration and then derivatives, and sometimes the function evaluation. Here an example of the Numerical Recipes in C index



Best regards.
Alvaro.

Wrote

Hi overlord. It's a numerical round-off issue. For example you can get the same issue in excel, with more or less same values.

Best regards.
Alvaro.

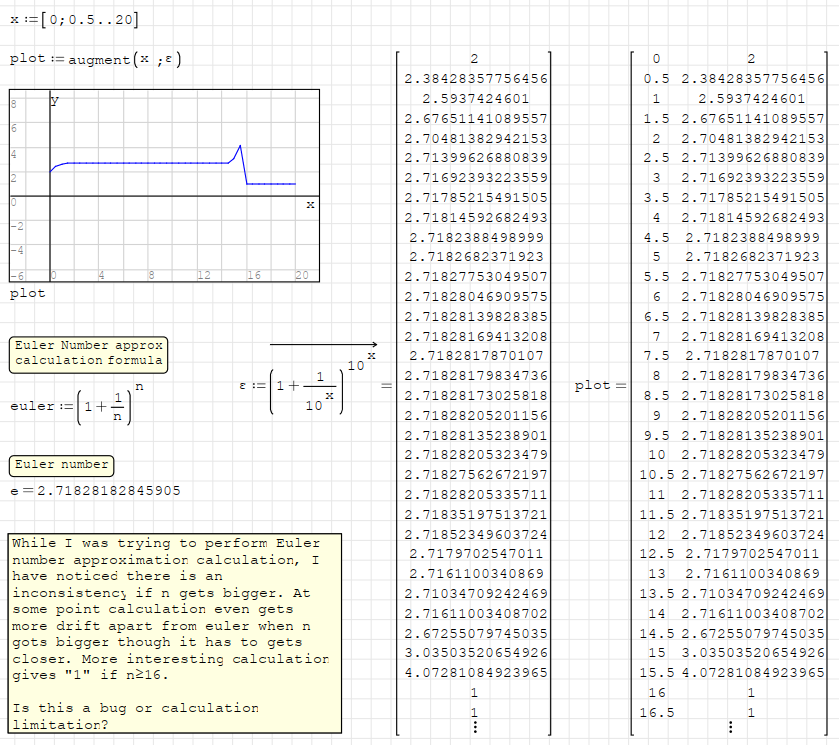
Thank you Alvaro,

I had only checked this formula only with wolframalpha website.
On it, there were no issues, everything was smooth.
Then I tried it with SMath and get those results.
After your post I calculated with Mathcad and Mathematica.
Results are worse over them. Mathematica can not calculate after exp(7).
On Mathcad results have same spike and they are settled on 1 after it.
So this is basically a limitation. No need to investigate further.

Best regards to you Razonar,
Thanks again.