1 Pages (12 items)
Integral with measurement units - Messages
#1 Posted: 1/8/2013 5:17:32 AM
Hello everybody.
I'm using a definite integral of a function with a variable defined with measurement unit.
When I try to obtain the value of the integral I get an error saying that the variable is not defined.
I tried removing the measurement unit dividing the variable by the measurement unit itself but I get the same error.
Thank you very much for any suggestion.
I'm using a definite integral of a function with a variable defined with measurement unit.
When I try to obtain the value of the integral I get an error saying that the variable is not defined.
I tried removing the measurement unit dividing the variable by the measurement unit itself but I get the same error.
Thank you very much for any suggestion.
#2 Posted: 1/8/2013 9:07:20 AM
Hello,
I would generally discourage using units in solving definite integrals by SMath. This method was not meant to be used with units, AFAIK. On the other hand, this might be a source of mistakes and confusions.
Regards,
Radovan
I would generally discourage using units in solving definite integrals by SMath. This method was not meant to be used with units, AFAIK. On the other hand, this might be a source of mistakes and confusions.
Regards,
Radovan
When Sisyphus climbed to the top of a hill, they said: "Wrong boulder!"
#3 Posted: 1/8/2013 12:13:48 PM
omorr,
this time I disagree with you. A definite integral of a physical quantity is perfectly defined and has strong meaning.
No mistakes should be expected in the undestanding of such integrals.
I can understand that for technical reasons this may be not (yet) implemented on SMath, but in that case it would be much better to prevent the user, raising an error if a definite integral is used with units. Actual behavior is wrong.
For example I defined
V0=20 m/s
t1=0 s
t2=10 s
The definite integral of V0*dt with t from t1 to t2 is the space traveled at the constant V0 speed in t2-t1=10s. I should get meters, instead the result of the integral is still a speed.
May be I'm a bit oversimplifying, but the resulting unit shall simply be the unit of the function multiplied the unit of the boundaries (which shall be the same). It should be not too hard to be implemented.
Thanks :-)
Andrea
this time I disagree with you. A definite integral of a physical quantity is perfectly defined and has strong meaning.
No mistakes should be expected in the undestanding of such integrals.
I can understand that for technical reasons this may be not (yet) implemented on SMath, but in that case it would be much better to prevent the user, raising an error if a definite integral is used with units. Actual behavior is wrong.
For example I defined
V0=20 m/s
t1=0 s
t2=10 s
The definite integral of V0*dt with t from t1 to t2 is the space traveled at the constant V0 speed in t2-t1=10s. I should get meters, instead the result of the integral is still a speed.
May be I'm a bit oversimplifying, but the resulting unit shall simply be the unit of the function multiplied the unit of the boundaries (which shall be the same). It should be not too hard to be implemented.
Thanks :-)
Andrea
#4 Posted: 1/8/2013 12:59:36 PM
Thank you very much for your answer,
I've attached a file that's explaining the error that I get.
resource1.sm (13.04 KiB) downloaded 791 time(s).
I've attached a file that's explaining the error that I get.
resource1.sm (13.04 KiB) downloaded 791 time(s).
#5 Posted: 1/8/2013 1:14:02 PM
#6 Posted: 1/8/2013 2:42:35 PM
Good point:
If your function involves units you must specify units on the independent variables when calling the function.
Edit:
Anyway on my sample the integral seems problematic dealing with units, since it should return square meters.
Edit2:
Sorry for the confussion, the integral works fine here!
I wanted to assign units to the result taking into account the geometrical interpretation of line integral, similarly Callmeishmael referred to units for the physical meaning of velocity.
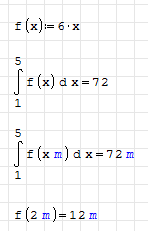
If your function involves units you must specify units on the independent variables when calling the function.
Edit:
Anyway on my sample the integral seems problematic dealing with units, since it should return square meters.
Edit2:
Sorry for the confussion, the integral works fine here!
I wanted to assign units to the result taking into account the geometrical interpretation of line integral, similarly Callmeishmael referred to units for the physical meaning of velocity.
1 users liked this post
Davide Carpi 1/9/2013 8:44:00 AM
#7 Posted: 1/9/2013 5:03:04 AM
Thank you very much for your suggestions: now the formula is working correctly.
#8 Posted: 11/12/2014 3:02:20 PM
WroteGood point:
If your function involves units you must specify units on the independent variables when calling the function.
I don't understand. If you have a constant power dissipation of 1 W for 1 second, you will consume 1 J of energy. To write this in integral form: [see attached image]
int(1 W, dt, 1 sec, 2 sec) should equal 1 W * (2 sec - 1 sec) = 1 J
So why can't we use units in the limits of the integral?
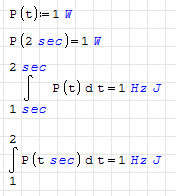
#9 Posted: 11/12/2014 4:14:37 PM
Problems with the integrals are known. You can find more details in the Interactive SMath Handbook (author Martin Kraska).
At the moment, your problem can be solved as in attached figure
[albumimg]364[/albumimg]
sergio
At the moment, your problem can be solved as in attached figure
[albumimg]364[/albumimg]
sergio
#10 Posted: 11/12/2014 5:13:44 PM
So you're basically removing the units before the integral and then re-adding them after it's done? What does LE stand for and why is it blue like a unit for you? It's not for me.
#11 Posted: 11/13/2014 3:32:05 AM
#12 Posted: 11/13/2014 12:33:13 PM
..assuming you have the Maxima plugin installed and Maxima installed?
1 Pages (12 items)
- New Posts
- No New Posts

![SMath Studio - [resource1.sm].png](/en-US/files/Download/LFMAxQ/SMath-Studio---[resource1.sm].png)
