Hi,

I have come across some problems while using polyroots. I am solving a cubic polynomial and I have a problem where polyroots rearranges the solutions when I make slight adjustments to the input.

How does polyroots arrange the solutions?

Best regards,

Sorry, I forgot to upload.

Hope you can make sence of the attached sheet and the "problem" I am faced with.

Best regards,

cubic.sm (77 KiB) downloaded 53 time(s).

Wrote

I have come across some problems while using polyroots. I am solving a cubic polynomial and I have a problem where polyroots rearranges the solutions when I make slight adjustments to the input.
How does polyroots arrange the solutions?

Work in progress ... hope it can be automated, be patient.
Jean

cubic.sm (106 KiB) downloaded 28 time(s).

Wrote

Sorry, I forgot to upload.

Hope you can make sence of the attached sheet and the "problem" I am faced with.

Best regards,

cubic.sm (77 KiB) downloaded 53 time(s).

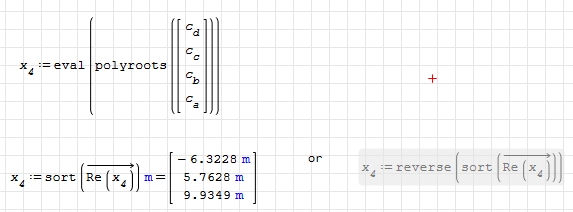
Usually polynomial roots sorting can't be done, just because they are complex numbers in the general case, and you can't define an order relation there. But forcing to get only reals, you can use sort() or reverse(sort()). The same could be done with the solve code at the end of your document.



Best regards.
Alvaro.

... the project is now automated except as explained in green.
That inconvenience was not solved in Mathcad either.
Up to you to sanity at sol_1, sol_2 if they follow upstream
parameters and so on ... [you are the Expert in what I'm not].
Please, come back for more or better presentation.
Cheers ... Jean

cubic Polyroots Automated.sm (94 KiB) downloaded 40 time(s).

... as long as sol_1 will have missing term 'x',
easy to force Polyroots to complete full automated project.

cubic Polyroots Automated.sm (96 KiB) downloaded 27 time(s).

Wrote

... as long as sol_1 will have missing term 'x',
easy to force Polyroots to complete full automated project.

... slight refresh ... Golden ratio added.

cubic Polyroots Automated.sm (108 KiB) downloaded 32 time(s).

Wrote

Usually polynomial roots sorting can't be done, just because they are complex numbers in the general case, and you can't define an order relation there. But forcing to get only reals, you can use sort() or reverse(sort()). The same could be done with the solve code at the end of your document.



Best regards.
Alvaro.

Alvaro,

Thank you. Did not think about sort(), that would do the trick.

Is it possible to extract solution(s) from the vector that satisfies 0≤x≤L?

Best regards,

Wrote

... the project is now automated except as explained in green.
That inconvenience was not solved in Mathcad either.
Up to you to sanity at sol_1, sol_2 if they follow upstream
parameters and so on ... [you are the Expert in what I'm not].
Please, come back for more or better presentation.
Cheers ... Jean

cubic Polyroots Automated.sm (94 KiB) downloaded 40 time(s).

Jean,

Thank you for the input. I dont have the Maple Tools plugin, so I cant see all the results from your sheet.

Alvaro's suggestion to use sort() helps me "hardcode" the desired solution, but I didnt quite understand why polyroots() doesnt sort its solutions. Any insight on that matter?

Best regards

Wrote

Thank you for the input. I dont have the Maple Tools plugin, so I cant see all the results from your sheet.

Alvaro's suggestion to use sort() helps me "hardcode" the desired solution, but I didn't quite understand why polyroots() doesn't sort its solutions. Any insight on that matter?

In your project, Polyroots does nothing except allowing export the solutions.
Which solutions [sol_1(x), sol_2(x)] conclude your design inputs.
Smath w/o Maple is not intended Smath.
Some advanced projects resume w/o Maple.
Attached for checking down to Golden ratio.

cubic Polyroots REMOVED.sm (86 KiB) downloaded 31 time(s).

Wrote

...
Is it possible to extract solution(s) from the vector that satisfies 0≤x≤L?

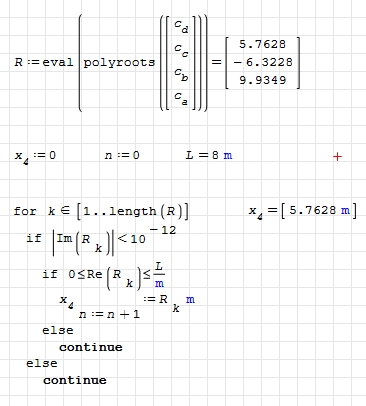
Hi. Sure. For instance can use a for loop, like in the attached.



cubic.sm (82 KiB) downloaded 20 time(s).

Wrote

...
but I didn't quite understand why polyroots() doesn't sort its solutions. Any insight on that matter?

The problem is that the complexes cannot be ordered, so there is no standard about how to present the results.

However, since the roots of a polynomial are usually calculated as the eigenvalues of the companion matrix, and numerical procedures usually order these eigenvalues according to their magnitude, which is a real number, since it does have applications to keep the large eigenvalues and neglect the small ones, perhaps that is the order in which the roots appear in polyroots (): ordered by their complex magnitude, but I can't be sure, since I don't know the SMath routine for its calculation.

Best regards.
Alvaro.

Wrote

I didnt quite understand why polyroots() doesnt sort its solutions. Any insight on that matter?

Polyroots obey the rules from libraries [maybe Smath is NAG ?]
It is incomplete as it can not calculate complex vector.
Visit Samples just posted for your tool box.
I guess Norway not yet green like here !
Take care ... Jean

Wrote

Polyroots obey the rules from libraries [maybe Smath is NAG ?]
It is incomplete as it can not calculate complex vector.
Visit Samples just posted for your tool box.
I guess Norway not yet green like here !
Take care ... Jean

Jean,
Sometimes I feel like you are talking over my head and overestimate my level of understanding the maths involved in my (structural engineering) projects. I guess thats partly why I like this forum, no matter what thread I read I feel like there’s new things to learn.

The winter is still going strong over here, at least when you get some distance to the coast and fjords. We had a wonderful day skiing today.

Best regards,

Wrote

Wrote

Thank you for the input. I dont have the Maple Tools plugin, so I cant see all the results from your sheet.

Alvaro's suggestion to use sort() helps me "hardcode" the desired solution, but I didn't quite understand why polyroots() doesn't sort its solutions. Any insight on that matter?

In your project, Polyroots does nothing except allowing export the solutions.
Which solutions [sol_1(x), sol_2(x)] conclude your design inputs.
Smath w/o Maple is not intended Smath.
Some advanced projects resume w/o Maple.
Attached for checking down to Golden ratio.

cubic Polyroots REMOVED.sm (86 KiB) downloaded 31 time(s).

Jean,

Very interesting example searching for max/min.
In my project, I am searcing for max/min of the function w(x), by finding the roots of it's first derivative θ(x).

Best regards,

Wrote

The problem is that the complexes cannot be ordered, so there is no standard about how to present the results.

However, since the roots of a polynomial are usually calculated as the eigenvalues of the companion matrix, and numerical procedures usually order these eigenvalues according to their magnitude, which is a real number, since it does have applications to keep the large eigenvalues and neglect the small ones, perhaps that is the order in which the roots appear in polyroots (): ordered by their complex magnitude, but I can't be sure, since I don't know the SMath routine for its calculation.

Best regards.
Alvaro.

Alvaro,

Thank you for the beatiful way of filtering out the relevant roots. I have some questions.
1. Why do you use length(R) rather than rows(R) to determine the upper limit of the range?
2. Is abs(Im(el(R,k)))<10^{-12} the only way of determining if a number is non-complex ie. has no imaginary part (I dont know the correct term for such a number, or is it Reals?)
3. Would you trust polyroots() over someting like the cubic solver in the attached sheet? I want to use code that finds the solutions symbolically rather than numerically.
4. I should probably define a function that finds the roots of a polynomial that are within a range if I want to to this several times within the same sheet?

Best regards,

cubicroots.sm (9 KiB) downloaded 33 time(s).

Wrote

3. Would you trust polyroots() over something like the cubic solver in the attached sheet? I want to use code that finds the solutions symbolically rather than numerically.
4. I should probably define a function that finds the roots of a polynomial that are within a range if I want to to this several times within the same sheet?

3. Your cubic is incorrect vs the conventional attached and Polyroots.
4. That's another story but can be done from scanning trough the various
vectors you want to explore. Possibly plot/stack all explorations.
More and + interesting ... Jean

cubicroots [sanity check].sm (37 KiB) downloaded 39 time(s).

... here is a brute force plot scanner/explorer
Design the 'a' vectors at will for best expected.
Cheers ... Jean

cubicroots [Brute Force Scanner].sm (21 KiB) downloaded 37 time(s).

Wrote

1. Why do you use length(R) rather than rows(R) to determine the upper limit of the range?
2. Is abs(Im(el(R,k)))<10^{-12} the only way of determining if a number is non-complex ie. has no imaginary part (I dont know the correct term for such a number, or is it Reals?)
3. Would you trust polyroots() over someting like the cubic solver in the attached sheet? I want to use code that finds the solutions symbolically rather than numerically.
4. I should probably define a function that finds the roots of a polynomial that are within a range if I want to to this several times within the same sheet?

1. True Vectors are column vectors, the expression "row vector" actually means nothing. But ... columns don't look good. Using length() instead rows() I can use row or column vectors in my procedures.

2. No, it isn't. But routines in polyroots() usually introduce some imaginary parts in roots because roundoff errors evaluating the discriminant of the polynomial equation. The question Im(R.k)=0 could look better, but for numerical methods it's impractical.

3. I don't know the internals of SMath polyroots(), but I'm pretty sure that can't handle symbolic values. And I'm pretty sure also that an application in civil engineering with symbolic expressions for cubic polynomials roots requires a very powerful symbolic kernel, and SMath isn't at that stage right now.

4. Sure, first use your cubic, which works well and it's equivalent to polyroots(reverse(stack(a,b,c,d)) and then define another for take only roots in the desired interval. Notice that in my procedure I assign x.4[n:=n+1] to R[k] but it's more correct assign to Re(R[k]).

Best regards.
Alvaro.

Wrote

3. Would you trust polyroots() over something like the cubic solver in the attached sheet? I want to use code that finds the solutions symbolically rather than numerically.
4. I should probably define a function that finds the roots of a polynomial that are within a range if I want to to this several times within the same sheet?

........................
2. The cubic module as constructed is same as polyroots with the nuance.
cubic takes the vector [3] ... polyroots takes [4]
The nuance is that if the last v[4 is not '1' then the plot is scaled
to that factor... otherwise: if v[4 is 1 same roots.
3. At this point of your project, you have reduced the long arguments
by sol_1(x), sol_2(x). At this next point, if you want either/both functions
to pass a cubic polynomial through, you define a set of 4 points that
make sense wrt the nature of your expectation, then solve for the coefficients of the cubic polynomial.
Doing so, no needs for cubic, neither polyroots
neither for symbolic of any kind, neither partial fraction expansion.
................
The attached linfit module does all that, no sweat/quick,
infinitely re-usable for each set of new experimental XY
What it returns is simply your 4 set of the resulting design values
that produce your experimental demand
BTW, linfit is unlimited in the order of polynomial fit.
Cheers ... Jean.

Cubic solver QUICK Explorer.sm (49 KiB) downloaded 39 time(s).

Wrote

1. True Vectors are column vectors, the expression "row vector" actually means nothing. But ... columns don't look good. Using length() instead rows() I can use row or column vectors in my procedures.

2. No, it isn't. But routines in polyroots() usually introduce some imaginary parts in roots because roundoff errors evaluating the discriminant of the polynomial equation. The question Im(R.k)=0 could look better, but for numerical methods it's impractical.

3. I don't know the internals of SMath polyroots(), but I'm pretty sure that can't handle symbolic values. And I'm pretty sure also that an application in civil engineering with symbolic expressions for cubic polynomials roots requires a very powerful symbolic kernel, and SMath isn't at that stage right now.

4. Sure, first use your cubic, which works well and it's equivalent to polyroots(reverse(stack(a,b,c,d)) and then define another for take only roots in the desired interval. Notice that in my procedure I assign x.4[n:=n+1] to R[k] but it's more correct assign to Re(R[k]).

Best regards.
Alvaro.

Thanks for the explanations.

Re 3, I think I worded myself poorly. Numeric evaluation of algebraic equations are fine by me, I just didnt want to code with a numeric tool like solve () that just checks all the values wihtin it's range to find the roots.

I guess there is no reason to use my own code to solve polynomials when SMath has polyroots. The cubic solver from my last post was something I made before I discovered polyroots.

Re 4, does this look like what you would have made to serve this purpose?



Best regards,