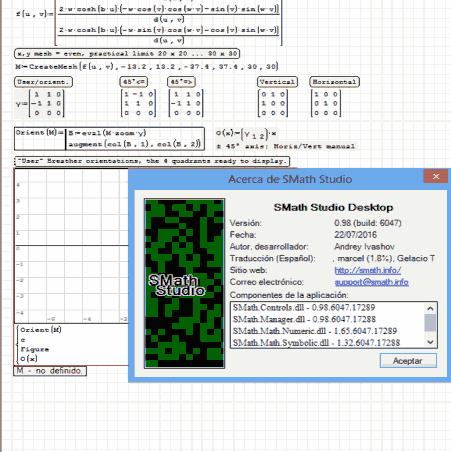
Method A.B. Draghilev and animation spatial mechanisms - Ber7 - Messages

3d.sm (446.66 KiB) downloaded 1164 time(s).
It would be better to put the animation in a 3/4 view . Would that be possible?
Best Regard
Carlos
WroteHello Jean ,
It would be better to put the animation in a 3/4 view . Would that be possible?
Best Regard
Carlos
Hello Carlos,
"3/4 view" : like setting TV screen 3/4 or other style.
You could scale the vertical vector, it would end being
hugly. The x, y ranges in the CreateMesh have these limits
under the hood. These limits are what make the Breather
so pleasant like the Eiffel shape.
Attached the 4 fixed orientations.
Jean
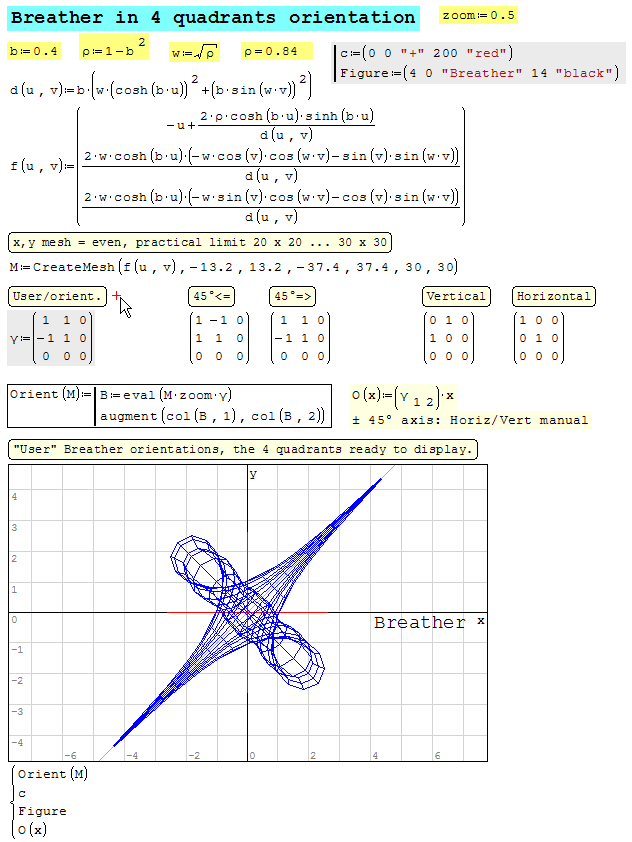
Rotate Breather [4 Orientations].sm (17.15 KiB) downloaded 993 time(s).
Axis joints intersect at the center of the sphere


3d1.smz (97.21 KiB) downloaded 1144 time(s).
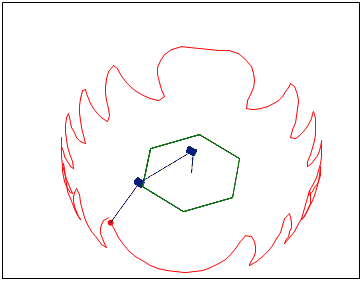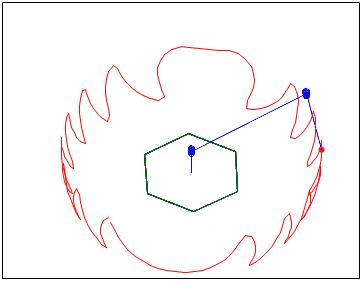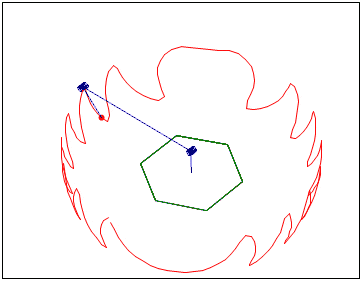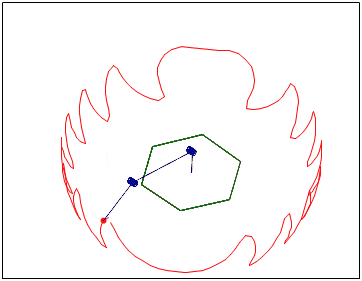
The working body of the manipulator moves along a given trajectory.
To solve the problem, 5 equations with six unknowns were used.
-Two link length equations
-Equations of the condition that the links are in the same plane
-Two space curve equations
Puma.sm (34.85 KiB) downloaded 1136 time(s).
https://espace.curtin.edu.au/bitstream/20.500.11937/7649/2/203604_136865_Schatz_JMES_author_draft_02.pdf
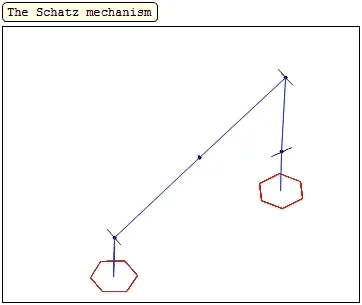
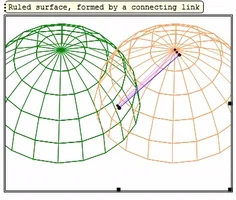
The Schatz mechanism provides a perfect dynamic balance
оf both centripetal and centrifugal forces as patented in 1971
as the only widely-used overconstrained linkages in industry,
mainly used as spatial mixing-machines.
Shatz 2cikla.sm (128.56 KiB) downloaded 1131 time(s).
WrotePuma manipulator
The working body of the manipulator moves along a given trajectory.
To solve the problem, 5 equations with six unknowns were used.
-Two link length equations
-Equations of the condition that the links are in the same plane
-Two space curve equations
In my option this system have
- Rigid link between 2 points
- 2 equations about belonging 2 points to the same sphere
- x2*y1-y2*x1
- some sin curve
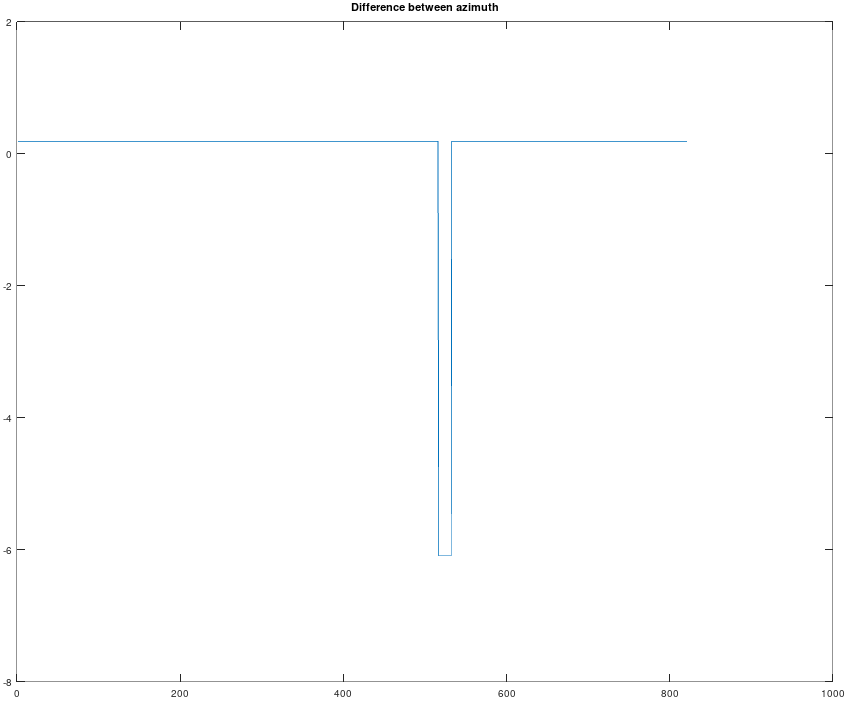
Don't quite understand about x2*y1-y2*x1. Some spherical meaning? The difference between azimuth angles is not perfect equal. Replace with atan(y1/x1)-atan(y2/x2) to make perfect equal.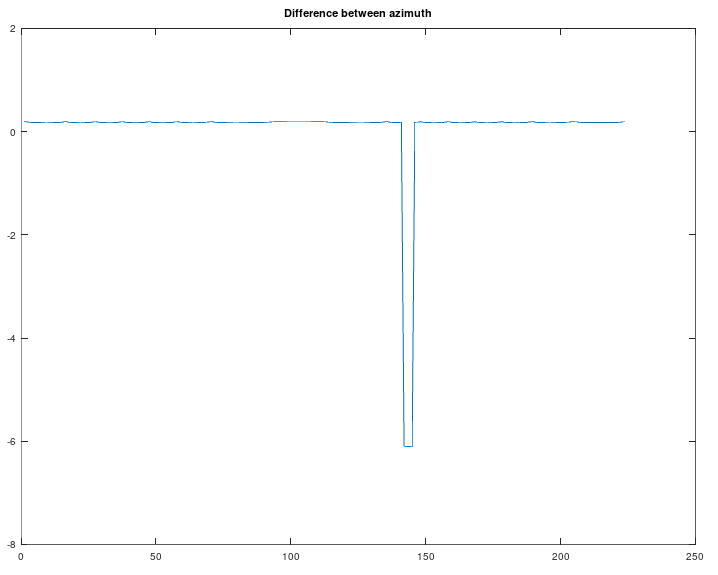
Wrote
In my option this system have
Hi grelkin2. Please provide your equations so that the solutions can be compared.
Best regards
WroteThe Schatz mechanism
The Schatz mechanism provides a perfect dynamic balance
оf both centripetal and centrifugal forces as patented in 1971
as the only widely-used overconstrained linkages in industry,
mainly used as spatial mixing-machines.
It has equation four points are coplanar
Maxima gives me this equation is exactly is zero with any coordinate
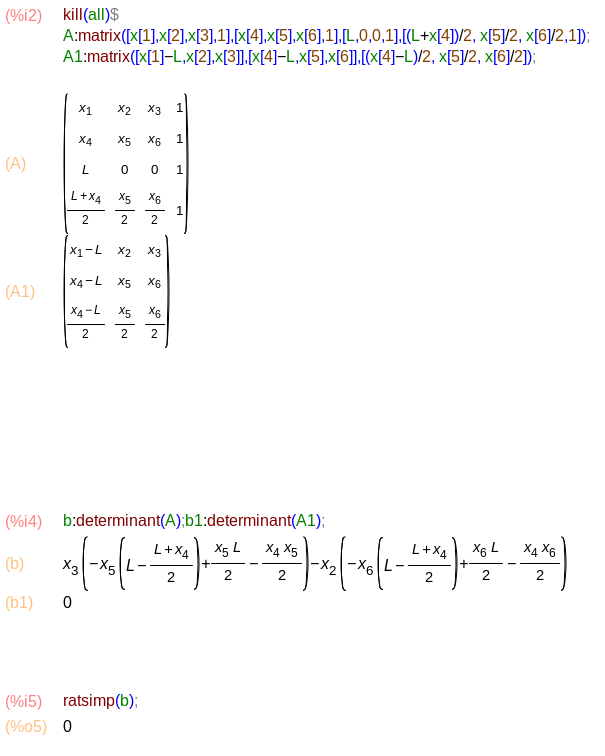
of the middle link are constantly perpendicular to each other.
In this case, one vertical rack (input link) rotates uniformly.
This is for those who are interested.
And Draghilev's method does not directly work in this case.


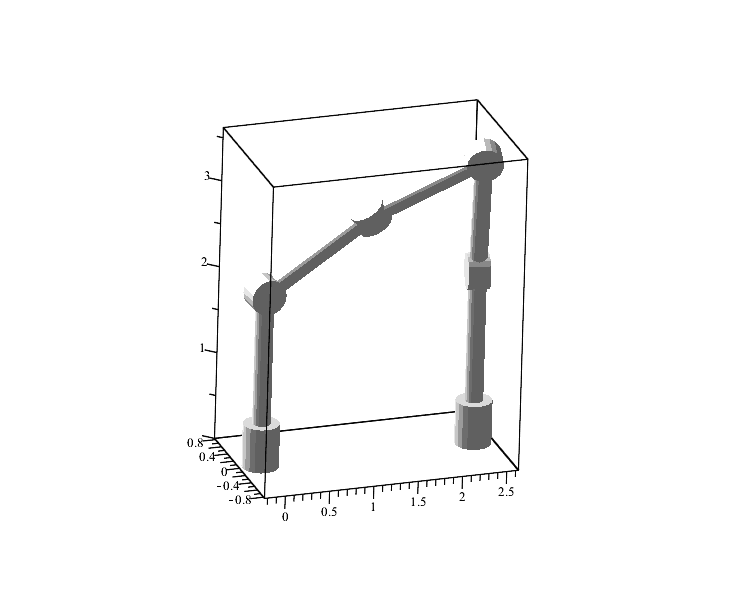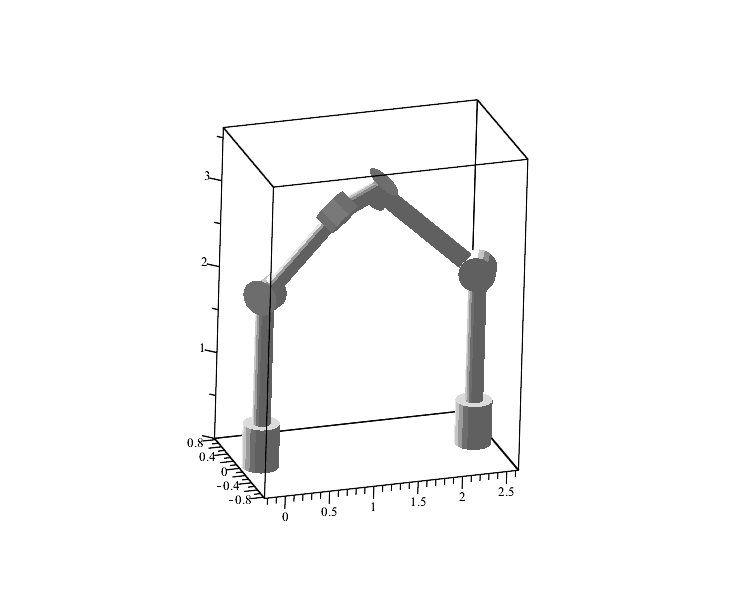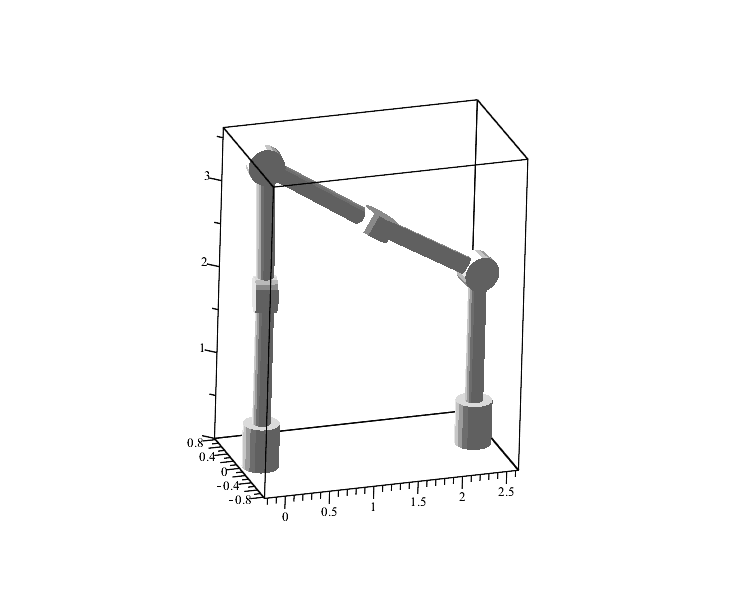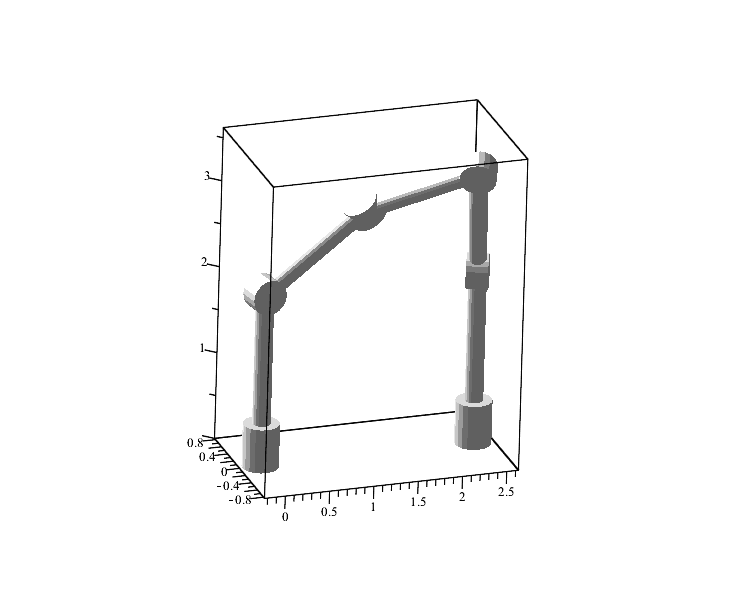
You can also check the perpendicularity of the hinges
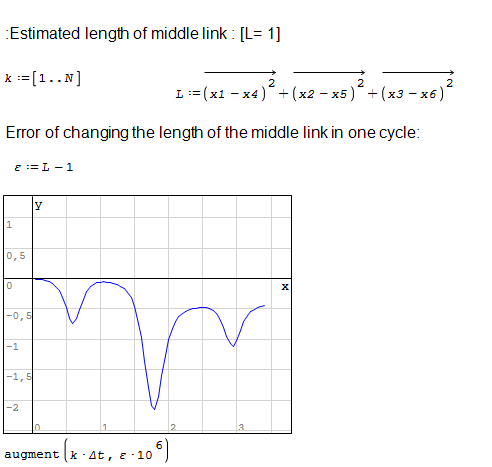
Proverka.sm (47.9 KiB) downloaded 1110 time(s).
Not really understand Schatz system
Please correct me if I'm wrong
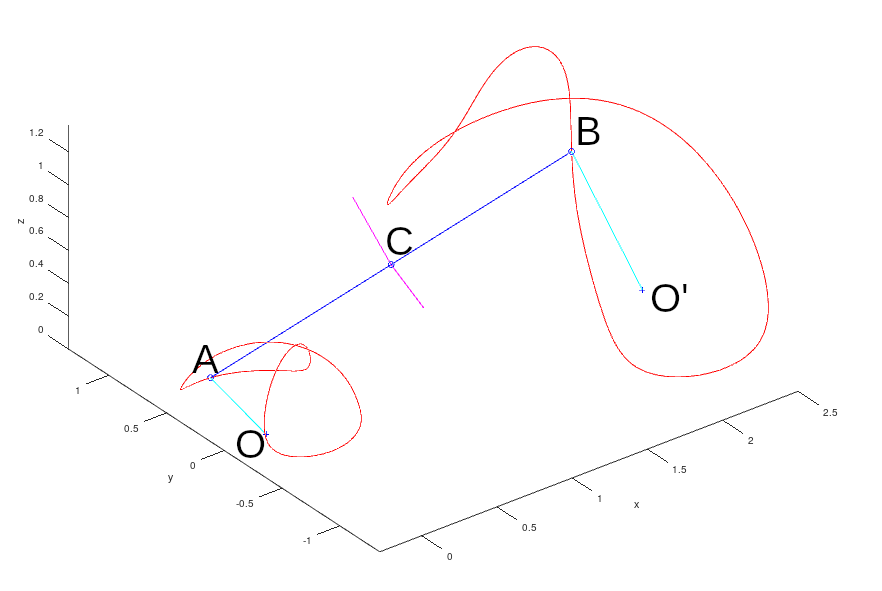
AO=const, BO'=const, AB=const
С extra point, AC=CB
Still two equation, one as I understand Z1*Z2=const?
and the last one is
Normals to planes ABO and ABO' must be perpendicular?
Magenta lines are normal vectors to ABO and ABO'
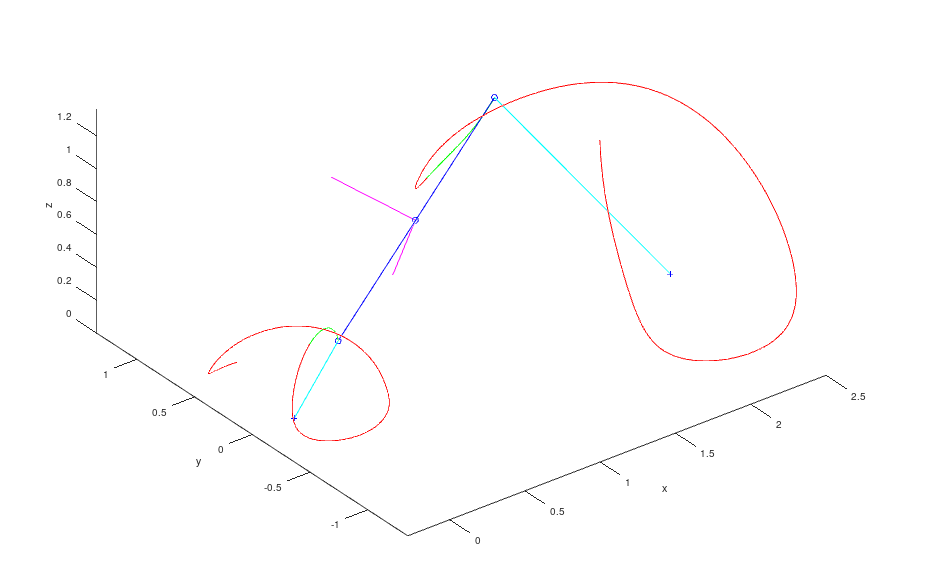
Pause and check perpendicularity
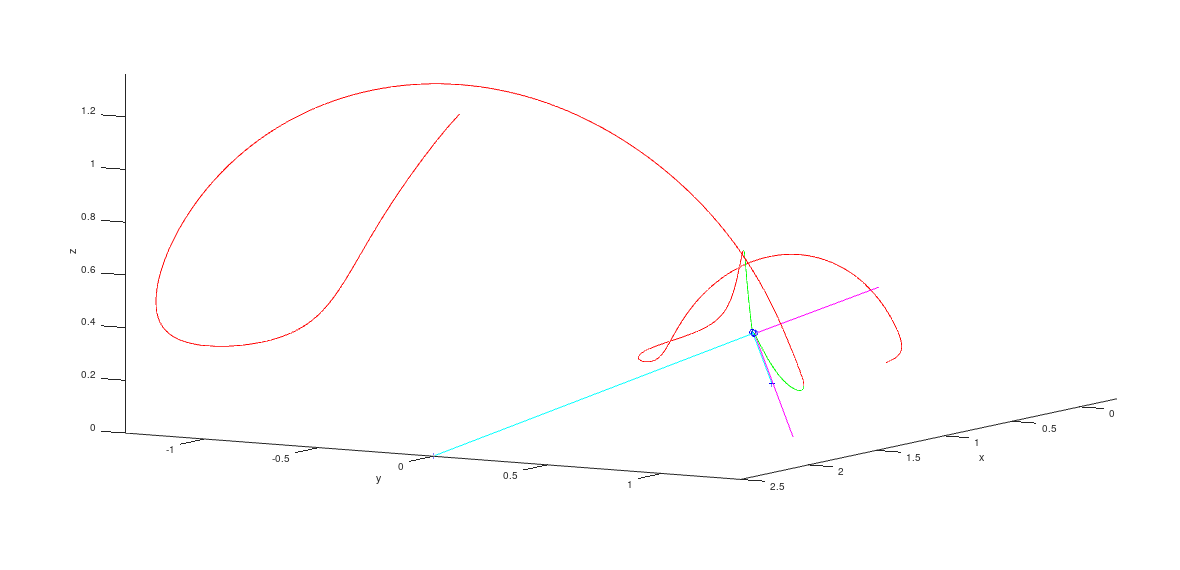
Rotate the view to get best observation
Make animation in mov format for the best quality, If not working, message me
Animation schatz.mov (285.1 KiB) downloaded 244 time(s).
"Normals to planes ABO and ABO' must be perpendicular?" Yes.
Regards
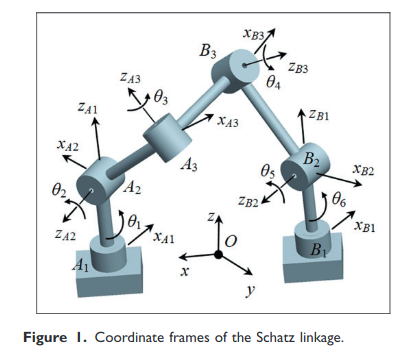
sinθ_2*sinθ_5=const
θ_2, θ_5 rotating angles around the ZA2, ZB2 rotating axis, difficult equation
You cann't use any intial values for coordinates because ABO and ABO' must be perpendicular, if you fixed all coordinates but one, you've got Quadratic equation. If you have no real roots change others coordinates and try again. Also you can change equation to be cos(α)=const, α≠90, α is angle between normals
WrotePlease correct me if I'm wrong
Не видел здесь твоих сообщений, потому что давно сюда не заглядывал. Если ещё интересуешься этим механизмов, то здесь находятся тексты на Maple с вариантом его реализации. И там же происходит общение, похоже, со специалистом.
Wrote
Не видел здесь твоих сообщений, потому что давно сюда не заглядывал. Если ещё интересуешься этим механизмов, то здесь находятся тексты на Maple с вариантом его реализации. И там же происходит общение, похоже, со специалистом.
Я могу вспомнить систему и туда выложить. Но не будут ли завсегдатаи против, если я не буду использовать Maple, а буду выкладывать картинки, видео, формулы?
WroteÐо не бÑдÑÑ Ð»Ð¸ завÑегдаÑаи пÑоÑив, еÑли Ñ Ð½Ðµ бÑÐ´Ñ Ð¸ÑполÑзоваÑÑ Maple, а бÑÐ´Ñ Ð²ÑкладÑваÑÑ ÐºÐ°ÑÑинки, видео, ÑоÑмÑлÑ?
Там это не здесь. Единственное, думаю, если в понятной для всех людей форме и в доступном для буферизации виде. Потом, одна стойка должна быть входным звеном, и чтобы это было чётко видно на анимации. Другими словами, чтобы было не хуже чем там и чтобы любой пользователь Maple мог легко проверить результат. Все тамошние пользователи, у которых значок модератора, могут сделать замечание или просто удалить сообщение. Например, там автоматически ни у кого нет права писать в раздел, предназначенный для сотрудников MapleSoft, которые помечены своим значком.
Хотя текст сообщения, насколько помню, разрешается набирать на любом языке, лишь бы с ним справлялся переводчик. А в плане обучения Maple считаю тот форум очень хорошим, если что.
- New Posts
- No New Posts