See please
[url=https://en.wikipedia.org/wiki/Track_transition_curve]

Wrote

See please
[url=https://en.wikipedia.org/wiki/Track_transition_curve]

We can animate Fresnel ... possibly a decreasing circle.
Can we superpose both on same animation ?
Jean

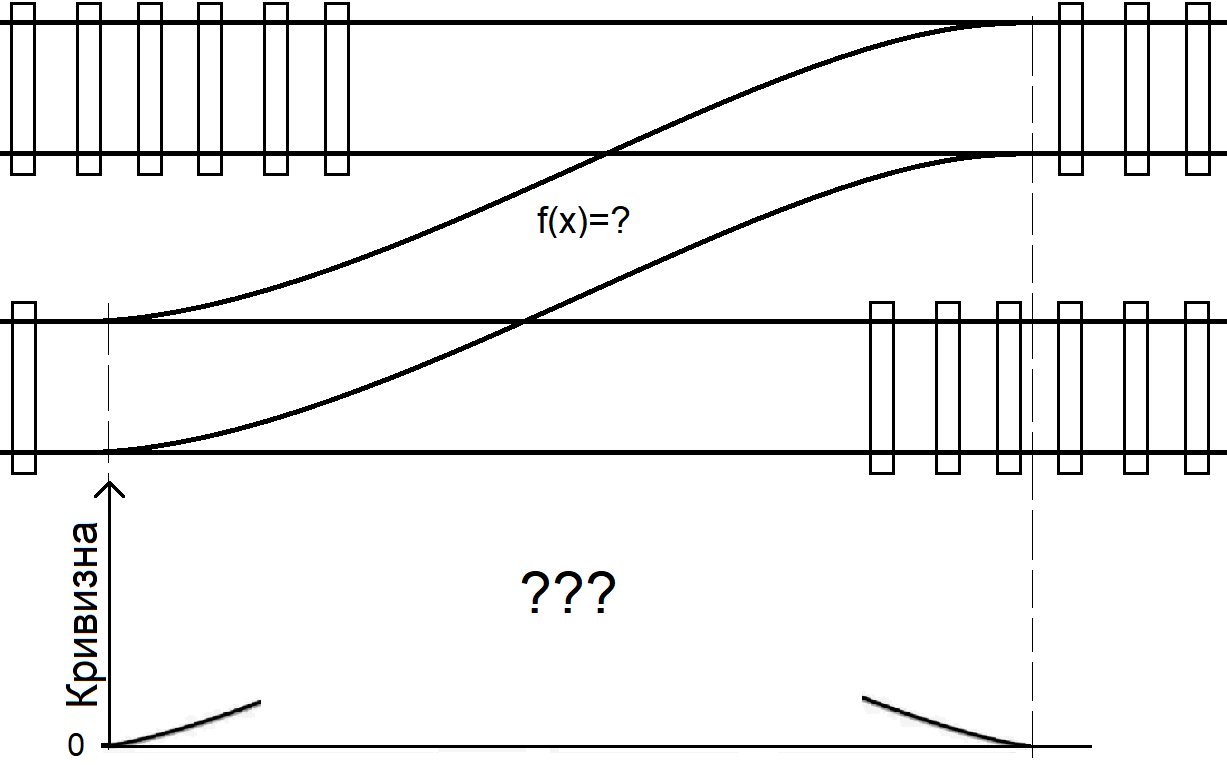
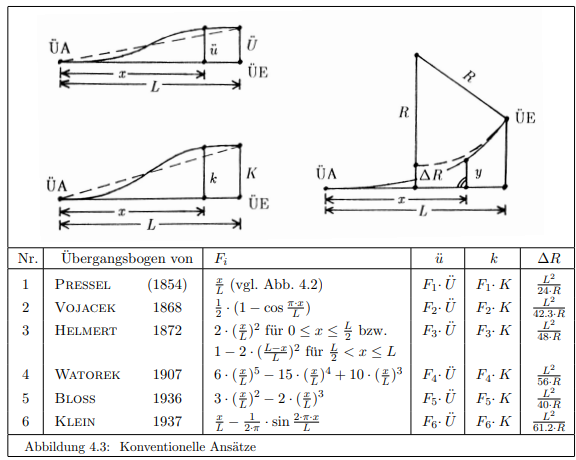
For the connection of two parallel tracks (crossover) you need two turnouts with (signed) curvature changing from zero to maximum back to zero to negative maximum and again back to zero. In the paper cited below various types of transition curves are given. The mmost popular one is the clothoide with a linear change of curvature with arc length (case 1 in the table). It produces much better transitions than just connecting straight segments and circular arcs (which for moderate speeds up to 50 km/h still is state of the art). More sophisticated transition arcs have been proposed because usually there is a superelevation (Überhöhung, возвышение) of the track to compensate for lateral acceleration.

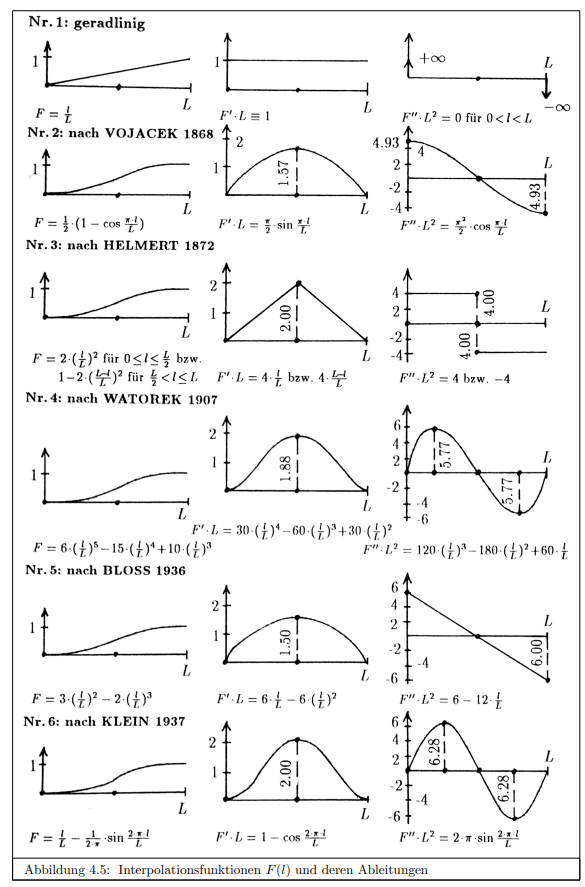
In the tables below F is the interpolating function for the curvature and the superelevation (they are proportional for a given speed). Some of them have second order smoothness of curvature.

To get f(x) you need to integrate F(x) twice. For slender transitions the difference between x and arc length can be neglected. In case 1 this gives a cubic parabola instead of a clothoide.

Note that a crossover requires four such segments as explained above.

Schuhr, P. (2007) Übergangsbogen für Bahnen mit hohen Fahrgeschwindigkeiten. In: Angewandte Geodäsie. Verlag der Bayerischen Akademie der Wissenschaften

[url=https://community.ptc.com/t5/Mathcad/Curve-for-switch-transition/m-p/913097]