I've tested Akkerman Function calculation in many programming environments. The best result I got is Akkerman (3, 14) = 131069 (Lazarus/FreePascal)
The worst one is been gotten in SMath Studio. It is Akkerman (3, 4) = 125. If I try to get Akkerman (3, 5) in SMath Studio it hangs out and crashes.
Even MathCAD gives better result And MathCAD is does not crash...
Akkerman.sm (4 KiB) downloaded 49 time(s).

See SS-2294.

Wrote

Even MathCAD gives better result

.

Sure Mathcad gives better result, because of its 64 floating point
accessibility to the machine resources. Smath is only 32 bits floating
point. I have pointed that several times and proved it. I was replied
Smath was also 64 bit ... proof in hand it is not !

That said otherwise, granularity of both: the machine and the engine.
In this context the first granularity is from "Smath engine'.

When I talk about Smath: I talk about the "stable" 5346.
What's new is new so often.

"The Ackermann function is the simplest example of a well-defined total function which is computable but not primitive recursive, providing a counterexample to the belief in the early 1900s that every computable function was also primitive recursive (Dötzel 1991). It grows faster than an exponential function, or even a multiple exponential function.

Visit the links: (OEIS A014221), (OEIS A001695).

Ackermann Number, Computable Function, Goodstein Sequence, Power Tower, Primitive Recursive Function, TAK Function, Total Function, quote from Wolfram".

... this result is too long to be displayed in one page,
Smath does not accomodate the copy to clipboard. Only
portion is viewed. I have nothing to tell me if the long
fraction is equivalent to 64 bit.

Wrote

Sure Mathcad gives better result, because of its 64 floating point
accessibility to the machine resources.

The Ackermann function causes 'stack overflow' error, not 'out of range' error.

Quote

The Ackermann function, due to its definition in terms of extremely deep recursion, can be used as a benchmark of a compiler's ability to optimize recursion.

Wrote

The Ackermann function causes 'stack overflow' error, not 'out of range' error.

Would you be kind enough to disambiguate [explicit] your distinction.
Whichever the distinction: isn't by lack of floating point capability?

Thanks, Jean

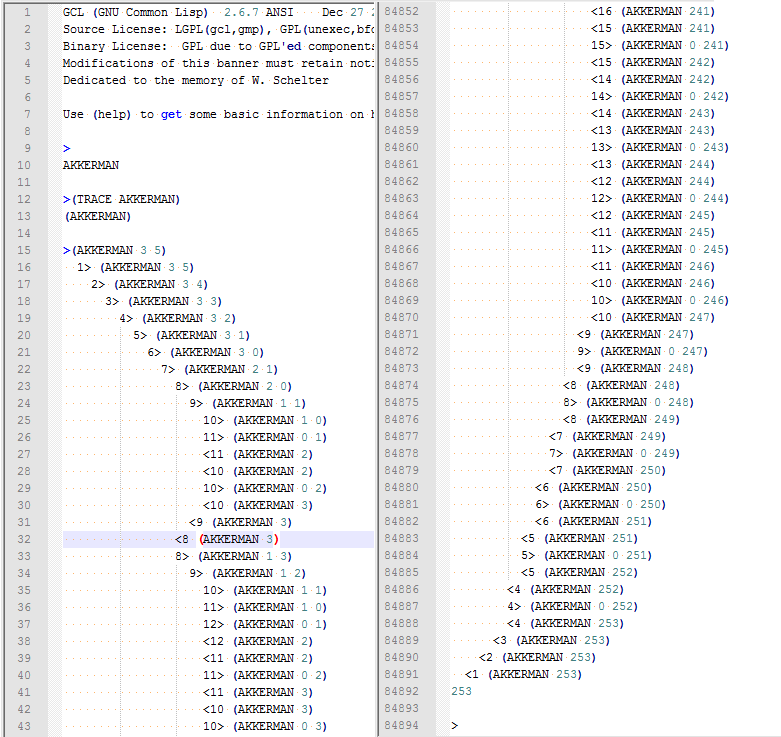
This is the beggining and the end of akkerman(3,5) tracing in GCL. As you can see, the numbers are not tremendous, but the number of numbers is tremendous.
For example, akkerman(3,4) requires 4 times less operations. As bigger stack as more conses you can add to it, no matter their values. if stack is too small it causes stack overflow.




And this is the death of akkerman(3, 6).




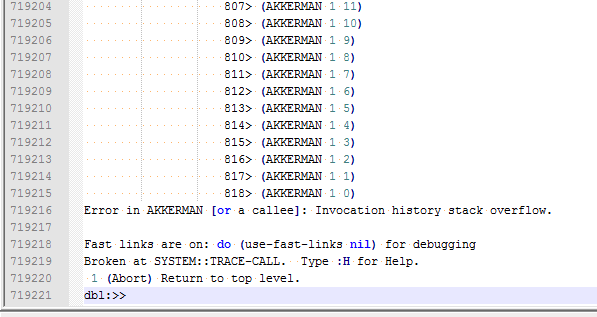
In opposite conner, the factorial function causes out of range error on 171 as argument, so stack is not overflown, but the product of n & fact(n-1) is out of range. And Smath is not crashes.

Here's a 2284-lines long call stack for SMath 0.98.5953 at the time of crash for Akkerman(3,5): Akkerman-3-5-crash.txt (322 KiB) downloaded 27 time(s).

@ur_naz

The problem here is at least two-fold.
1. The hard-crash (its BTS link was mentioned above).
This problem must be solved taking into account that SMath is .NET 2.0 application. As such, it cannot catch and recover from stack overflow exceptions; so the only way is to prevent them from happening.
Three ways here:
a. Use a counter to check call depth. It may be a program's internal counter, or .NET internal statictics available from StackTrace.FrameCount. Anyway, program has to use some empirical number, after which it should break execution and return an error. While this is the simplest approach, it cannot account for possible changes in stack size (e.g., different frameworks like Mono), and for differences in stack usage of different functions. It will either be too conservative, disallowing otherwise possible deep recursions, or somewhat risky, saving from most, but not all, SOEs.
b. Use RuntimeHelpers.EnsureSufficientExecutionStack Method. This may be preferrable, as it allows to check for really available stack space, thus making use of stack most efficiently. But it requires .NET 4+, thus may only be available if author decides to bump the project baseline (which may be undesirable on other reasons). Using unmanaged code here cannot help, because it runs in another thread with its own stack, and anyway, this wouldn't be portable. Using mixed .NET2/.NET4 DLLs isn't an option, too, because it requires that these DLLs run in their own frameworks, so different threads -> different stacks.
c. Use dedicated process for calculations. It's very costly, but could be an option if program intercepts too deep stack level, and restarts the calculation in a dedicated process only then. I doubt that this path will be taken.

Solving this part won't make SMath results better, but will prevent data loss and frustration.

2. A recursion optimization. Well, this is a task of its own. SMath only recently started to make first steps in optimizations, so for now, recursion lacks even simple tail optimization. Hopefully, someday SMath will be able to improve here to compete with other software in your list