I can plot an ellipse or a hyperbola
See please Ellipse-Hyperbola.sm (11 KiB) downloaded 33 time(s).
But cannot plot cubic lines.
Cubica.sm (29 KiB) downloaded 32 time(s).
Is it my or SMath error?
See please also
https://community.ptc.com/t5/Mathcad/Cubica/m-p/496877

Thanks!

Hi Vladimir. The problem is the poor quality of SMath's numerical code for linear algebra. A workaround is to redefine the determinant using some plugin.

Cubica.sm (31 KiB) downloaded 39 time(s).

Best regards.
Alvaro.

General case.

Homogeneous Curve.sm (27 KiB) downloaded 27 time(s).

Best regards.
Alvaro.

Спасибо!
Вот цитата из моей с А.И. Тихоновым книги
https://lanbook.com/catalog/informatika/math-cad-i-python-obuchenie-po-tekhnologii-stem
Инженер: ...вопрос к разработчикам, который не надо стесняться задавать либо им, либо на форумах, где общаются пользователи программ. Часто оказывается, что ответ на вопрос уже есть, его нужно только найти с помощью поисковой системы.
Студент: Где нужно это искать?
Математик: Практически для каждой математической системы имеется сообщество пользователей. Разработчики обычно поощряют эти сообщества, так они помогают поддерживать систему, устранять ошибки, формировать направления ее развития. Активными являются сообщества пользователей Mathcad и MATLAB. Несколько хуже обстоит дело с бесплатными системами. Сил и возможностей у их разработчиков существенно меньше.
Кстати, если у вас не хватает знаний, навыков или просто времени на решение задачи, то можно ее «повесить» на форуме и дождаться решения. Вот пример такой работы https://en.smath.com/forum/yaf_postsm82878_Cubic-lines.aspx
Thank you!
Here is a quote from my with Anton Tikhonov book
https://www.routledge.com/STEM-Problems-with-Mathcad-and-Python/Ochkov-Stevens-Tikhonov/p/book/9781032131658
Engineer: ...a question for developers that you shouldn’t be embarrassed to ask either them or on forums where users of the programs you work with communicate. It often turns out that the answer to a question already exists; you just need to find it using a search engine.
Student: Where should I look for this?
Mathematician: Almost every mathematical system has a community of users. Developers usually encourage these communities, so they help maintain the system, fix bugs, and shape the direction of its development. Mathcad and MATLAB user communities are active. The situation is somewhat worse with free systems. Their developers have significantly less strength and capabilities.
By the way, if you do not have enough knowledge, skills, or simply time to solve a problem, then you can “post” it on the forum and wait for a solution. Here is an example of such work https://en.smath.com/forum/yaf_postsm82878_Cubic-lines.aspx

Wrote

Hi Vladimir. The problem is the poor quality of SMath's numerical code for linear algebra. A workaround is to redefine the determinant using some plugin.

Best regards.
Alvaro.

Yes, Vladimir is a very famous name - Vladimir Lenin, Volodymyr Zelensky, Vladimir Putin...
But fortunately I am Valery ;-)

See please
https://oeis.org/search?q=2%2C+5%2C+9%2C+14%2C+20%2C+27%2C+35%2C+44%2C+54%2C+65%2C+77%2C+90%2C+104&language=russian&go=%D0%9F%D0%BE%D0%B8%D1%81%D0%BA

Limit at n=10

Wrote

... Yes, Vladimir is a very famous name - Vladimir Lenin, Volodymyr Zelensky, Vladimir Putin...
But fortunately I am Valery ;-)

Please, excuse me. I generally remember faces a little better, but I'm a disaster with names.

Wrote

By the way, if you do not have enough knowledge, skills, or simply time to solve a problem, then you can “post” it on the forum and wait for a solution. Here is an example of such work https://en.smath.com/forum/yaf_postsm82878_Cubic-lines.aspx

In maintenance we say: the important thing is not to know how to repair something, but to have the phone number of someone who knows.

Wrote

See please
https://oeis.org/search?q=2%2C+5%2C+9%2C+14%2C+20%2C+27%2C+35%2C+44%2C+54%2C+65%2C+77%2C+90%2C+104&language=russian&go=%D0%9F%D0%BE%D0%B8%D1%81%D0%BA

Yes, that's the sequence. It is the number of coefficients that have a homogenous bilinear form in two variables. And is the number of rows in the matrix 'v' in the file.

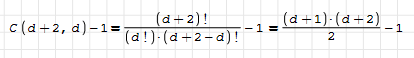
Wrote

Limit at n=10

I put the comments backwards. For big n, disable the SMath matrix inverse method and use dn_LinAlgSolve.



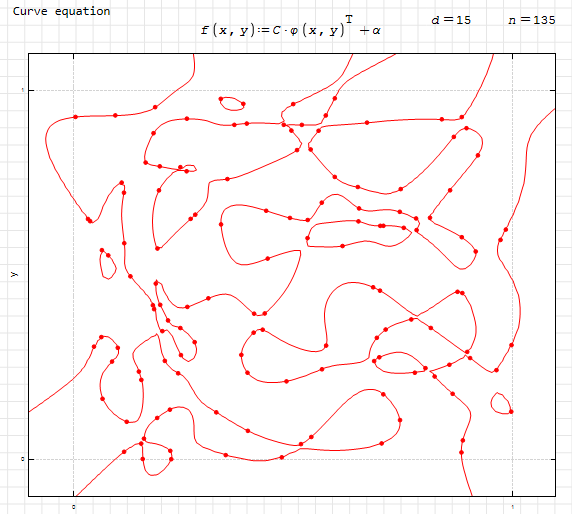
Homogeneous Curve.sm (31 KiB) downloaded 17 time(s).

I suppose it can be easily generalized to three dimensions, except for the part of graphing the surface, since there we would not have the usefulness of XYPlot to graph implicit functions.

Best regards.
Alvaro.

Wrote

I suppose it can be easily generalized to three dimensions, except for the part of graphing the surface, since there we would not have the usefulness of XYPlot to graph implicit functions.

With n level curves, one passes through each X,Y pair at level Z. For d=1, we have a plane, d=2 a quadric, etc.



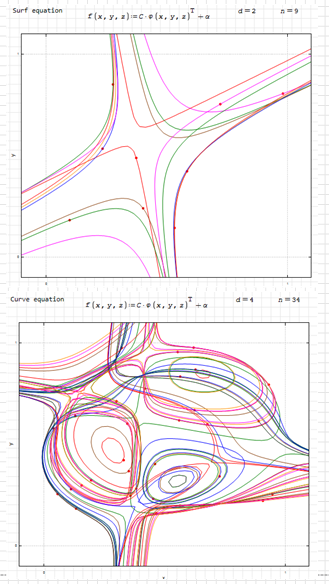
Homogeneous Surface.sm (33 KiB) downloaded 21 time(s).

Best regards.
Alvaro.