Hi. I have some issues in the attached.

Thanks in advance.

Alvaro.

cspline test.sm (37 KiB) downloaded 64 time(s).

Wrote

Hi. I have some issues in the attached.

Thanks in advance.

Alvaro.

Two red remain ... but here the XY plot.

Cheers, Jean



cspline test.sm (42 KiB) downloaded 49 time(s).

Hi Jean. Thanks, but you know me ... I want to use my own function.

Best regards.

Alvaro.

Two red will disappear if you use for loops instead of vectorization.

Regards,
Radovan

Wrote

Hi Jean. Thanks, but you know me ... I want to use my own function.

I messed your coding to make readable.
As it looks, you seem to implement Hermite cubic or an unknown brew ?
Hermite [the Draftsman spline] fits better in certain region,
but is discontinuous at junctions and as such has little interest.
In short, it can be used to create some additional best points
for the next more conventional l_p_c splines, for them now to
be continuous at points, thus analytical up to 2nd order derivative.
Hermite was exhausted in Mathcad, all converted Smath.
If of interest, will be please to attach.
Your original coding did calculate 'V' , but not the freaked code.
Some sort of "shadow in context".

Jean

cspline test[NFG].sm (53 KiB) downloaded 41 time(s).
Spline l_p_c [dspline, fintegrate].sm (78 KiB) downloaded 39 time(s).
Spline l_p_c [Recovered].sm (129 KiB) downloaded 39 time(s).

Hi Jean. There are not to much shadow in that small code. It's just the implementation of the traditional spline interpolation. In SMath there are not, or I can't found, the function cspline. The interpolation with cinterp in SMath evaluates the vector V each time that you call it, it's always better to have V=cspline(X,Y) and then call interp(V,X,Y,x). Finally, I want to implement an adaptive step size for the intervals in X. But first I see very convenient to have vectorization and plotting issues solved.

CS only do what mathcad's cspline do:



Best regards.
Alvaro.

Wrote

Hi Jean. There are not to much shadow in that small code. It's just the implementation of the traditional spline interpolation. In SMath there are not, or I can't found, the function cspline. The interpolation with cinterp in SMath evaluates the vector V each time that you call it, it's always better to have V=cspline(X,Y) and then call interp(V,X,Y,x). Finally, I want to implement an adaptive step size for the intervals in X. But first I see very convenient to have vectorization and plotting issues solved.

CS only does what Mathcad's cspline does:

The interpolation with cinterp in SMath evaluates the vector V each time that you call it, it's always better to have V=cspline(X,Y) and then call interp(V,X,Y,x)


1. You have a good point, but invalid: cinterp(X,Y,x) works faster than Mathcad [I tested long time ago].
2. Not supporting vectorization has only one answer to me:
all that stuff is scalar wrt 'x' for the canvas plot only,
but it is NOT a real scalar function like the built-in ones ... sin(x), cos(x), exp(x) ...
3. For the adaptive step size, you may have to invent the wheel or implement
Robert A. [Lagrange quadratic knots ... stricking example attached].

Resume:
1. cinterp => hyperfast
2. Vectorization ... left unsolved
3. adaptive step size => suggested

Thanks Alvaro, most interesting ... Jean

cspline test (1).sm (62 KiB) downloaded 47 time(s).
Spline Lagrange [Quadratic knots EXPERIMENTAL].sm (47 KiB) downloaded 41 time(s).

CSplines with adaptive steps. Same issues, but now can use zero with units, at least in the adaptive case.

Best regards.
Alvaro.

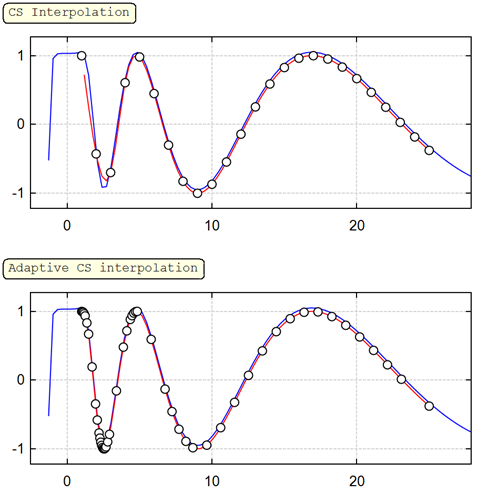
adapt cspline test.sm (83 KiB) downloaded 53 time(s).

Wrote

...
Resume:
1. cinterp => hyperfast
2. Vectorization ... left unsolved
3. adaptive step size => suggested
...

I will add this as well, if you do not mind.

Two of the main reasons we want to use interpolation (cinterp f.e.).
I think I mentioned this many times...
...
4. numerical derivation ... left unsolved
5. numerical integration => solved?
....

Regards,
Radovan

Wrote

I will add this as well, if you do not mind.

Two of the main reasons we want to use interpolation (cinterp f.e.).
I think I mentioned this many times...
...
4. numerical derivation ... left unsolved
5. numerical integration =

Numerical derivation from the Smath d/dx is not possible ... WHY ?

The derivative operator derives wrt to rules that apply to function(s)
cinterp(X,Y,x) is not a function, only an interpolating function.
Alternately two ways:
1. from the dspline(s,X,Y,t) ... 's' from solving
2. from the infinitesimal D1(x,h,f) ... where 'f' is cinterp(X,Y,x)

Exemplified in the attached ... Jean

Page0 Cubic Copy.sm (104 KiB) downloaded 36 time(s).

Derivative and integral for regular cubic splines.
Best regards.
Alvaro.

di cspline test.sm (86 KiB) downloaded 70 time(s).

Wrote

Derivative and integral for regular cubic splines.
Best regards.
Alvaro.

1. Integrator does not recognize p(x)
2. D2(,x) works great.

Cheers ... Jean

di cspline test Otherwise.sm (51 KiB) downloaded 47 time(s).
di cspline test.sm (101 KiB) downloaded 35 time(s).

Wrote

Derivative and integral for regular cubic splines.
Best regards.
Alvaro.

1. I don't think you have any kind of spline for real application [added example].
2. From what I tested before Smath cinterp is universal [Matlab, Mathematica, Mathcad ...]
3. Read carefully: Smath ainterp [Akima] is unique to me to Smath.
From previous ad nauseum testing, it fits exceptionally well certain types of data
and is pure crap for other types of data, that's what it is. Superb for the example.
4. On the other hand, integrator supports cinterp, your coding does not.
The cumulative integration does between limits as well, just more greedy in time.
5. I don't understand all that crappy coding from download ... damned mystic !

All in all: most interesting. Thanks Alvaro.

di cspline test [SHORT] Copy.sm (104 KiB) downloaded 50 time(s).

Updated (Now it works again). Revised because the new develop of interpolation funcitons by Viacheslav at https://en.smath.com/forum/yaf_postsm75020_ODE-Solvers.aspx#post75020

This worksheet is about adaptive csplines and differentiation and integration of the splines.

cspline.sm (106 KiB) downloaded 61 time(s).

cspline.pdf (297 KiB) downloaded 41 time(s).



Best regards.
Alvaro.