subjected Equation is detailed as under:
In a Circle if S is arc length, L is chord length and R is Radius and 'Theta' is angle of arc subtented at centre of circle in radians.

then by geometry S = 'R'.'Theta', where Theta in radians and R is Radius.
or Theta/2 = S/2R -----Eq 1

and also in triangle made by R , L/2 and base from centre to one end of L/2
Sin (Theta/2) = L/2R ----Eq 2

thus from Eq 1 and 2
Sin (S/2R) = L/2R

if an Arc length 'S' is given = 2618.
its chord length 'L' is also given = 2280.
then equation will be Sin (1309X) = 1140X, Where X =1/R

The result iz zero (see the example of finding roots).
Try, for instance, function solve and solve the equation sin(1.309*x)-1.140*x (there should be three values)

By the way, if we try to plot the function sin(1309*x)-1140*x and zoom in, we are going to see very small numbers with the 15 significant digits on the axis ticks, say x.xxxxxxxxxxxxxxE-xx. This is rather hard to read especially on the x axis. I suppose that there should be used the same number of decimal places as defined under Tools=>Options=>Decimal places, or something else?

Regards,
Radovan

Wrote

The result iz zero (see the example of finding roots).
Try, for instance, function solve and solve the equation sin(1.309*x)-1.140*x (there should be three values)

By the way, if we try to plot the function sin(1309*x)-1140*x and zoom in, we are going to see very small numbers with the 15 significant digits on the axis ticks, say x.xxxxxxxxxxxxxxE-xx. This is rather hard to read especially on the x axis. I suppose that there should be used the same number of decimal places as defined under Tools=>Options=>Decimal places, or something else?

Regards,
Radovan

Dear Frnds
Actually in excel, values can easily be brought out by using Goal seek option. I am pasting here the same:

Radius Excel Formula and value

C9 - value = cos(1309/C9)-((C9-525)/C9)
1534.578119 -0.000162479

Here I put a additional formula:
sin(1309/R) - L/2R =0.

Radius C7 value Excel Formulae and value
=SIN(1309/C7)-(1140/C7)
1455.558167 -0.000306041

Next: Solution of sin(X ) or cos(X ) or other trigonometric functions could only be solved in form of expansion of series. So in place of sinaX or cosaX , that series can be replaced up to the required terms wrt the required decimal. But again it is a tedious due to multi power series
Sin(X) = X – (X^3)/3! + (X^5)/5! – (X^7)/7! + ---- -------- -------
Cos (X) = 1 – (X^2)/2! + (X^4)/4! – (X^6)/6! + ----- ----- ----

My TI 89 Titanium says 0 :P

If anyone cares...

We have a maths problem, not an Smath problem. 0 is a correct answer. AFAIK there is no other.

I solve using OpenOffice Spreadsheet (Goal Seek)and I get R = 1457.555. Zero is not the only answer, I believe.

Here it is, again

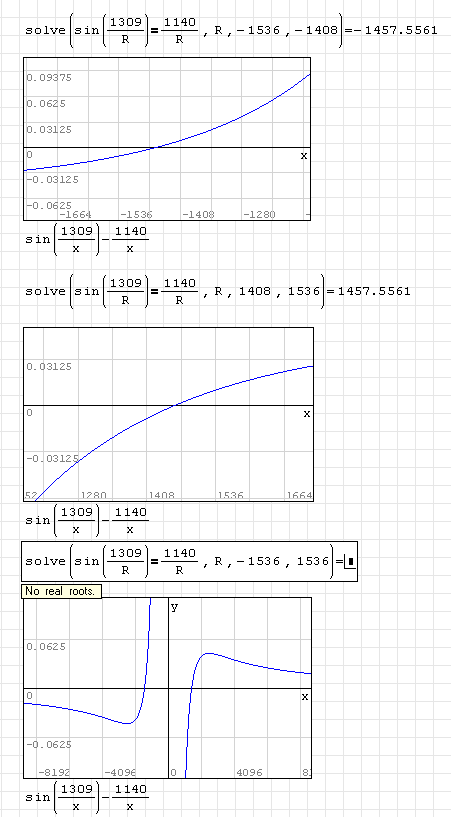
Regards,
Radovan