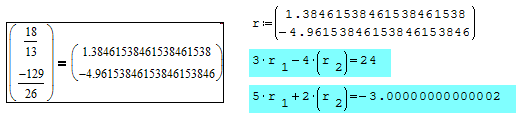1 страниц (13 вхождений)
2 equations with 2 unknowns - How to solve 2 equations with 2 unknowns - Сообщения
That is a good way! But I know that many high-school student don't really know linear algebra and that is why i asked 
But thanks for the fast answer!
// Wuxen
But thanks for the fast answer!
// Wuxen
Present it otherwise as you wish.
In the attached, in "So much from so little"
experiment 7.2 and 7.201 vs result !!!
Solve [x,y,z] Compactum.sm (62,73 КиБ) скачан 677 раз(а).
In the attached, in "So much from so little"
experiment 7.2 and 7.201 vs result !!!
Solve [x,y,z] Compactum.sm (62,73 КиБ) скачан 677 раз(а).
I understand what you are saying, but the thing I am looking for is:
In Matlab I can also solve 2 eqs. with 2 unknowns without using linear alg.
in Matlab I can solve it with solve(3*a-4*b=24 AND 5*a+2*b=-3,[a b])
I hope you understand what I'm looking for - It is to solve it without using linear alg.
// Wuxen
In Matlab I can also solve 2 eqs. with 2 unknowns without using linear alg.
in Matlab I can solve it with solve(3*a-4*b=24 AND 5*a+2*b=-3,[a b])
I hope you understand what I'm looking for - It is to solve it without using linear alg.
// Wuxen
You can use the built-in function roots()
![2016-06-29 09_27_49-SMath Studio Desktop - [roots.sm_].png](/ru-RU/files/Download/FpozMd/2016-06-29-09_27_49-SMath-Studio-Desktop---[roots.sm_].png)
Settings about roots' range are in Tools > Options > Calculation > Roots (range); you can also give an initial guess as third argument.
![2016-06-29 09_27_49-SMath Studio Desktop - [roots.sm_].png](/ru-RU/files/Download/FpozMd/2016-06-29-09_27_49-SMath-Studio-Desktop---[roots.sm_].png)
Settings about roots' range are in Tools > Options > Calculation > Roots (range); you can also give an initial guess as third argument.
If you like my plugins please consider to support the program buying a license; for personal contributions to me: paypal.me/dcprojects
WroteI understand what you are saying, but the thing I am looking for is:
In Matlab I can also solve 2 eqs. with 2 unknowns without using linear alg.
in Matlab I can solve it with solve(3*a-4*b=24 AND 5*a 2*b=-3,[a b])
I hope you understand what I'm looking for - It is to solve it without using linear alg.
There are many ways to solve, about ½ dozen more. Where do you see "linear alg"
in my reply ? My typical answer is over 3 centuries old, coded universal in any
system handling maths. Mathcad, Matlab ... they just code the solving like Smath
coding 2*3 =6. If you would have a system 1000 variables/unknowns, you would use
"linsolve", doing the same but more efficiently for speed of computation.
Gauss elimination, Cramer are not efficient. Above a certain size, Cramer will
never end between all big blues of the world together, and you will be dead
sucking roots for centuries.
2 пользователям понравился этот пост
2 пользователям понравился этот пост
Hi. To handle this needs a complete set of instructions, and a new system variable:
$MaxExtraPrecision is used implicitly in various exact numerical computations, including equality tests, comparisons, and functions such as Round and Sign.
See Possible issues under https://reference.wolfram.com/language/ref/Equal.html
Best regards.
Alvaro.
$MaxExtraPrecision is used implicitly in various exact numerical computations, including equality tests, comparisons, and functions such as Round and Sign.
See Possible issues under https://reference.wolfram.com/language/ref/Equal.html
Best regards.
Alvaro.
WroteWrote
Hi Davide,
unfortunately, your sanity check isn't good, because the result f(a,b )=[0;0] says the opposite: it's the result of logical expressions "is 3*a-4*b equal to 24? No (0)!" and "is 5*a+2*b equal to -3? No (0)!"
The error is small though, less that 4*10^-14.
Busted! Thank you Mike
(screenshot fixed)
![2016-06-29 09_27_49-SMath Studio Desktop - [roots.sm_].png](/ru-RU/files/Download/FpozMd/2016-06-29-09_27_49-SMath-Studio-Desktop---[roots.sm_].png)
If you like my plugins please consider to support the program buying a license; for personal contributions to me: paypal.me/dcprojects
NO Davide: not so much "busted". Even -3.00000000000004 is caused by
the machine ULP in the sanity reverse computation. Nothng to worry about.
Jean

Solve SANITY.sm (11,77 КиБ) скачан 765 раз(а).
the machine ULP in the sanity reverse computation. Nothng to worry about.
Jean

Solve SANITY.sm (11,77 КиБ) скачан 765 раз(а).
1 страниц (13 вхождений)
- Новые сообщения
- Нет новых сообщений

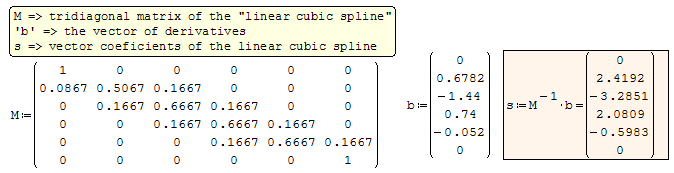
![2016-06-29 02_47_09-SMath Studio Desktop - [Page1_].png](/ru-RU/files/Download/zSsBYB/2016-06-29-02_47_09-SMath-Studio-Desktop---[Page1_].png)