Do you know what method uses the roots function?
Look at the areas of attraction to the roots. White color - no solution.

Wrote

Do you know what method uses the roots function ?

Smath roots plugin is essentially Newton.
Descartes used it about a century before.
roots(f(x),x,init)= very accurate

Wrote

Wrote

Do you know what method uses the roots function ?

Smath roots plugin is essentially Newton.
Descartes used it about a century before.
roots(f(x),x,init)= very accurate

I think the built-in roots function uses a different method than Newton. Which?

Wrote

I think the built-in roots function uses a different method than Newton. Which ?

I get same 15 decimals from either Newton/roots.
Occasionally, roots fails not being able to initialize.

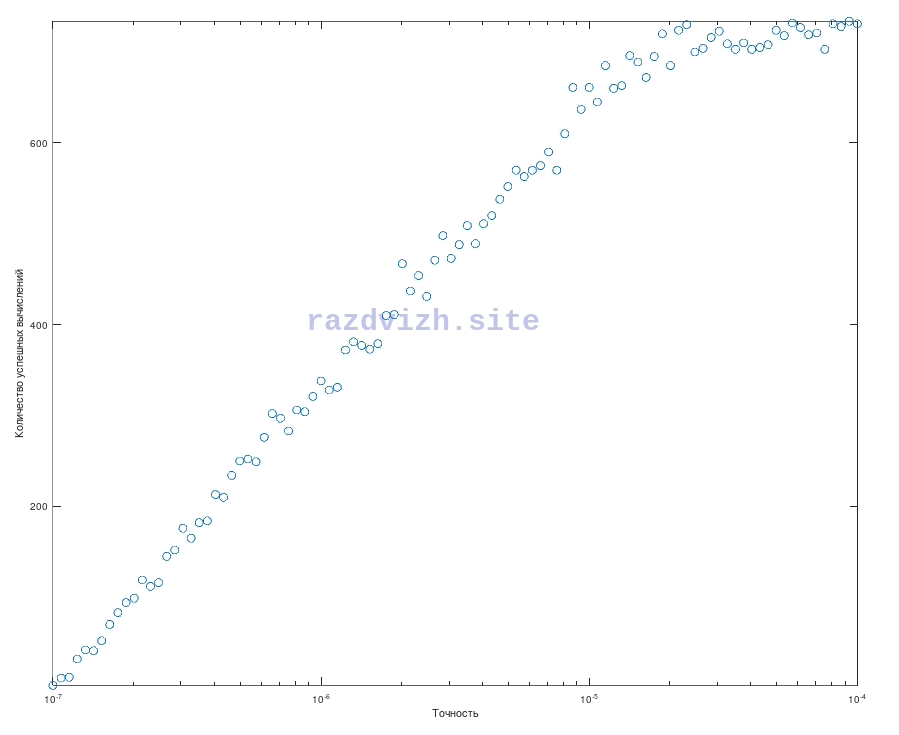
Рассмотрел данную систему в зависимости от задаваемой точности. Красным цветом обозначил точки, которые выходят в NaN, зеленным цветом точки, которые дают хоть одно решение. Часть решений показал желтыми линиями. При повышении точности "белые" области увеличиваются. Это те области, в которых при заданном числе шагов вычислений, не достигается никакого результата.
[ENG]
I considered this system depending on the specified accuracy. In red, I marked the points that go to NaN, in green, the points that give at least one solution. Some of the solutions were shown with yellow lines. As the accuracy increases, the "white" areas increase. These are the areas in which, with a given number of computational steps, no result is achieved.
[ENG]
Анимация polv1i.mov (1 МиБ) скачан 21 раз(а).

See please
One article about the Newton method

Wrote

See please
One article about the Newton method

Спасибо за статью.
Если мы говорим о алгебраическом многчлене f(z)=aₙ*zⁿ+..+a₁*z+a₀=0, aᵢ=const i=0..n
zᵢ=bᵢ+i*cᵢ - i-ый корень уравнения, (bᵢ, cᵢ) искомые вещественные и мнимые части i-корня.
При подстановке и последующей группировки решаем систему из 2-х уравнений Re(f(z))=0 и Im(f(z))=0

Я не вникал глубоко в решение систем с большим n. Мне кажется при нахождение корня с приемлемой точностью,
проверяется его кратность, является корнем его сопряжение, и затем исходный многочлен делится на решение,
степень опускается и снова ищутся корни многочлена меньшей степени.

Для уравнения z^3-5*z^2-1.5=0, после замены z=a+b*i
-3*a*b^2-5*(a^2-b^2)+a^3-1.5=0
-b^3+3*a^2*b-10*a*b=0
Я использую метод Драгилева для решения нелинейных уравнений. Добавлем новую переменную n и константы,
которые будут зависеть от начального положения, то есть уравнение будет
f1(z,n)=z^3-5*z^2-1.5+(a0+a1*i)*n=0, n=1, a0 и a1 такие что при z0=a0+b0*i f1(z0,1)=0
-3*a*b^2-5*(a^2-b^2)+a^3-1.5+a0*n=0
-b^3+3*a^2*b-10*a*b+a1*n=0

Что касается полюсов, областей устойчивости, все это сложная вещь, связанная с правой частью ду
Для уравнений (я ввел дополнительный параметр n)
(x^2+y^2)^2-2*(x^2-y^2)+a0*n-3=0
((x-.5)^2+(y-.5)^2)^2-8*((x-.5)^2-(y-.5)^2)+a1*n=0
Система ду будет следующая
dx/dt = ( -2.0e+1*a0*y+-4.0*a0*(x*x)*y+-4.0*a0*(y*y*y)+9.0e+0*a0+4.0*(x*x)*a1*y+6.0e+0*a0*(y*y)+4.0*a1*(y*y*y)+-2.0*a0*x+2.0e+0*a0*(x*x)+4.0*a1*y+4.0e+0*a0*x*y);
dy/dt = ( 2.0*a0*y+-4.0*(x*x*x)*a1+7.0e+0*a0+-2.0e+0*a0*(y*y)+4.0*x*a1+4.0*a0*x*(y*y)+-1.2e+1*a0*x+-6.0e+0*a0*(x*x)+-4.0*x*a1*(y*y)+4.0*a0*(x*x*x)+-4.0e+0*a0*x*y);
dn/dt = ( 4.0e+0*x*(y*y)+-2.0e+1*(y*y*y)+-8.0*(y*y)+9.6e+1*x*(y*y*y)+8.0e+0*((x*x)*(x*x))*y+-8.0e+0*(x*(x*x)*(x*x))+8.0*((x*x)*(x*x))+-3.2e+1*x*y+-8.0*(x*x)+3.6e+1*x+1.2e+1*(x*x)*y+-2.8e+1*(x*x*x)+-1.6e+1*(x*x*x)*(y*y)+1.6e+1*(x*x)*(y*y*y)+9.6e+1*(x*x*x)*y+-8.0e+0*x*((y*y)*(y*y))+-2.8e+1*y+8.0e+0*(y*(y*y)*(y*y))+-8.0*((y*y)*(y*y)));