Hi,

I do not understand from where it comes this error: Logarithm of zero is not defined.
Why in some cases maple/maxima can solve but Smath not, while in other not even maple/maxima cannot solve.

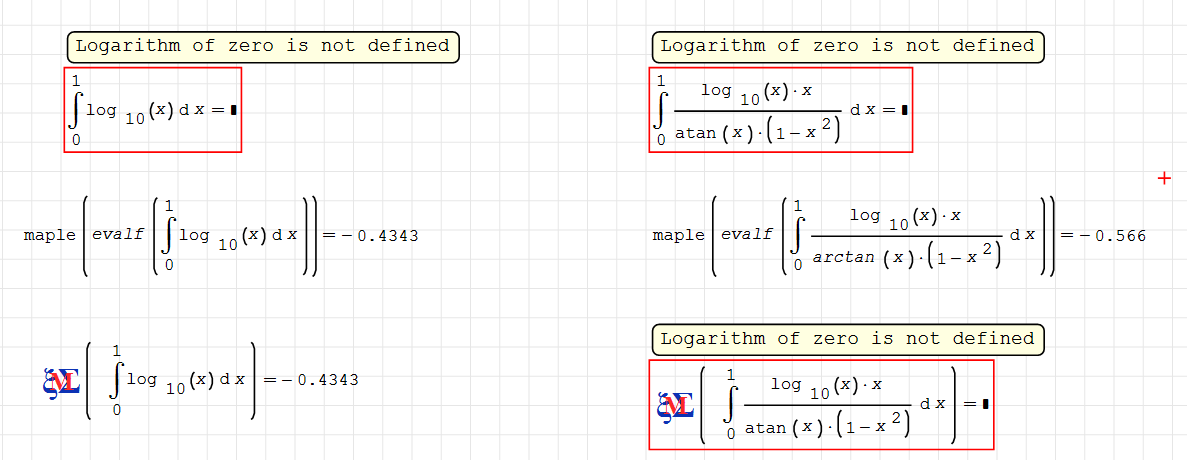
If you pay attention, the theorems about derivatives are about the open interval ( a , b ), while those about continuity and integration are about the closed ones [a,b]. However, there is a theorem, which I don't remember the name of or even if it has one, which states that given a definite integral you can exclude a finite number of points from the interval, which generalizes to an infinite but countable set. This is valid for the Riemann and Darboux integrals, and most likely for the Lebesgue and some others, but I don't remember that well. Applying that theorem, it can be stated that if Maple or Maxima find a primitive, they can apply the fundamental theorem of integral calculus to solve the integral, even if the integrand is not continuous at those points, because by that theorem you can discard them without altering the value of the integral. And since you are working on the closed interval, you can rule out the interval endpoints as well.

In the case of the first integral, both maxima and maple find a primitive, and get the same answer, but for the second case only maple does, and maxima, when trying to apply a numerical method, runs into the discontinuity, which you can avoid by integrating between 0+ε and 1-ε for "small" ε and see if a value is obtained, then studying the convergence of the applied numerical method and then estimating its error, or assuming that the method is robust enough to give a good value.

You can find this in any calculus book, in the chapter on improper integrals, and while it is fine to ask this, asking it in the questions subforum stating that SMath is unable to solve it, and not once, but about ten times, going around the same problem, does not seem like the best study strategy, neither for you nor for future visitors to the forum who will see the same question reported as a bug or lack of program development in the questions subforum, besides seeming like a very aggressive attitude on your part.

Best regards.
Alvaro.

Although Martin has already shown how to use maxima to estimate a numerically definite integral, its error and some other elements, so that what has been said is not just words, this is a procedure to use a well known Runge-Kutta-based ode solver to estimate a definite integral and thus be able to use the details of the procedure to study its convergence and limit its error, just because these details are very well explained in many books on numerical calculus. It also shows how to avoid indeterminacies in SMath.



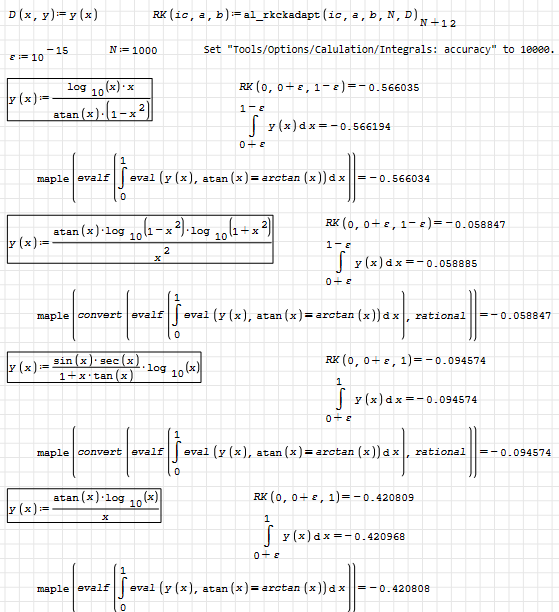
It can also be extended to double integrals, although SMath has a bug in them, since before it could calculate them normally.



improper-ints.sm (37 КиБ) скачан 28 раз(а).

improper-ints.pdf (214 КиБ) скачан 34 раз(а).


References

Maritn's post about Maxima quadrature:
- https://en.smath.com/forum/yaf_postst25506_Smath-cananot-solve-this-integral-No5-while-Mathcad-Prime-can.aspx

Single int: A bug in the odesolvers and its solution:
- https://en.smath.com/forum/yaf_postsm56081_Ode-solvers-implementation.aspx
- https://en.smath.com/forum/yaf_postsm57304_ODE-Solvers.aspx#post57304

Double int:
- https://en.smath.com/forum/yaf_postsm61577_Double-Integration-using-ode-solvers.aspx
- https://en.smath.com/forum/yaf_postsm85273_Mathcad-Toolbox.aspx#post85273

Maple convert/rational:
- https://en.smath.com/forum/yaf_postsm82867_Maple-Tools.aspx#post82867

Best regards.
Alvaro.