1 страниц (7 вхождений)
Intel ODE Solver Library - Intel ODE Solver Library - Сообщения
Intel ODE Solver Library






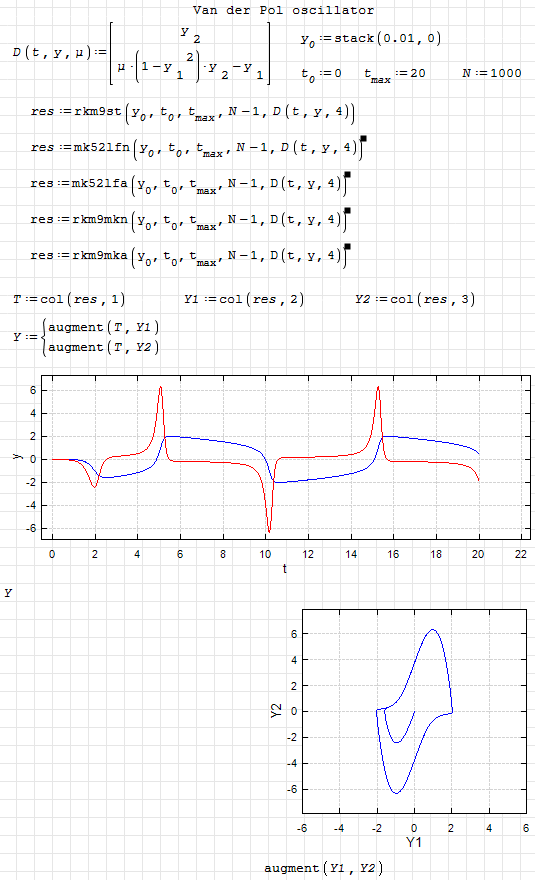
Functions list: rkm9st(5), mk52lfn(5), mk52lfa(5), rkm9mkn(5), rkm9mka(5).
rkm9st(init, x1, x2, intvls, D) A specialized routine for solving non-stiff and middle-stiff ODE systems using the explicit method, which is based on the 4th order Merson’s method and the 1st order multistage method of up to and including 9 stages with stability control.
mk52lfn(init, x1, x2, intvls, D) A specialized routine for solving stiff ODE systems using the implicit method based on L-stable (5,2)-method with the numerical Jacobi matrix, which is computed by the routine.
mk52lfa(init, x1, x2, intvls, D) A specialized routine for solving stiff ODE systems using the implicit method based on L-stable (5,2)-method with numerical or analytical computation of the Jacobi matrix. The user must provide a routine for this computation.
rkm9mkn(init, x1, x2, intvls, D) A specialized routine for solving ODE systems with a variable or a priori unknown stiffness; automatically chooses the explicit or implicit scheme in every step and computes the numerical Jacobi matrix when necessary.
rkm9mka(init, x1, x2, intvls, D) A specialized routine for solving ODE systems with a variable or a priori unknown stiffness; automatically chooses the explicit or implicit scheme in every step. The user must provide a routine for numerical or analytical computation of the Jacobi matrix.
Arguments:
- init is either a vector of n real initial values, where n is the number of unknowns (or a single scalar initial value, in the case of a single ODE).
- x1 and x2 are real, scalar endpoints of the interval over which the solution to the ODE(s) is evaluated. Initial values in init are the values of the ODE function(s) evaluated at x1.
- intvls is the integer number of discretization intervals used to interpolate the solution function. The number of solution points is the number of intervals + 1.
- D is a vector function of the form D(x,y) specifying the right-hand side of the system
iode.examples.sm (204,21 КиБ) скачан 1606 раз(а).
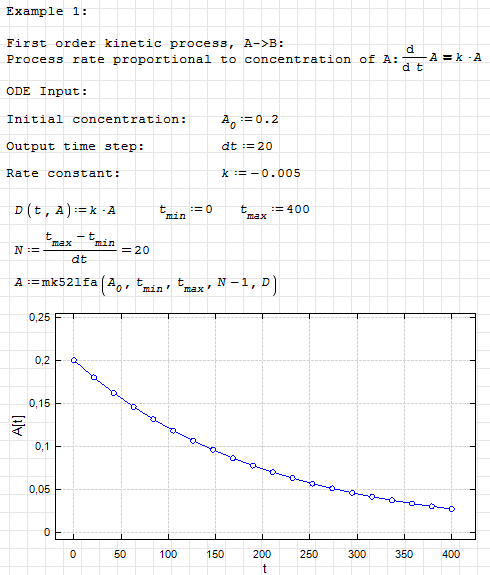
iode.kinetic1.sm (7,75 КиБ) скачан 1502 раз(а).
iode.kinetic2.sm (14,4 КиБ) скачан 1435 раз(а).
iode.kinetic3.sm (14,08 КиБ) скачан 6348 раз(а).
iode.integrate.sm (10,57 КиБ) скачан 6339 раз(а).
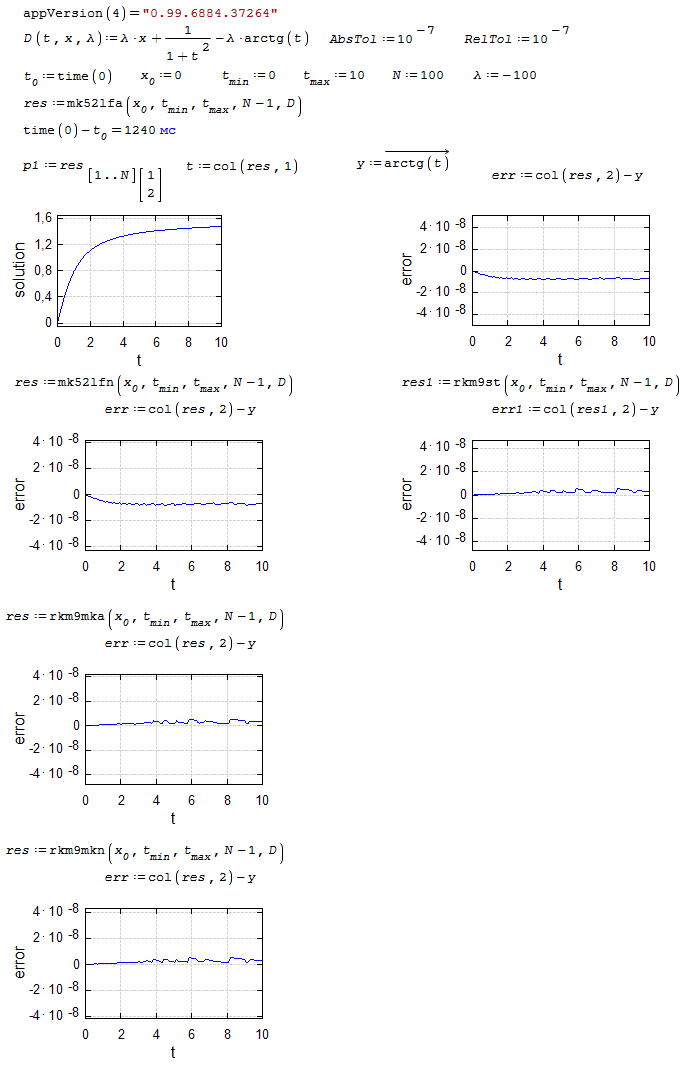
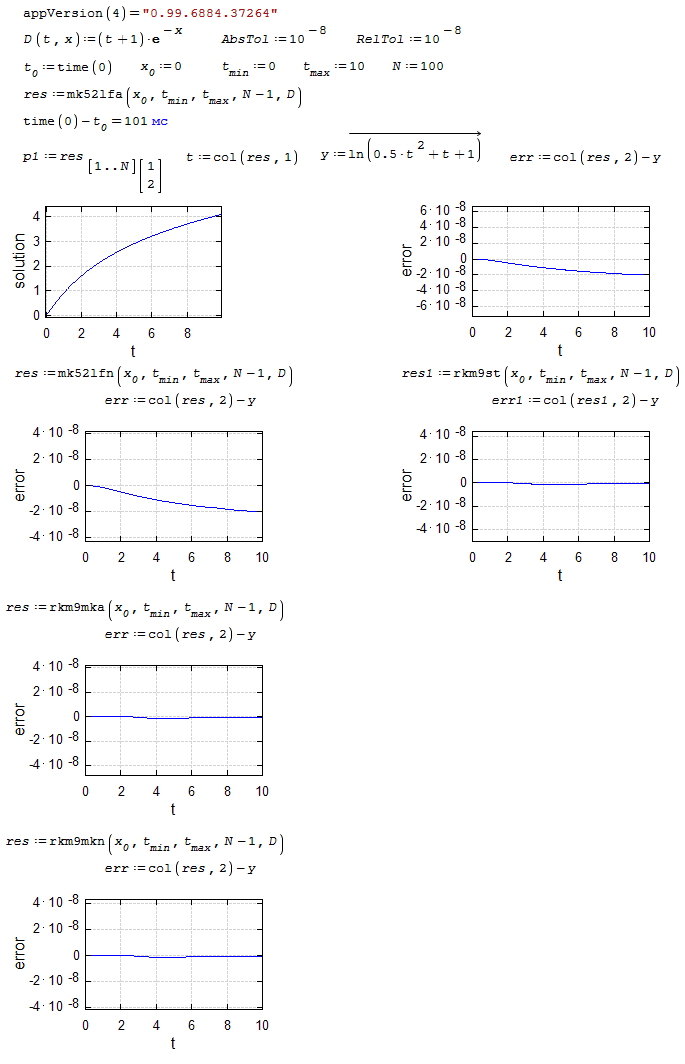
iode.test1.sm (22,49 КиБ) скачан 1429 раз(а).
iode.test2.sm (22,5 КиБ) скачан 1545 раз(а).
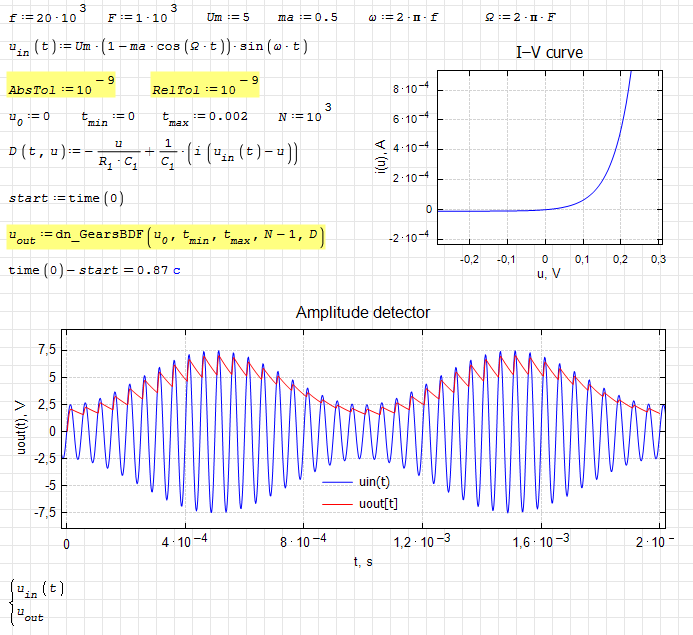
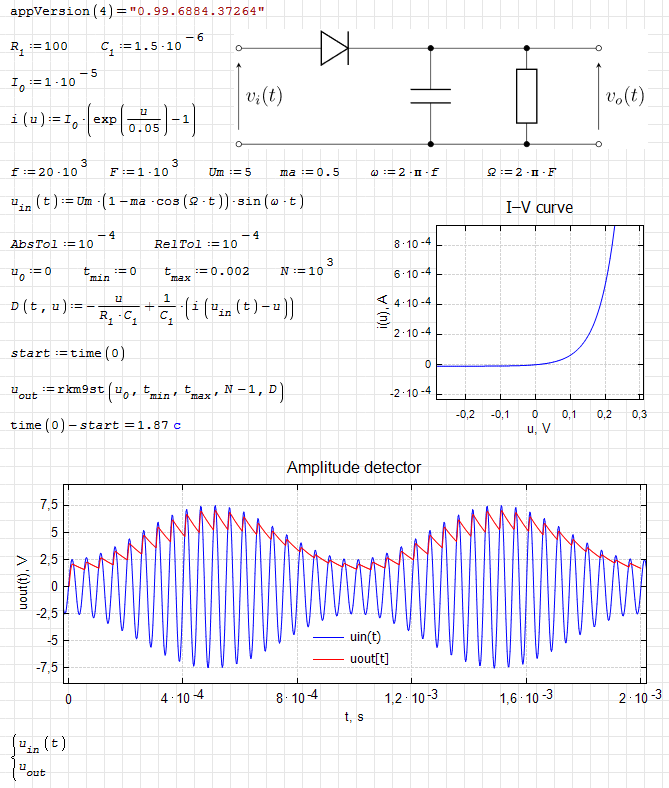
iode.Amplitude detector.sm (20,18 КиБ) скачан 1483 раз(а).
Box_models.sm (100,18 КиБ) скачан 6267 раз(а).
iode.examples.pdf (416,34 КиБ) скачан 801 раз(а).
iode.kinetic1.pdf (74,06 КиБ) скачан 673 раз(а).
iode.kinetic2.pdf (90,4 КиБ) скачан 658 раз(а).
iode.kinetic3.pdf (88,45 КиБ) скачан 627 раз(а).
iode.integrate.pdf (88,91 КиБ) скачан 790 раз(а).
iode.test1.pdf (116,24 КиБ) скачан 670 раз(а).
iode.test2.pdf (121,64 КиБ) скачан 651 раз(а).
iode.Amplitude detector.pdf (147,71 КиБ) скачан 706 раз(а).
Box_models.pdf (145,32 КиБ) скачан 707 раз(а).
Documents:
Intel ODE Solver Library Reference Manual (2018).pdf (239,74 КиБ) скачан 805 раз(а).
See also:
● [topic=726]Mathcad Toolbox[/topic]
● [topic=1918]DotNumerics[/topic]
● [topic=13809]SADEL[/topic]
● [topic=1970]Matlab C++ Math Library[/topic]
● [topic=17063]OSLO[/topic]
● [topic=17067]lsoda[/topic]
● [topic=1997]GNU Scientific Library (GSL)[/topic]






Functions list: rkm9st(5), mk52lfn(5), mk52lfa(5), rkm9mkn(5), rkm9mka(5).
rkm9st(init, x1, x2, intvls, D) A specialized routine for solving non-stiff and middle-stiff ODE systems using the explicit method, which is based on the 4th order Merson’s method and the 1st order multistage method of up to and including 9 stages with stability control.
mk52lfn(init, x1, x2, intvls, D) A specialized routine for solving stiff ODE systems using the implicit method based on L-stable (5,2)-method with the numerical Jacobi matrix, which is computed by the routine.
mk52lfa(init, x1, x2, intvls, D) A specialized routine for solving stiff ODE systems using the implicit method based on L-stable (5,2)-method with numerical or analytical computation of the Jacobi matrix. The user must provide a routine for this computation.
rkm9mkn(init, x1, x2, intvls, D) A specialized routine for solving ODE systems with a variable or a priori unknown stiffness; automatically chooses the explicit or implicit scheme in every step and computes the numerical Jacobi matrix when necessary.
rkm9mka(init, x1, x2, intvls, D) A specialized routine for solving ODE systems with a variable or a priori unknown stiffness; automatically chooses the explicit or implicit scheme in every step. The user must provide a routine for numerical or analytical computation of the Jacobi matrix.
Arguments:
- init is either a vector of n real initial values, where n is the number of unknowns (or a single scalar initial value, in the case of a single ODE).
- x1 and x2 are real, scalar endpoints of the interval over which the solution to the ODE(s) is evaluated. Initial values in init are the values of the ODE function(s) evaluated at x1.
- intvls is the integer number of discretization intervals used to interpolate the solution function. The number of solution points is the number of intervals + 1.
- D is a vector function of the form D(x,y) specifying the right-hand side of the system





iode.examples.sm (204,21 КиБ) скачан 1606 раз(а).
iode.kinetic1.sm (7,75 КиБ) скачан 1502 раз(а).
iode.kinetic2.sm (14,4 КиБ) скачан 1435 раз(а).
iode.kinetic3.sm (14,08 КиБ) скачан 6348 раз(а).
iode.integrate.sm (10,57 КиБ) скачан 6339 раз(а).
iode.test1.sm (22,49 КиБ) скачан 1429 раз(а).
iode.test2.sm (22,5 КиБ) скачан 1545 раз(а).
iode.Amplitude detector.sm (20,18 КиБ) скачан 1483 раз(а).
Box_models.sm (100,18 КиБ) скачан 6267 раз(а).
iode.examples.pdf (416,34 КиБ) скачан 801 раз(а).
iode.kinetic1.pdf (74,06 КиБ) скачан 673 раз(а).
iode.kinetic2.pdf (90,4 КиБ) скачан 658 раз(а).
iode.kinetic3.pdf (88,45 КиБ) скачан 627 раз(а).
iode.integrate.pdf (88,91 КиБ) скачан 790 раз(а).
iode.test1.pdf (116,24 КиБ) скачан 670 раз(а).
iode.test2.pdf (121,64 КиБ) скачан 651 раз(а).
iode.Amplitude detector.pdf (147,71 КиБ) скачан 706 раз(а).
Box_models.pdf (145,32 КиБ) скачан 707 раз(а).
Documents:
Intel ODE Solver Library Reference Manual (2018).pdf (239,74 КиБ) скачан 805 раз(а).
See also:
● [topic=726]Mathcad Toolbox[/topic]
● [topic=1918]DotNumerics[/topic]
● [topic=13809]SADEL[/topic]
● [topic=1970]Matlab C++ Math Library[/topic]
● [topic=17063]OSLO[/topic]
● [topic=17067]lsoda[/topic]
● [topic=1997]GNU Scientific Library (GSL)[/topic]
Russia ☭ forever, Viacheslav N. Mezentsev
3 пользователям понравился этот пост
NDTM Amarasekera 01.02.2019 01:43:00, Davide Carpi 01.02.2019 10:56:00, Radovan Omorjan 01.02.2019 15:35:00
325 сообщений из 2 052 понравились и 1 не понравились пользователям.
Группа: Moderator
Hmm...even dn_GearsBDF() will go nuts for this example.
Just for the record...
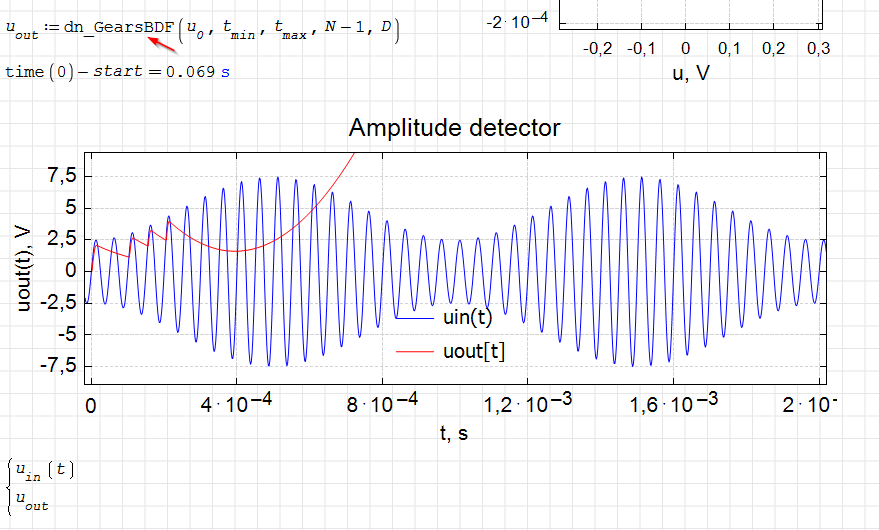
iode.Amplitude detector-1.sm (19,9 КиБ) скачан 3603 раз(а).
EDIT: mk52lfa() and mk52lfn() will also perform well here
Just for the record...

iode.Amplitude detector-1.sm (19,9 КиБ) скачан 3603 раз(а).
EDIT: mk52lfa() and mk52lfn() will also perform well here
When Sisyphus climbed to the top of a hill, they said: "Wrong boulder!"
WroteHmm...even dn_GearsBDF() will go nuts for this example.
From recollection,NONE ODE solve that one.
Cheers ... Jean.
ODE rkfixed Pulse Pitfall.sm (37,2 КиБ) скачан 1263 раз(а).
325 сообщений из 2 052 понравились и 1 не понравились пользователям.
Группа: Moderator
I should have guessed that  . Thank you.
. Thank you.
When Sisyphus climbed to the top of a hill, they said: "Wrong boulder!"
2 пользователям понравился этот пост

Plugin updated.
Changes:
- solution restructured;
- converting the task for the ODE solver to the numerical form is now performed through the Mathcad Toolbox plugin (to avoid code duplication), so it must be installed;
- refactored.
Solvers that support mathematical notation now reuse code from the Mathcad Toolbox plugin. Now there is no need to recompile every such plugin.
Russia ☭ forever, Viacheslav N. Mezentsev
1 страниц (7 вхождений)
- Новые сообщения
- Нет новых сообщений