This was mentioned on another thread regarding small numbers. Adding two small numbers will cause an error with a rather confusing message (result is above max. positive allowed number???).



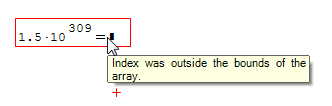
There should not be an error but either zero or 1.5e-115 as a result. It is even mentioned in this post that the last working version was 0.99.6824. I believe that some binary arithmetic fails here.

Regards,
Radovan

Wrote

This was mentioned on another thread regarding small numbers. Adding two small numbers will cause an error with a rather confusing message (result is above max. positive allowed number???).



There should not be an error but either zero or 1.5e-115 as a result. It is even mentioned in this post that the last working version was 0.99.6824. I believe that some binary arithmetic fails here.

Regards,
Radovan

You are right Radovan, this should be a bug. I have checked the addition on old versions.
0.99.7016 (and older versions) can calculate the mentioned additon, 0.99.7100 and after doesn't.

Let me clarify something, exp(709.783) is still not calculated on 0.99.6824 too.
But somehow the Project Fission.sm calculations can be done with 0.99.6824.

As I said on other thread, there are some serious issues over here.

Regards

Wrote

...I have checked the addition on old versions.
0.99.7016 (and older versions) can calculate the mentioned additon, 0.99.7100 and after doesn't.

Let me clarify something, exp(709.783) is still not calculated on 0.99.6824 too.
But somehow the Project Fission.sm calculations can be done with 0.99.6824.

As I said on other thread, there are some serious issues over here.

Regards

I agree and thank you for checking.

Regards,
Radovan

Wrote

There should not be an error but either zero or 1.5e-115 as a result. It is even mentioned in this post that the last working version was 0.99.6824. I believe that some binary arithmetic fails here.

For sure 7109 is freaked, not yet doctored.

Wrote

For sure 7109 is freaked, not yet doctored.

As it looks, 7109 has been deeply victimized.
Something like the American credit card Capital One [109 000 000 victims]
Quebec taxation ministry [30 000 victims]
Another Quebec bank [9 000 000 victims]

This error message is also confusing (Numeric optimization of the region).



Why some array and what index is mentioned here?

Regards,
Radovan

Wrote

This error message is also confusing (Numeric optimization of the region).



Why some array and what index is mentioned here?

Regards,
Radovan

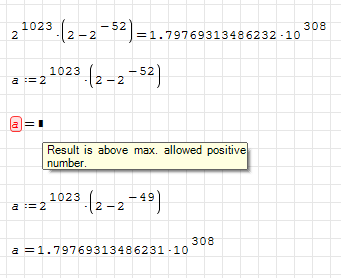
The error message is wrong here. Actually the number is bigger than
maximum value of IEEE 754 double-precision standard (binary64) capability.
This is why we are getting an error. (the error should be overflow, not array or index)
http://en.wikipedia.org/wiki/Double-precision_floating-point_format

Which is;

2^1023*(2-2^(-52))=1.79769313486232*10^308

If Smath can be recoded with IEEE 754 Octuple-precision (binary256) maximum value could be;

2^262143*(2−2^(−236))=1.61132571748576047361957211845200501064402387454966951747637125049607182699*10^78913

Regards

What I couldn't understand why Smath is giving the error below?
Maximum value of IEEE754 binary64 can be calculated and shown on its own.
But why do I get an error if maximum (or minimum) value is assigned to a variable?



Regards

As we mentionded here many times, SMath always had some serious problems with its core symbolic/numeric engine. Therefore different Optimizations introduced to overcome these problems etc. The problems still remained or reappeared here and there. See this mentioned simple example with different Optimizations.



optim.sm (6 КиБ) скачан 30 раз(а).

Regards,
Radovan

1.5*10^309 is above 32 bit floating ^307
SS 6179 replies otherwise "Result above max allowed positive number"
"Index above the bounds of the array" is seemingly Windows message.
The function is the power function Y^X built-in at machine code level.
As it looks: they call the machine code suite "array" associated with
an "index" executing that suite ???
Radovan, your work hard !
Cheers ... Jean

Wrote

What I couldn't understand why Smath is giving the error below?
Maximum value of IEEE754 binary64 can be calculated and shown on its own.
But why do I get an error if maximum (or minimum) value is assigned to a variable?

Answer is in some ways here, attached.
Functions don't exist in computing machinery. They are machine code from Windows,
from the Padé rational fraction [Hart et al.] 4 arithmetic operations[+,-,*,/].
Their rating is 21 digits floating point -3 uncertain floating digits.
Only 15 are conserved [Excel, Mathcad, Smath ...] taking into account error
propagation from projects and by agreed convention.
As it looks/demonstrated attached, Smath replaces digits above 15 by '0'.
That may not be correct in some ways ?

All that stuff 64 floating point is purely useless for PC on the account
of the explained above. It has surely interest for parallel computing
capable of displaying > 15 digits. No interest for Engineering project.
Attached MCD is from XP Pro. 64 bits floating point. It points the > 307.
Most interesting but NOT that many adepts.

On the other hand, it bother my Thiele as they have to be expanded
via maple. Some coefficients are so long that they can't be evaluated.
I'm thus forced to run in MCD for evaluation.

Just to get back to the more problematic thing here. The edge of the big numbers is not so problematic as the edge of the numbers close to zero (IMHO).

The main problem here is with the rather small numbers close to zero. I think that lots of calculations will fail if we deal with the numbers which have practically zero values because of the errors SMath will popup and stop calculations. I think this behavior can not be acceptable.

Unfortunately, no answers yet about this problem

Regards,
Radovan

There is no difference in the presentation of large and small numbers. To represent a large number, you need one long integer ( a/1 ). To represent a small number, you need long integer ( 1/a ). The problem is long integers, i.e. large numbers. It's all about this: С ⊂ Q ⊂ Z, there C - complex numbers, Q - rational numbers, Z - integers. So, if you have any number as symbolic expression this number is complex number represented with real and image parts as rational numbers represented as big integers. I don't know how it works in SMath Studio, but in Tiny.Science all numbers based on long integers. And a small number is a big number x in equation 1/x.

Wrote

Just to get back to the more problematic thing here. The edge of the big numbers is not so problematic as the edge of the numbers close to zero (IMHO).

The main problem here is with the rather small numbers close to zero. I think that lots of calculations will fail if we deal with the numbers which have practically zero values because of the errors SMath will popup and stop calculations. I think this behavior can not be acceptable.

Unfortunately, no answers yet about this problem

I have recollection [1990] zero was defined value ≤ 10e-12=0
Today is not so and anything from anything that calculates.

Mathcad 11 [2003] XP Pro ...
1.7976931348623157*10^-15 = 1.7976931348623157*10^-15
1.7976931348623157*10^-16 = 0.000000000000000

Smath result below may mean something but not to me ≤ e-15
e-15 is only few layers of hydrogen atom at top of 1 km tower,
i.e: not measurable.

Cheers ... Jean

Some more weird things regarding the presentation of numbers and optimization in SMath



I agree with uni that both internal presentations of small and big numbers are equally important but SMath is obviously doing something wrong.

Regards,
Radovan

Wrote

I agree with uni that both internal presentations of small and big numbers are equally important but SMath is obviously doing something wrong.

Floating point arithmetic floats in uncertainty.
That's why all functions rated 21 decimals are truncated to 15 display.
Cody Junior has a long explanation on that with different machines.
The book in question is ~ 1990 or before.

1.976262583364990/1.7976931348623157=1.09933255294784

Unfortunately, my question still remained unanswered. Is this going to stay this way or is there any chance of changing this somehow in SMath?

Regards,
Radovan

Wrote

Unfortunately, my question still remained unanswered. Is this going to stay this way or is there any chance of changing this somehow in SMath?

I think we might try to capture the exception and return a "full 0" for such cases. To be inspected since different optimizations works in different ways (nice catches Radovan).

Wrote

Wrote

Unfortunately, my question still remained unanswered. Is this going to stay this way or is there any chance of changing this somehow in SMath?

I think we might try to capture the exception and return a "full 0" for such cases. To be inspected since different optimizations works in different ways (nice catches Radovan).

Thank you Davide for your answer and the confirmation that there is actually a problem I suppose.

Regards,
Radovan

Wrote

I think we might try to capture the exception and return a "full 0" for such cases. To be inspected since different optimizations works in different ways (nice catches Radovan).

Thanks Davide for attending our distress !
The problem appeared in the Fission project SS 7019 few weeks ago.
Project turned red in the Originator document, but fine SS 6179.
Mathematica 4.0 had NaN
Mathcad 11.2a implemented NaN at design time of DAEP [2003]

Jean



Maths Overflow [Max above limit].sm (47 КиБ) скачан 35 раз(а).
Project Fission.sm (187 КиБ) скачан 35 раз(а).