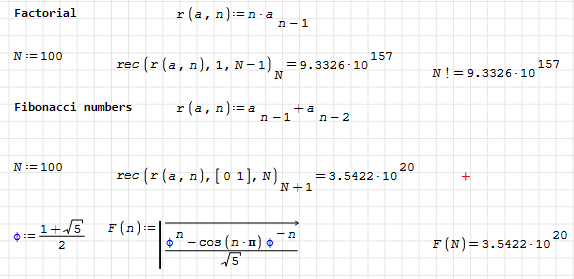1 страниц (16 вхождений)
Recursion in SMath - Can we use recursion in SMath? - Сообщения
Yes, recursion is possible. Although I don't remember how many levels are allowed.
Here is your example in an smath file.
Fibo_recursion_example.sm (3,56 КиБ) скачан 948 раз(а).
Here is your example in an smath file.
Fibo_recursion_example.sm (3,56 КиБ) скачан 948 раз(а).
1 пользователям понравился этот пост
Valery Ochkov 24.10.2023 16:48:00
WroteYes, recursion is possible. Although I don't remember how many levels are allowed.
Here is your example in an smath file.
Fibo_recursion_example.sm (3,56 КиБ) скачан 948 раз(а).
Thanks! But I think it was not from me but from SMath error!
And the second!
Why 0!=1?
See
Factorial.sm (4,45 КиБ) скачан 913 раз(а).

Here is the corrected Fibo recursive function...
Fibo_recursion_corrected.sm (4,21 КиБ) скачан 924 раз(а).
As for 0!=1 the following page gives two explanations.
https://zero-factorial.com/whatis.html
Fibo_recursion_corrected.sm (4,21 КиБ) скачан 924 раз(а).
As for 0!=1 the following page gives two explanations.
https://zero-factorial.com/whatis.html
Here is a more streamlined version...

1 пользователям понравился этот пост
Valery Ochkov 24.10.2023 20:50:00
WroteHere is a more streamlined version...
Thanks!
And what about
https://en.wikipedia.org/wiki/Ackermann_function
WroteYes, recursion is possible. Although I don't remember how many levels are allowed.
Typical, factorial(n) command-line is limited ...factorial(40)
1 пользователям понравился этот пост
Valery Ochkov 25.10.2023 20:46:00
WroteOriginally Posted by: Gerry_Bush [url=/forum/yaf_postsm82817_Recursion-in-SMath.aspx#post82817][/url]Yes, recursion is possible. Although I don't remember how many levels are allowed.
Typical, factorial(n) command-line is limited ...factorial(40)
By same token, Fibonacci(n) command-line upper limit
Fibonacci(1473) ... 1.9069*10^307 ... Windows limit.
1 пользователям понравился этот пост
Valery Ochkov 26.10.2023 00:49:00
2 пользователям понравился этот пост
4 пользователям понравился этот пост
ioan92 26.10.2023 00:28:00, Valery Ochkov 25.10.2023 23:27:00, NDTM Amarasekera 25.10.2023 23:53:00, Oscar Campo 26.10.2023 16:39:00
WroteTypical, factorial(n) command-line is limited ...factorial(40)
The vectorized version n 170 ... 7.2574*10^306
1 пользователям понравился этот пост
Valery Ochkov 26.10.2023 00:49:00
2 пользователям понравился этот пост
Valery, Smath Gamma(x) is known 4 decimals.
Reported years ago, ignored.
Alvaro Gamma(x) 15 decimals
Reported years ago, ignored.
Alvaro Gamma(x) 15 decimals
Wrote... And what about
https://en.wikipedia.org/wiki/Ackermann_function
Ackermann function is not 'primitive recursive', which means that it can't be computed only with for loops. Here an iterative implementation with a stack and no recursion.
Ackermann-Iterative.sm (8,7 КиБ) скачан 892 раз(а).
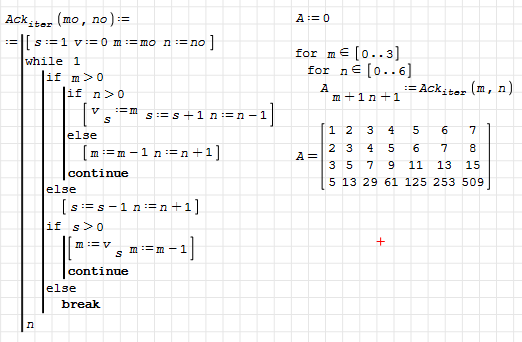
Best regards.
Alvaro.
2 пользователям понравился этот пост
1 страниц (16 вхождений)
- Новые сообщения
- Нет новых сообщений