SADEL - Sets of Algebraic and Differential Equations solvers Library (SADEL) - Сообщения
SADEL





Functions list: manzhuk(5|6|7)
DAE (ODE) solvers:
manzhuk(init, x1, x2, intvls, D)
Arguments:
- init is either a vector of n real initial values, where n is the number of unknowns (or a single scalar initial value, in the case of a single ODE).
- x1 and x2 are real, scalar endpoints of the interval over which the solution to the ODE(s) is evaluated. Initial values in init are the values of the ODE function(s) evaluated at x1.
- intvls is the integer number of discretization intervals used to interpolate the solution function. The number of solution points is the number of intervals + 1.
- D is a vector function of the form D(x,y) specifying the right-hand side of the system
manzhuk(init, x1, x2, intvls, G, J1)
manzhuk(init, x1, x2, intvls, G, J1, J2)
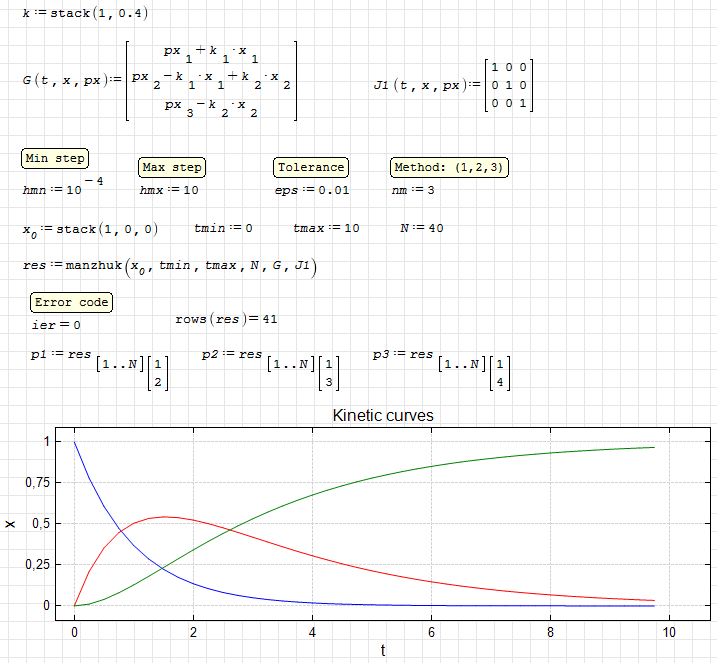

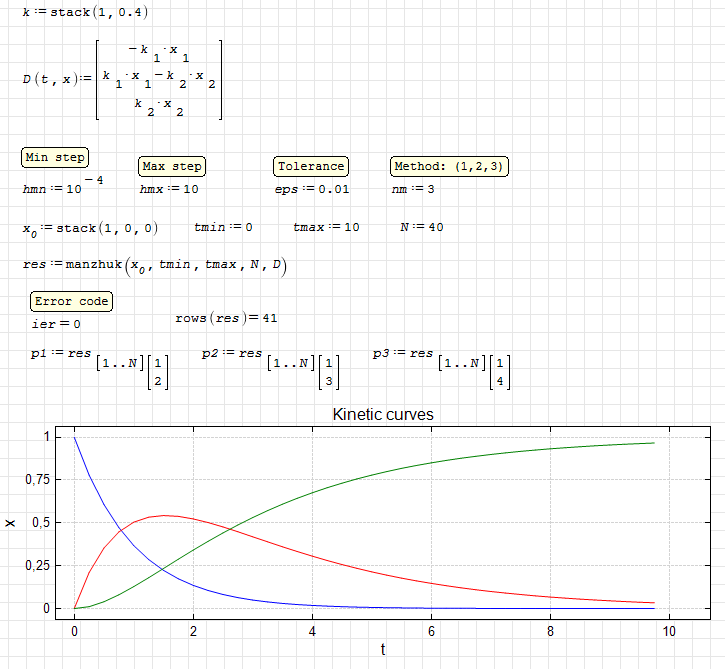
manzhuk. Kinetic curves.sm (13,02 КиБ) скачан 1066 раз(а).
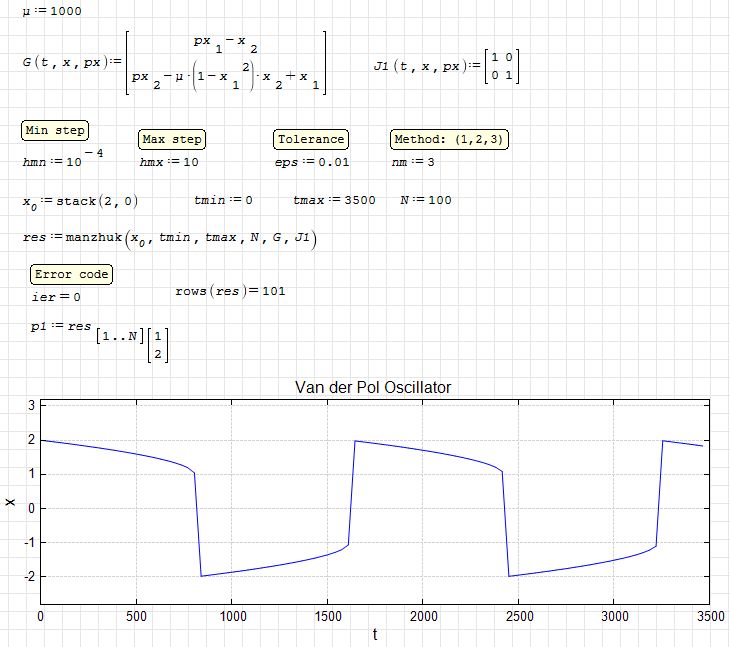
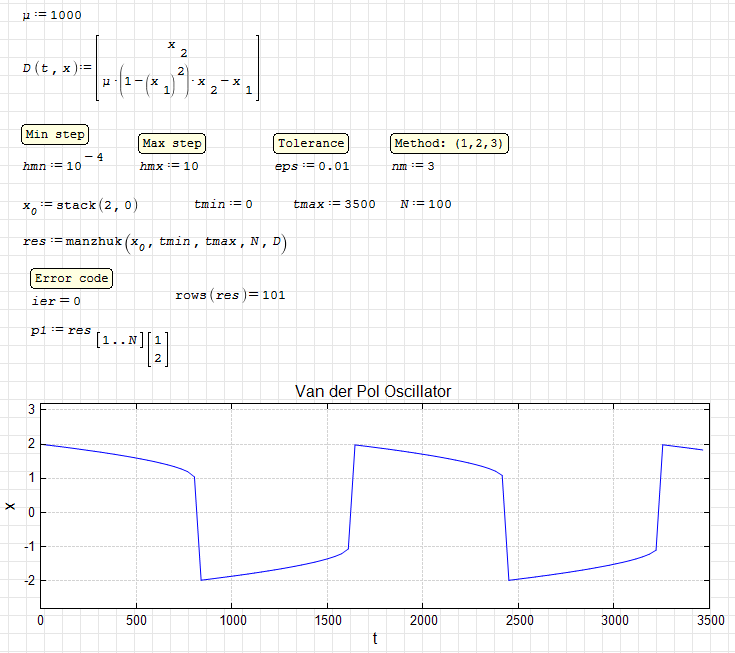
manzhuk. Van der Pol oscillator 1.sm (10,4 КиБ) скачан 1088 раз(а).
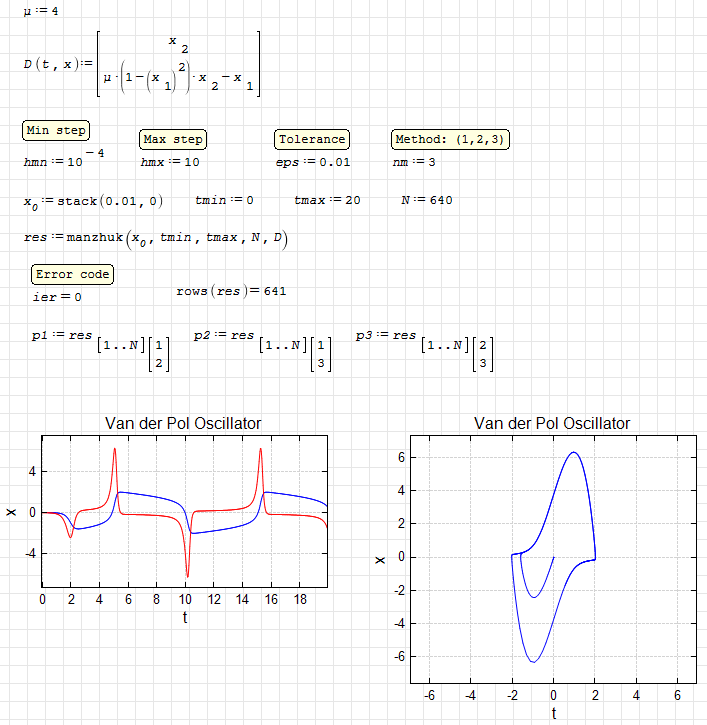
manzhuk. Van der Pol oscillator 2.sm (13,47 КиБ) скачан 1088 раз(а).
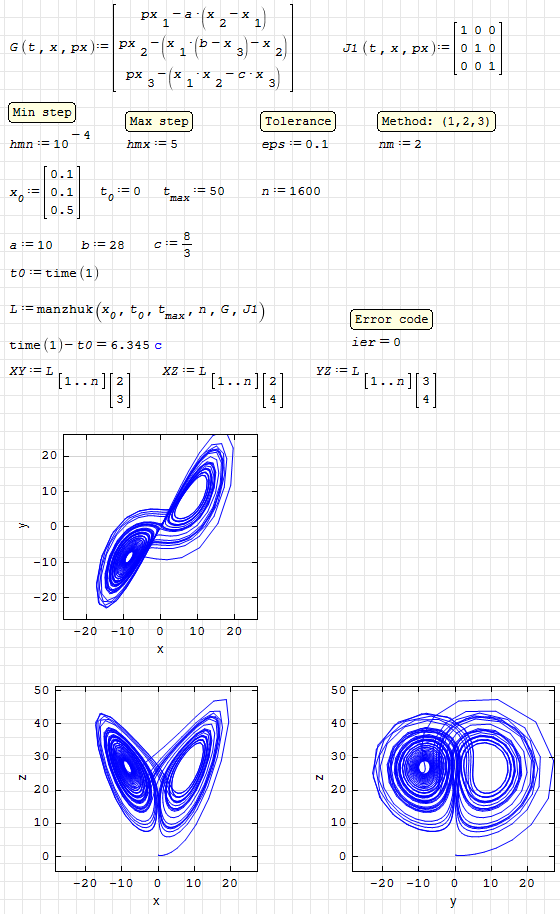
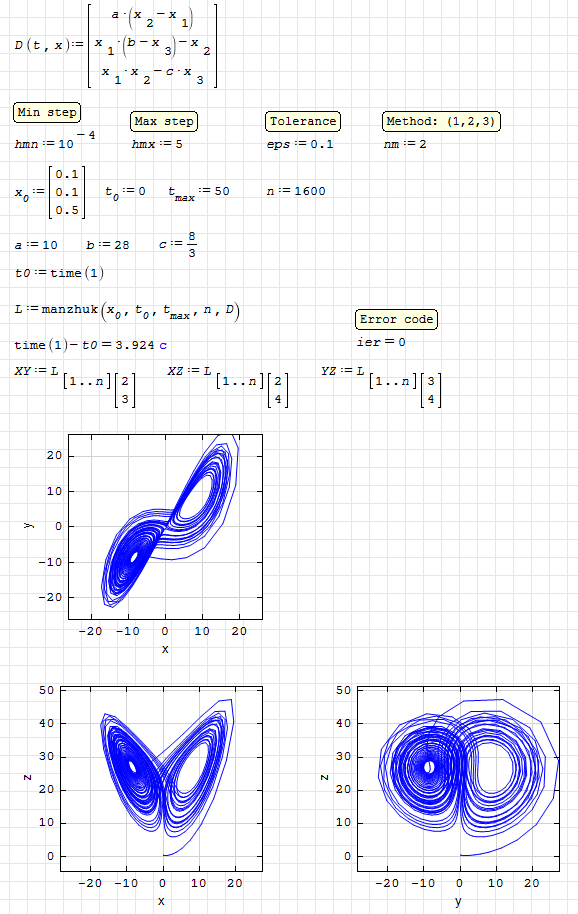
manzhuk. Lorenz-Attractor.sm (16,83 КиБ) скачан 1083 раз(а).
manzhuk. Kinetic curves.pdf (38,39 КиБ) скачан 542 раз(а).
manzhuk. Van der Pol oscillator 1.pdf (46,19 КиБ) скачан 518 раз(а).
manzhuk. Van der Pol oscillator 2.pdf (62,1 КиБ) скачан 514 раз(а).
manzhuk. Lorenz-Attractor.pdf (65,71 КиБ) скачан 557 раз(а).
Manual (rus): DAE-solver-manzhuk.pdf (3,41 МиБ) скачан 623 раз(а).
Links:
1. SADEL.





Functions list: manzhuk(5|6|7)
DAE (ODE) solvers:
manzhuk(init, x1, x2, intvls, D)
Arguments:
- init is either a vector of n real initial values, where n is the number of unknowns (or a single scalar initial value, in the case of a single ODE).
- x1 and x2 are real, scalar endpoints of the interval over which the solution to the ODE(s) is evaluated. Initial values in init are the values of the ODE function(s) evaluated at x1.
- intvls is the integer number of discretization intervals used to interpolate the solution function. The number of solution points is the number of intervals + 1.
- D is a vector function of the form D(x,y) specifying the right-hand side of the system
manzhuk(init, x1, x2, intvls, G, J1)
manzhuk(init, x1, x2, intvls, G, J1, J2)




manzhuk. Kinetic curves.sm (13,02 КиБ) скачан 1066 раз(а).
manzhuk. Van der Pol oscillator 1.sm (10,4 КиБ) скачан 1088 раз(а).
manzhuk. Van der Pol oscillator 2.sm (13,47 КиБ) скачан 1088 раз(а).
manzhuk. Lorenz-Attractor.sm (16,83 КиБ) скачан 1083 раз(а).
manzhuk. Kinetic curves.pdf (38,39 КиБ) скачан 542 раз(а).
manzhuk. Van der Pol oscillator 1.pdf (46,19 КиБ) скачан 518 раз(а).
manzhuk. Van der Pol oscillator 2.pdf (62,1 КиБ) скачан 514 раз(а).
manzhuk. Lorenz-Attractor.pdf (65,71 КиБ) скачан 557 раз(а).
Manual (rus): DAE-solver-manzhuk.pdf (3,41 МиБ) скачан 623 раз(а).
Links:
1. SADEL.
Russia ☭ forever, Viacheslav N. Mezentsev
5 пользователям понравился этот пост
frapuano 21.07.2018 15:14:00, Radovan Omorjan 21.07.2018 15:15:00, NDTM Amarasekera 21.07.2018 16:21:00, Davide Carpi 23.07.2018 06:23:00, Andrey Ivashov 07.12.2018 17:22:00
Updated. Short form added.
manzhuk. Kinetic curves (short).sm (11,78 КиБ) скачан 1141 раз(а).
manzhuk. Lorenz-Attractor (short).sm (15,49 КиБ) скачан 1081 раз(а).
manzhuk. Van der Pol oscillator 1 (short).sm (9,47 КиБ) скачан 1078 раз(а).
manzhuk. Van der Pol oscillator 2 (short).sm (12,54 КиБ) скачан 1067 раз(а).
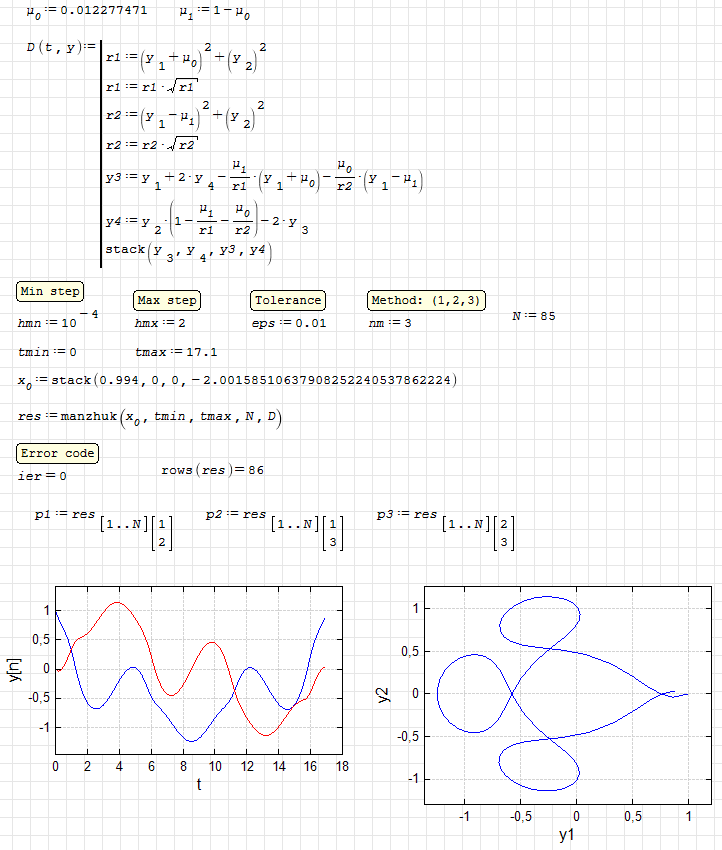
manzhuk. Arenstorf Orbit (short).sm (16,28 КиБ) скачан 1028 раз(а).
manzhuk. Kinetic curves (short).pdf (37,25 КиБ) скачан 554 раз(а).
manzhuk. Lorenz-Attractor (short).pdf (63,85 КиБ) скачан 555 раз(а).
manzhuk. Van der Pol oscillator 1 (short).pdf (45,71 КиБ) скачан 547 раз(а).
manzhuk. Van der Pol oscillator 2 (short).pdf (61,61 КиБ) скачан 553 раз(а).
manzhuk. Arenstorf Orbit (short).pdf (55,4 КиБ) скачан 541 раз(а).





manzhuk. Kinetic curves (short).sm (11,78 КиБ) скачан 1141 раз(а).
manzhuk. Lorenz-Attractor (short).sm (15,49 КиБ) скачан 1081 раз(а).
manzhuk. Van der Pol oscillator 1 (short).sm (9,47 КиБ) скачан 1078 раз(а).
manzhuk. Van der Pol oscillator 2 (short).sm (12,54 КиБ) скачан 1067 раз(а).
manzhuk. Arenstorf Orbit (short).sm (16,28 КиБ) скачан 1028 раз(а).
manzhuk. Kinetic curves (short).pdf (37,25 КиБ) скачан 554 раз(а).
manzhuk. Lorenz-Attractor (short).pdf (63,85 КиБ) скачан 555 раз(а).
manzhuk. Van der Pol oscillator 1 (short).pdf (45,71 КиБ) скачан 547 раз(а).
manzhuk. Van der Pol oscillator 2 (short).pdf (61,61 КиБ) скачан 553 раз(а).
manzhuk. Arenstorf Orbit (short).pdf (55,4 КиБ) скачан 541 раз(а).
Russia ☭ forever, Viacheslav N. Mezentsev
2 пользователям понравился этот пост
Updated. manzhuk() now more stable. Don't use hmx parameter. By default, its value is dt / 2.
Russia ☭ forever, Viacheslav N. Mezentsev
1 пользователям понравился этот пост
frapuano 22.07.2018 16:55:00
WroteUpdated. Short form added.
Thanks Uni.
The complete Smath code might be educative.
mwode45 solves as well.
Jean
ODE manzhuk Arenstorf Orbit.sm (21,4 КиБ) скачан 1105 раз(а).
325 сообщений из 2 052 понравились и 1 не понравились пользователям.
Группа: Moderator
Hello uni,
It seems this is a quite interesting ODE-DAE solver. I did not understand what the matrices J1 and J2 are. The manual is quite complicated for me. I just supposed that J1,J2 have something to do with DAE (differential algebraic equations). It seems to me that J1 is the Jacobian matrix regarding the vector of parameters (third argument in the function G()). I suppose J2 is again some kind of Jacobian matrix.
If one of your motivation was to have a DAE solver in SMath, I appreciate that very much.
Looking forward for some more examples from you about using this solver - especially DAE systems.
Regards,
Radovan
It seems this is a quite interesting ODE-DAE solver. I did not understand what the matrices J1 and J2 are. The manual is quite complicated for me. I just supposed that J1,J2 have something to do with DAE (differential algebraic equations). It seems to me that J1 is the Jacobian matrix regarding the vector of parameters (third argument in the function G()). I suppose J2 is again some kind of Jacobian matrix.
If one of your motivation was to have a DAE solver in SMath, I appreciate that very much.
Looking forward for some more examples from you about using this solver - especially DAE systems.
Regards,
Radovan
When Sisyphus climbed to the top of a hill, they said: "Wrong boulder!"
3 пользователям понравился этот пост
I have more than 12 examples of how to use it, but, unfortunately, symbolic interpreter slows down the computation of the algorithm. So I decided to show an alternative version of its use, using the Script component. I hope that I will succeed.
Russia ☭ forever, Viacheslav N. Mezentsev
2 пользователям понравился этот пост
Simple test 1.
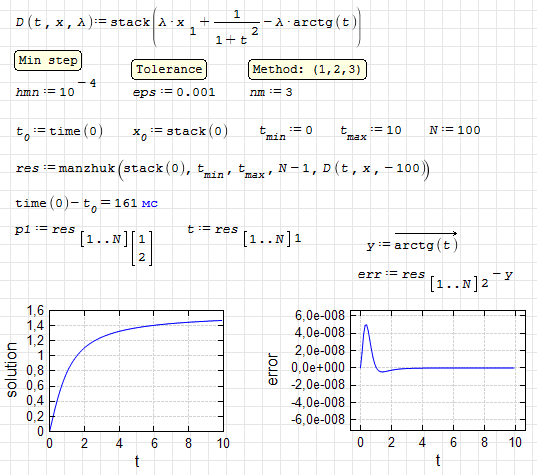
manzhuk.test1.sm (11,8 КиБ) скачан 1083 раз(а).
manzhuk.test1.pdf (48,78 КиБ) скачан 532 раз(а).

manzhuk.test1.sm (11,8 КиБ) скачан 1083 раз(а).
manzhuk.test1.pdf (48,78 КиБ) скачан 532 раз(а).
Russia ☭ forever, Viacheslav N. Mezentsev
1 пользователям понравился этот пост
frapuano 01.08.2018 13:57:00
Updated.
Changes:
- zero point issue partially fixed;
- added support for the simple D(t,x) definition.
Changes:
- zero point issue partially fixed;
- added support for the simple D(t,x) definition.
Russia ☭ forever, Viacheslav N. Mezentsev
Good afternoon!
I use sadel to calculate the parameters of the transient in the RLC-circuit.
Why doesn't time go by in calculations? file attached model2_sadel_p.sm (25,9 КиБ) скачан 1063 раз(а).
I use sadel to calculate the parameters of the transient in the RLC-circuit.
Why doesn't time go by in calculations? file attached model2_sadel_p.sm (25,9 КиБ) скачан 1063 раз(а).
Можно посмотреть на описание задачи в изначальной форме?
Russia ☭ forever, Viacheslav N. Mezentsev
WroteМожно посмотреть на описание задачи в изначальной форме?
Схема замещения https://i.imgur.com/9p8FrH3.png
Система дифуров, описывающая процессы, происходящие при разряде https://i.imgur.com/Qf2fE8w.png
Взаимная индуктивность https://i.imgur.com/lRdX1Hp.png
Входные параметры электрической цепи рассчитаны, но сомнений не вызывают
Для начала нужно в выражении G(t,x,xp) исправить xp на px. Смущает выражение для второй производной. Кажется, что первая и вторая производные dx/dt должны быть как-то связаны. Я не составлял подобных систем и с ходу не могу сказать что не так. Хорошо бы ещё посмотреть на результат моделирования схемы в специализированной программе, чтобы убедиться, что начальные условия и параметры схемы действительно приводят к какому-то не нулевому результату.
Ещё, мне кажется, что не обязательно использовать библиотеку SADEL для решения этой системы, а можно попробовать использовать любые другие решатели, чтобы избавиться от px-параметра.
Ещё, мне кажется, что не обязательно использовать библиотеку SADEL для решения этой системы, а можно попробовать использовать любые другие решатели, чтобы избавиться от px-параметра.
Russia ☭ forever, Viacheslav N. Mezentsev
WroteДля начала нужно в выражении G(t,x,xp) исправить xp на px.
действительно! не заметила. Но конечно это исправление не помогло, программа видимо умнее меня, сама догадалась что имелось ввиду
WroteСмущает выражение для второй производной. Кажется, что первая и вторая производные dx/dt должны быть как-то связаны. Я не составлял подобных систем и с ходу не могу сказать что не так.
dx/dt=v, dv/dt=a. Когда составлялась система дифуров вместо второй производной использовалась первая
WroteХорошо бы ещё посмотреть на результат моделирования схемы в специализированной программе, чтобы убедиться, что начальные условия и параметры схемы действительно приводят к какому-то не нулевому результату.
это хорошая идея, попробую. Просто я опираюсь на источники, где описаны именно такая схема, именно такая система дифуров и именно такие входные параметры. Я пытаюсь пока что просто повторить. Это дает определенную уверенность, что должно работать. Хотя не исключено, что где-то упущена ошибка.
То, что в результатах расчета время не движется - это такая реакция программы на то, что она не может посчитать? Не могу понять о чем это говорит
Нужно, чтобы ier был равен нулю, тогда можно делать интерпретации результата. Этого можно достичь, если исправить указанную ошибку и отключить задание минимального шага интегрирования (hmn) или сделать его меньше. Дальше нужно проверить опечатки в системе. Я посмотрю под отладчиком почему время не меняется.
Russia ☭ forever, Viacheslav N. Mezentsev
WroteМожно писать вот так, чтобы было нагляднее, но промежуточные вычисления в этом случае замедлят работу функции.
вы имеете ввиду нагляднее для того, кто пишет/читает функцию? т.е. другая форма записи?
это здорово - я попробовала так написать, так тоже запускается расчет, правда результат тот же плачевный
По сути это та же форма записи, так как результат работы функции определяется последним выражением блока программы. Определение переменных из вектора k можно вынести из программного блока на лист, т.к. это константы. Ещё нужно всем выражениям указать численный тип оптимизации в свойствах контекстного меню.
Что касается численного моделирования, то можно попробовать посчитать в Proteus данную схемку. Там только нужно подумать как имитировать ключ.
А что за книжка-то?
Что касается численного моделирования, то можно попробовать посчитать в Proteus данную схемку. Там только нужно подумать как имитировать ключ.
А что за книжка-то?
Russia ☭ forever, Viacheslav N. Mezentsev
- Новые сообщения
- Нет новых сообщений