Hello!

Does anybody can explain the result of this expression in wolfram alpha?



Why Amperes are used for both operands in result?

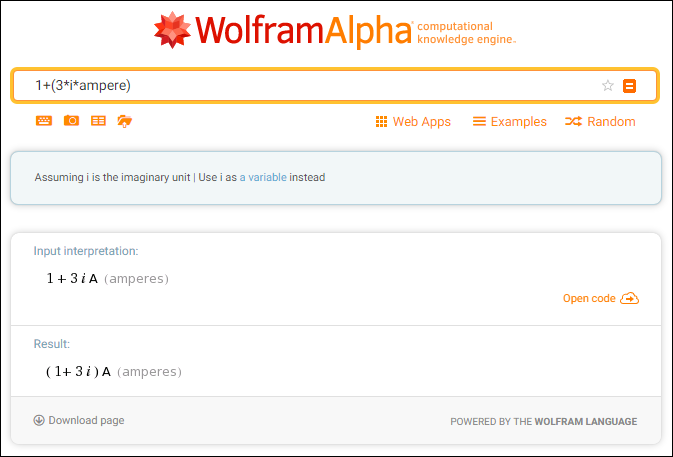
The input expression mixes unitless with units: 1(unitless) + 3i(units A)
so I guess it corrects this by using Amps throughout in the output.
Brian

Andrey, please don't adopt any silent correction behaviour for units in SMath. The rejection of expressions with non-matching units is very helpful.

Wolfram shows that the complex argument is ill posed
if associated with unit. You have it same way in Smath.

Jean

Andrey Wolfram Alpha.sm (4 КиБ) скачан 62 раз(а).

Wrote

Wolfram shows that the complex argument is ill posed
if associated with unit. You have it same way in Smath.

Jean

Neither is the problem ill posed nor is it the same way in SMath. And Wolfram just acts like an over-eager spell-checker with making things worse while trying to make the units match.

If you take i as a variable of dimension 1/A then the units would match. Considering the input being wrong (or ill posed) would require
- i being strictly reserved for sqrt(-1) (which it is not in SMath)
- any variable (like i) being strictly dimensionless (which it is not in SMath)

Obviously both assumptions neither apply to Wolfram Alpha.

The only similarity in the behaviour between SMath and WA is that both assume i being the imaginary unit. Nothing wrong so far.

But is a clear complaint about non-matching units really "the same" as silently messing with the structure of the expression?