1 страниц (9 вхождений)
Hessian - Сообщения
:d
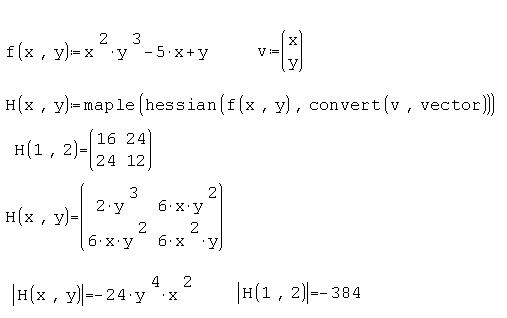
Russia ☭ forever, Viacheslav N. Mezentsev
1 пользователям понравился этот пост
Radovan Omorjan 02.10.2012 03:04:00
I think that this is the better way to work with the Jacobian.
Alvaro.
Jacobian.sm (22,57 КиБ) скачан 1077 раз(а).
Alvaro.
Jacobian.sm (22,57 КиБ) скачан 1077 раз(а).
325 сообщений из 2 052 понравились и 1 не понравились пользователям.
Группа: Moderator
Hello Alvaro,
But what to do if the vector function is defined this way?
[MATH=eng]Φ(X,t):-5*t*mat(el(X,1),el(X,2),2,1)+mat(el(X,2)*el(X,1)^2,el(X,2)^2*el(X,1)^2,2,1)[/MATH]
It will not work until t is a constant (scalar). Take a look at the pictures please.
Regards,
Radovan

But what to do if the vector function is defined this way?
[MATH=eng]Φ(X,t):-5*t*mat(el(X,1),el(X,2),2,1)+mat(el(X,2)*el(X,1)^2,el(X,2)^2*el(X,1)^2,2,1)[/MATH]
It will not work until t is a constant (scalar). Take a look at the pictures please.
Regards,
Radovan

When Sisyphus climbed to the top of a hill, they said: "Wrong boulder!"
325 сообщений из 2 052 понравились и 1 не понравились пользователям.
Группа: Moderator
Hello Alvaro,
Actually, that is the point. I think that's the problem of the symbolic engine.
The first one gives the symbolic result
[MATH=eng](-5*t)*mat(el(X,1),el(X,2),2,1)+mat(el(X,2)*el(X,1)^2,el(X,2)^2*el(X,1),2,1)=mat(-5*el(X,1),-5*el(X,2),2,1)*t+mat(el(X,2)*el(X,1)^2,el(X,2)^2*el(X,1),2,1)[/MATH]
and the result is not a vector, therefore length() does not work.
The second one actually give you the vector symbolically
[MATH=eng](-5)*mat(el(X,1)*t,el(X,2)*t,2,1)+mat(el(X,2)*el(X,1)^2,el(X,2)^2*el(X,1),2,1)=mat(el(X,1)*(-5*t+el(X,2)*el(X,1)),el(X,2)*(-5*t+el(X,2)*el(X,1)),2,1)[/MATH]
Maybe the solution would be to say in advance what the variable t was - either scalar, vector or matrix. Something like "assume". If SMath assumed that t was a scalar, it should behave in accordance to that and give you the second correct result.
Regards,
Radovan
Actually, that is the point. I think that's the problem of the symbolic engine.
The first one gives the symbolic result
[MATH=eng](-5*t)*mat(el(X,1),el(X,2),2,1)+mat(el(X,2)*el(X,1)^2,el(X,2)^2*el(X,1),2,1)=mat(-5*el(X,1),-5*el(X,2),2,1)*t+mat(el(X,2)*el(X,1)^2,el(X,2)^2*el(X,1),2,1)[/MATH]
and the result is not a vector, therefore length() does not work.
The second one actually give you the vector symbolically
[MATH=eng](-5)*mat(el(X,1)*t,el(X,2)*t,2,1)+mat(el(X,2)*el(X,1)^2,el(X,2)^2*el(X,1),2,1)=mat(el(X,1)*(-5*t+el(X,2)*el(X,1)),el(X,2)*(-5*t+el(X,2)*el(X,1)),2,1)[/MATH]
Maybe the solution would be to say in advance what the variable t was - either scalar, vector or matrix. Something like "assume". If SMath assumed that t was a scalar, it should behave in accordance to that and give you the second correct result.
Regards,
Radovan
When Sisyphus climbed to the top of a hill, they said: "Wrong boulder!"
1 страниц (9 вхождений)
- Новые сообщения
- Нет новых сообщений