Animation double pendulum and a pendulum on a spring - Ber7 - Сообщения
#1 Опубликовано: 23.06.2011 10:33:05
https://smath.com/wiki/GetFile.aspx?File=DPendulum.rar
#2 Опубликовано: 23.06.2011 10:35:31
https://smath.com/wiki/GetFile.aspx?File=SwingSpring.rar
#3 Опубликовано: 04.10.2011 23:55:05
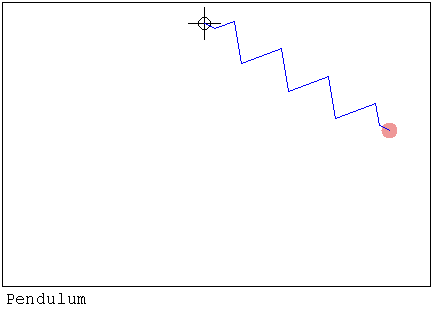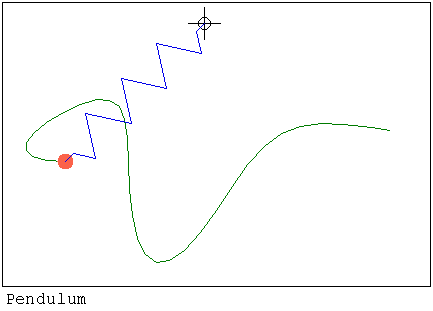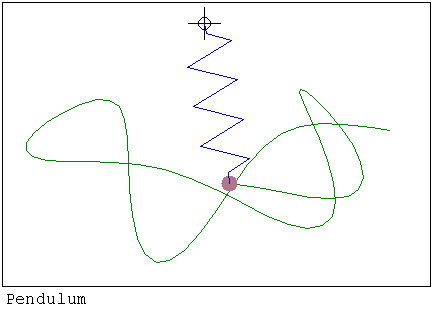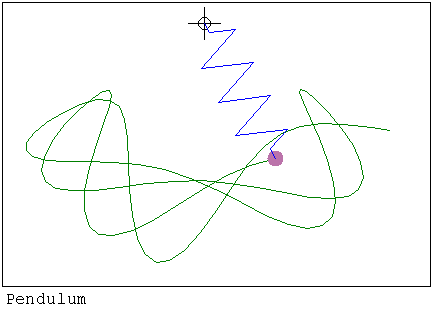
https://smath.com/wiki/GetFile.aspx?File=SwingSpring1.rar
#4 Опубликовано: 05.11.2011 17:42:51
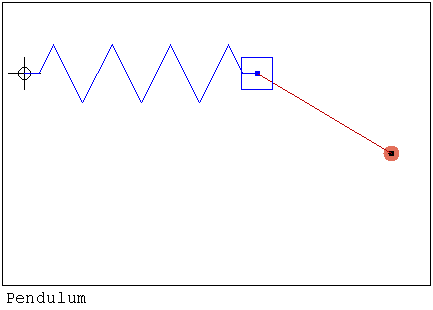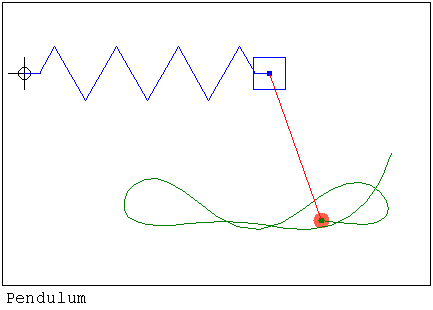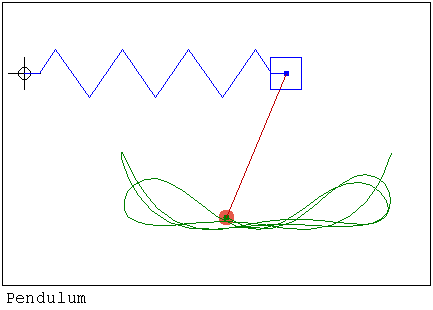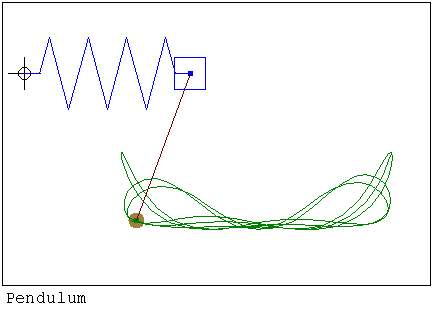
https://smath.com/wiki/GetFile.aspx?File=ElleptPendul.rar
#5 Опубликовано: 22.03.2012 18:38:36
https://smath.com/wiki/GetFile.aspx?File=ElastSuspesion.rar
1 пользователям понравился этот пост
Andrey Ivashov 22.03.2012 20:24:00
#6 Опубликовано: 02.10.2012 23:41:11
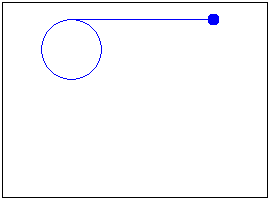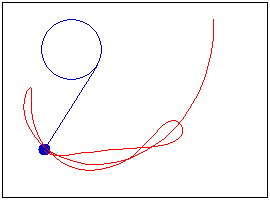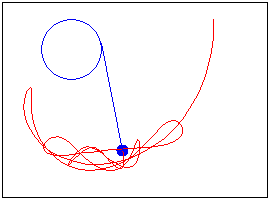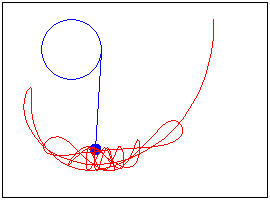
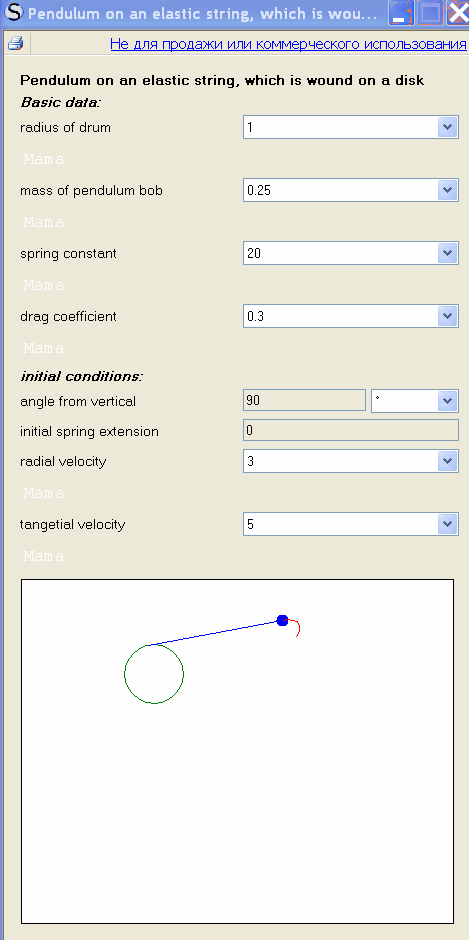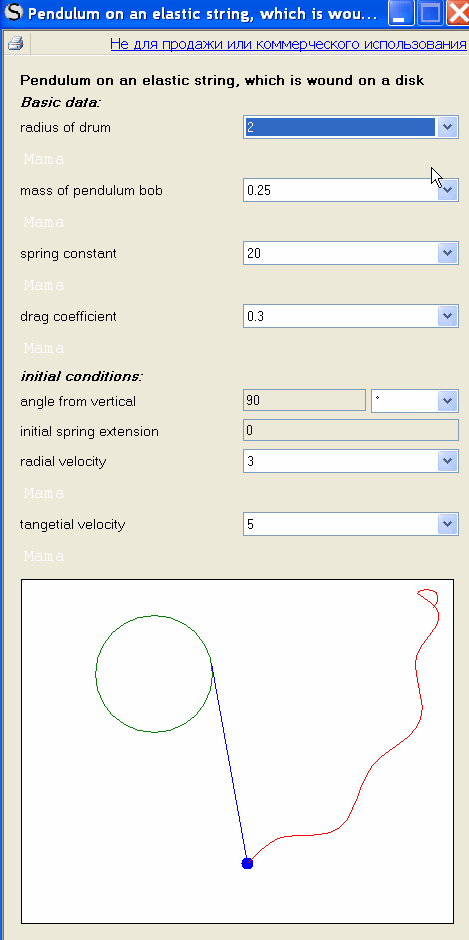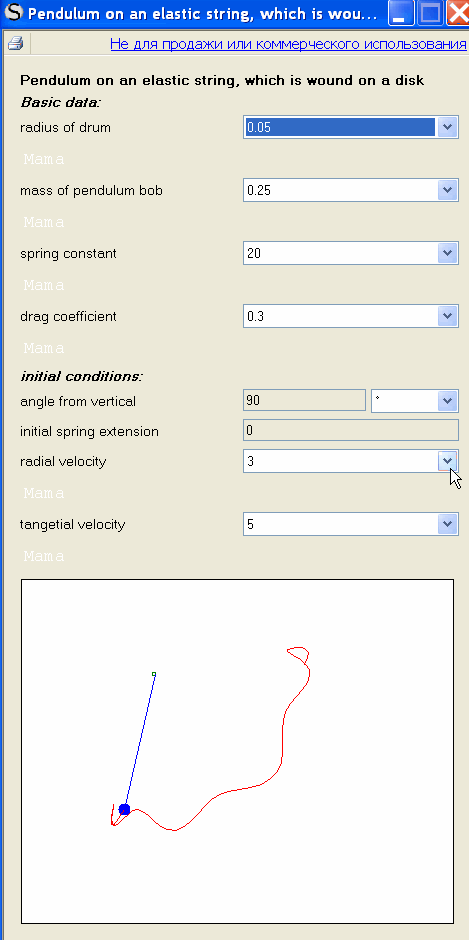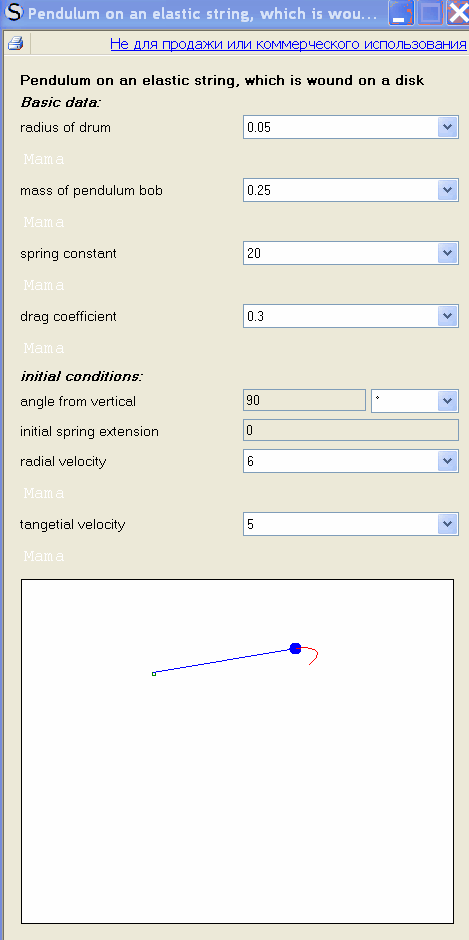
Pendulum on an elastic string, which is wound on a disk
Translated from Mathcad program (the author-Alen Stevens)
http://communities.ptc.com/videos/3335
https://smath.com/wiki/GetFile.aspx?File=ELastPend.rar
Translated from Mathcad program (the author-Alen Stevens)
http://communities.ptc.com/videos/3335
https://smath.com/wiki/GetFile.aspx?File=ELastPend.rar
#7 Опубликовано: 29.05.2013 12:49:49
Crankshaft-Driven Pendulum
The idea is taken from the site http://demonstrations.wolfram.com/CrankshaftDrivenPendulum/
Interactive animation
https://smath.com/wiki/GetFile.aspx?File=PendulKrivExe.rar
PendulKriv1.sm
The idea is taken from the site http://demonstrations.wolfram.com/CrankshaftDrivenPendulum/
Interactive animation
https://smath.com/wiki/GetFile.aspx?File=PendulKrivExe.rar
PendulKriv1.sm
3 пользователям понравился этот пост
#8 Опубликовано: 06.06.2013 08:43:27
Pendulum on an elastic string, which is wound on a disk
Translated from Mathcad program (the author-Alen Stevens)
http://communities.ptc.com/videos/3335
https://smath.com/wiki/GetFile.aspx?File=ELastPend.rar
Interactive animation
https://smath.com/wiki/GetFile.aspx?File=ELastPendExe.rar
2 пользователям понравился этот пост
#9 Опубликовано: 30.07.2013 13:56:21
Rigid rod rocks on a circular surface (Ali H.Nayfeh,Dean T.Mook,Nonlinear Oscillations,1995)
Used an ODE plugin.
rigid1.smz
Used an ODE plugin.
rigid1.smz
2 пользователям понравился этот пост
#10 Опубликовано: 30.07.2013 17:05:22
I 'd propose some adjustments to the functions x(t) and y(t)
[MATH]x(t):eval(r*(sin(θ(t))-θ(t)*cos(θ(t))))[/MATH]
[MATH]y(t):eval(r*(cos(θ(t))+θ(t)*sin(θ(t))))[/MATH]
The differential equation does not account for h, therefore it is correct only for h=0 (rigid bar with no thickness).
rigid1.sm
[MATH]x(t):eval(r*(sin(θ(t))-θ(t)*cos(θ(t))))[/MATH]
[MATH]y(t):eval(r*(cos(θ(t))+θ(t)*sin(θ(t))))[/MATH]
The differential equation does not account for h, therefore it is correct only for h=0 (rigid bar with no thickness).
rigid1.sm
Martin Kraska
Pre-configured portable distribution of SMath Studio: https://en.smath.info/wiki/SMath%20with%20Plugins.ashx
2 пользователям понравился этот пост
#11 Опубликовано: 30.07.2013 19:08:55
Thank you,Martin! Your comments are absolutely correct.
I really made a mistake, you have corrected.
Workheet updated. Thank you again.
Fridel Selitsky.
I really made a mistake, you have corrected.
Workheet updated. Thank you again.
Fridel Selitsky.
1 пользователям понравился этот пост
Davide Carpi 31.07.2013 06:03:00
#12 Опубликовано: 31.07.2013 05:19:31
I should add that the equations of motion of the center of the rod obtained by Martin, are the parametric equations of the involute, which corresponds to the physical meaning of the problem.
1 пользователям понравился этот пост
Davide Carpi 31.07.2013 06:03:00
#13 Опубликовано: 05.08.2013 11:41:35
Fluctuations of three loads
(Ali H.Nayfeh,Dean T.Mook,Nonlinear Oscillations,1995)
The system consists of two extreme loads mass m1 and medium load mass m2 (2m1> m2). If the average load deviate from the equilibrium position, the system begins to oscillate
Blok2.smz
(Ali H.Nayfeh,Dean T.Mook,Nonlinear Oscillations,1995)
The system consists of two extreme loads mass m1 and medium load mass m2 (2m1> m2). If the average load deviate from the equilibrium position, the system begins to oscillate
Blok2.smz
1 пользователям понравился этот пост
Martin Kraska 07.08.2013 07:00:00
#14 Опубликовано: 11.08.2013 12:29:48
Неваляшка(Roly-poly)
The idea is taken from the site
http://demonstrations.wolfram.com/RockingRolyPolyToy/
The center of mass is below the center of rotation of the body
PoluCil1.smz
The idea is taken from the site
http://demonstrations.wolfram.com/RockingRolyPolyToy/
The center of mass is below the center of rotation of the body
PoluCil1.smz
3 пользователям понравился этот пост
Davide Carpi 11.08.2013 12:36:00, Вячеслав Мезенцев 11.08.2013 13:12:00, Martin Kraska 11.08.2013 16:41:00
#16 Опубликовано: 02.09.2013 08:12:56
1 пользователям понравился этот пост
Davide Carpi 02.09.2013 14:09:00
-
Новые сообщения
-
Нет новых сообщений