Temperature units handling - Ioan - Сообщения
#1 Опубликовано: 13.09.2012 16:23:02
Hi all,
It seems to me that the temperature units handling is strange (?)
I attached an example. In engineering it is often used °C unit for the temperature.
Maybe it would useful to use different units for the absolute temperature and for the temperature difference ?
Regards,
Ioan
temperature.sm
It seems to me that the temperature units handling is strange (?)
I attached an example. In engineering it is often used °C unit for the temperature.
Maybe it would useful to use different units for the absolute temperature and for the temperature difference ?
Regards,
Ioan
temperature.sm
#2 Опубликовано: 14.09.2012 00:24:15
Hello Ioan,
here you must use the unit K for temperatur difference, because
alfa is defined as: "change of length [micrometer] per length [m] and per temperstur difference [K]"
Regards,
Peter
here you must use the unit K for temperatur difference, because
alfa is defined as: "change of length [micrometer] per length [m] and per temperstur difference [K]"
Regards,
Peter
#3 Опубликовано: 14.09.2012 03:29:07
Hello Peter,
Thanks for your answer.
I note that in Mathcad, all the situations in my example are accepted because they reserved different unit notation for the absolute temperature and for the temperature change. Why not to do the same for the engineering practical viewpoint?
The temperature change values are the same in °C and K.
Of course the basic SI unit for temperature is the Kelvin and the temptation is to reduce all to K (!?).
Regards,
Ioan
Thanks for your answer.
I note that in Mathcad, all the situations in my example are accepted because they reserved different unit notation for the absolute temperature and for the temperature change. Why not to do the same for the engineering practical viewpoint?
The temperature change values are the same in °C and K.
Of course the basic SI unit for temperature is the Kelvin and the temptation is to reduce all to K (!?).
Regards,
Ioan
#4 Опубликовано: 14.09.2012 03:57:20
Hello Ioan,
if you use °C as unit for the temperature difference, than SMath calculates intenal with unit K.
This is correct.
Because of the definition: 0°C=273.15K a DeltaT of 5°C would be a diff. of 278,15K !
If MathCAD accepts temp. diffs. with unit °C, than that is im my opinion an error (at least not correct)
Regards,
Peter
if you use °C as unit for the temperature difference, than SMath calculates intenal with unit K.
This is correct.
Because of the definition: 0°C=273.15K a DeltaT of 5°C would be a diff. of 278,15K !
If MathCAD accepts temp. diffs. with unit °C, than that is im my opinion an error (at least not correct)
Regards,
Peter
#5 Опубликовано: 14.09.2012 05:10:38
Hello Ioan,
if you use °C as unit for the temperature difference, than SMath calculates intenal with unit K.
This is correct.
Because of the definition: 0°C=273.15K a DeltaT of 5°C would be a diff. of 278,15K !
If MathCAD accepts temp. diffs. with unit °C, than that is im my opinion an error (at least not correct)
Regards,
Peter
I agree with you
Note that you can simply use the °C temperature giving as input a temperature difference (as required by the definition of the equation)
regards,
w3b5urf3r
If you like my plugins please consider to support the program buying a license; for personal contributions to me: paypal.me/dcprojects
1 пользователям понравился этот пост
Peter 14.09.2012 05:38:00
#6 Опубликовано: 25.09.2012 18:46:04
This is an issue for me as well. MathCAD has a function called delta T under their units drop down (version 14 at least). Trying to figure out how to write a function that would fix this issue in SMath. I know it took MathCAD a long time to address this issue For me its as simple as 100C - 80C needs to equal 20C and not -253.15C. It appears that they defined DC=K (kelvin) and DF=(5/9)K
Edit 1:
I can confirm. MathCAD does define the deltas as mentioned above. I whole heartedly disagree with Peter and w3b5urf3r. I use the "unit"/scale value of DT ALL the time. An example would be Heat Transfer Coefficients. Take a look at and units on any chart. If you do the math, the "temperature" in the coefficient's units is based on a change (DT). I have gotten into a habit of re-writing these coefficients with a DT such that my calculation output will be a direct unit (be it C or F).
Edit 2: Post from PTC
http://blogs.ptc.com/2012/12/20/the-trickiness-of-temperature-units/
Edit 1:
I can confirm. MathCAD does define the deltas as mentioned above. I whole heartedly disagree with Peter and w3b5urf3r. I use the "unit"/scale value of DT ALL the time. An example would be Heat Transfer Coefficients. Take a look at and units on any chart. If you do the math, the "temperature" in the coefficient's units is based on a change (DT). I have gotten into a habit of re-writing these coefficients with a DT such that my calculation output will be a direct unit (be it C or F).
Edit 2: Post from PTC
http://blogs.ptc.com/2012/12/20/the-trickiness-of-temperature-units/
#7 Опубликовано: 27.01.2013 19:41:25
One more example from the chapter "What you see is not always what you get"
I just played around with temperature units and found an issue that might be a pitfall for the unaware user.
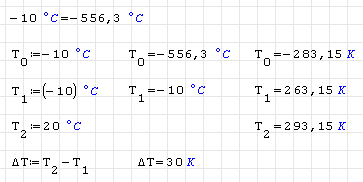
Type the expression -10°C and try to display the value in units °C. You get
-10°C=-556,3°C
On the LHS, times (10 by °C) has higher priority than minus (0 - 10). Thus 10°C is evaluated to 283,15K and then subtracted from zero, giving -283,15K. This is then displayed in °C by subtracting another 273,15 from the value. In the result, everything to the left of the unit is treated as if it was in braces.
The corresponding survival rule is:
"Negative temperature values in non-absolute units (°C, °F, °Re) need to be bracketed"
The other rule is already given in the previous discussion:
"Always display temperature differences in absolute units (K, °Ra)"
I just played around with temperature units and found an issue that might be a pitfall for the unaware user.
Type the expression -10°C and try to display the value in units °C. You get
-10°C=-556,3°C
On the LHS, times (10 by °C) has higher priority than minus (0 - 10). Thus 10°C is evaluated to 283,15K and then subtracted from zero, giving -283,15K. This is then displayed in °C by subtracting another 273,15 from the value. In the result, everything to the left of the unit is treated as if it was in braces.
The corresponding survival rule is:
"Negative temperature values in non-absolute units (°C, °F, °Re) need to be bracketed"
The other rule is already given in the previous discussion:
"Always display temperature differences in absolute units (K, °Ra)"
Martin Kraska
Pre-configured portable distribution of SMath Studio: https://en.smath.info/wiki/SMath%20with%20Plugins.ashx
#8 Опубликовано: 27.01.2013 20:15:57
http://ru.smath.info/forum/yaf_postst1546_Izmienieniie-prioritieta-unarnogho-minusa.aspx
This is not a unit issue, it is a problem with operators priority
This is not a unit issue, it is a problem with operators priority
С уважением,
Михаил Каганский
#9 Опубликовано: 19.10.2016 10:33:31
Sorry to bring up a seemingly old topic with the temperature units but after using the forums Search tool I could not find a satisfying answer.
I do not understand how SMath arrives at the answer shown. I assumed that SMath would have converted to kelvin for the calculations and then converted back to Fahrenheit to display the solution. It does not seem to do that?
Anyways, thanks for entertaining my question.
Temperature Units.sm
I do not understand how SMath arrives at the answer shown. I assumed that SMath would have converted to kelvin for the calculations and then converted back to Fahrenheit to display the solution. It does not seem to do that?
Anyways, thanks for entertaining my question.
Temperature Units.sm
#10 Опубликовано: 19.10.2016 10:47:12
It does convert to Kelvins, then subtracts.
But then you take the temperature difference, and try to show it as temperature. SMath then shows you how much the resulting temperature is higher than zero Farenhait - i.e. how much the 1388.705 K is greater than 255.3722 K.
You should have used units for temperature difference, i.e. 'Δ°F
But then you take the temperature difference, and try to show it as temperature. SMath then shows you how much the resulting temperature is higher than zero Farenhait - i.e. how much the 1388.705 K is greater than 255.3722 K.
You should have used units for temperature difference, i.e. 'Δ°F
С уважением,
Михаил Каганский
#11 Опубликовано: 19.10.2016 11:27:47
mikekaganski,
Thank you for the quick reply. Please forgive me for my elementary understanding of temperature units here. It does not seem logical to me that the units would change during a simple subtraction operation. You explain that I have taken the temperature difference and then ask SMath to show it as temperature. Why would we differentiate the two as different units? Is this a scalar vs vector unit issue?
I understand that the temperature units I am using as inputs are not absolute but it seems like by converting to an absolute scale before the operations and converting back after the operations would result in a correct answer every time.
However, I also understand and appreciate that there could be much more complicated situations the software would have to be prepared for but using a special unit of temperature difference seems silly to me.
Also, please do not take my questions as demeaning. I am not interested in being negative about this wonderful free software. I am however very interested in learning from this community!
Thanks! :d
Thank you for the quick reply. Please forgive me for my elementary understanding of temperature units here. It does not seem logical to me that the units would change during a simple subtraction operation. You explain that I have taken the temperature difference and then ask SMath to show it as temperature. Why would we differentiate the two as different units? Is this a scalar vs vector unit issue?
I understand that the temperature units I am using as inputs are not absolute but it seems like by converting to an absolute scale before the operations and converting back after the operations would result in a correct answer every time.
However, I also understand and appreciate that there could be much more complicated situations the software would have to be prepared for but using a special unit of temperature difference seems silly to me.
Also, please do not take my questions as demeaning. I am not interested in being negative about this wonderful free software. I am however very interested in learning from this community!
Thanks! :d
#12 Опубликовано: 19.10.2016 11:36:50
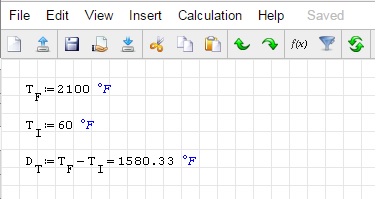
1. T_F := 2100°F = 255.3722 K + (2100*5/9) K = 1422.0389 K
2. T_I := 60°F = 255.3722 K + (60*5/9) K = 288.7056 K
3. T_F - T_I = 1422.0389 K - 288.7056 K = 1133.3333 K
4. 1133.3333 K = (1133.3333 K - 255.3722 K)*9/5 = 1580.33°F
Please note the subtraction in last (fourth) position.
In third position, the two additions are compensated; while the last one has no counterpart.
Temperature in Farenhait is measure how many Farenhait degrees are above zero Farenhait. That's the culpit.
Think about this.
You write: T_I := 60°F + 5°F.
What do you mean? Do you mean that some body has that temperature of 60°F?
And is 5°F the number of degrees that the body got from heating (temperature difference)?
I (human) see your intention. Does the program?
SMath uses base SI units to keep the values. So it will make the following:
60°F + 5°F = 255.3722 K + (60*5/9) K + 255.3722 K + (5*5/9) K = 288.7056 K + 258.15 K = 546.8556 K = 524.67 °F
Addition will make this apparent.
So, you need to use 60°F + 5Δ°F to let program know. And at the same time, to teach yourself discipline in thinking about non-standard temperature scales that have that shifted zero point.
2. T_I := 60°F = 255.3722 K + (60*5/9) K = 288.7056 K
3. T_F - T_I = 1422.0389 K - 288.7056 K = 1133.3333 K
4. 1133.3333 K = (1133.3333 K - 255.3722 K)*9/5 = 1580.33°F
Please note the subtraction in last (fourth) position.
In third position, the two additions are compensated; while the last one has no counterpart.
Temperature in Farenhait is measure how many Farenhait degrees are above zero Farenhait. That's the culpit.
Think about this.
You write: T_I := 60°F + 5°F.
What do you mean? Do you mean that some body has that temperature of 60°F?
And is 5°F the number of degrees that the body got from heating (temperature difference)?
I (human) see your intention. Does the program?
SMath uses base SI units to keep the values. So it will make the following:
60°F + 5°F = 255.3722 K + (60*5/9) K + 255.3722 K + (5*5/9) K = 288.7056 K + 258.15 K = 546.8556 K = 524.67 °F
Addition will make this apparent.
So, you need to use 60°F + 5Δ°F to let program know. And at the same time, to teach yourself discipline in thinking about non-standard temperature scales that have that shifted zero point.
С уважением,
Михаил Каганский
#13 Опубликовано: 19.10.2016 12:10:55
I now understand.
2100-60=2040
1580+460=2040 -->being that Absolute zero is -460 F. and as you said above zero Fahrenheit, Therefore: 0-(-460)=460)
This was not immediately obvious to me.
Thank you for taking the time to explain it to me.
2100-60=2040
1580+460=2040 -->being that Absolute zero is -460 F. and as you said above zero Fahrenheit, Therefore: 0-(-460)=460)
This was not immediately obvious to me.
Thank you for taking the time to explain it to me.
-
Новые сообщения
-
Нет новых сообщений