Вот тут замечательно показан возможный концепт:

[YOUTUBE]http://www.youtube.com/watch?v=uksrGNS0IEA[/YOUTUBE]

Однако подобной реализации "в железе" найти не смог.

UPDATE:

Хотя нет, нашёл-таки!

[YOUTUBE]http://www.youtube.com/watch?v=j5FPhVbA2Hc[/YOUTUBE]

Дык это не сверло, это зенкер или фреза, хотя забавно!

Сверление точного(без закруглений)квадратного отверстия
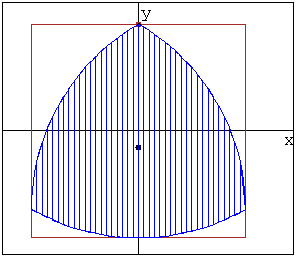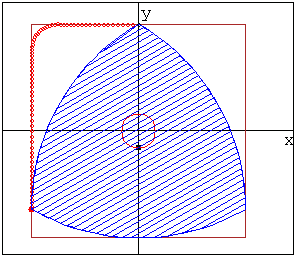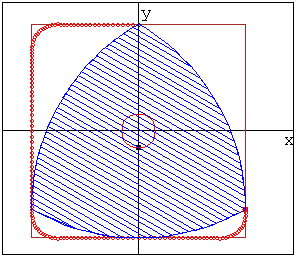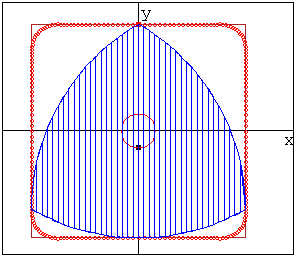
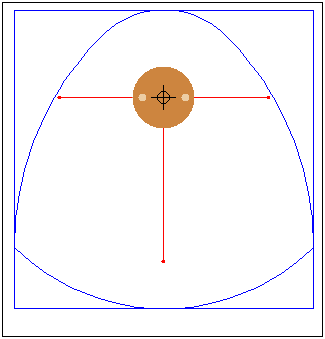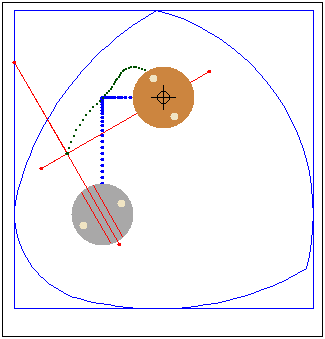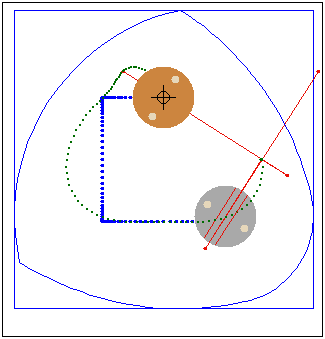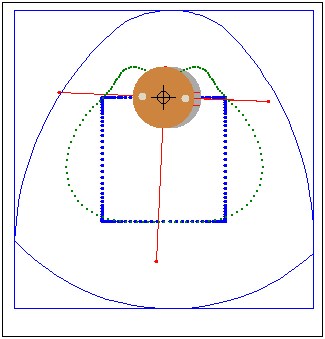
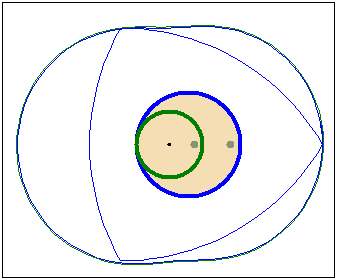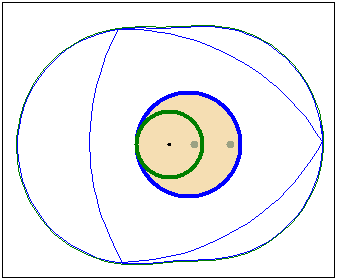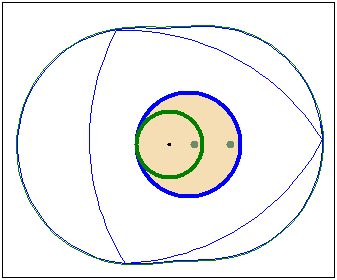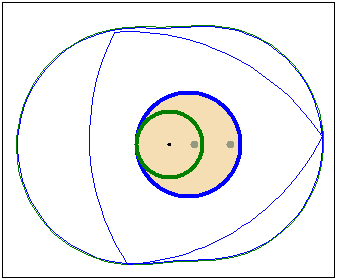
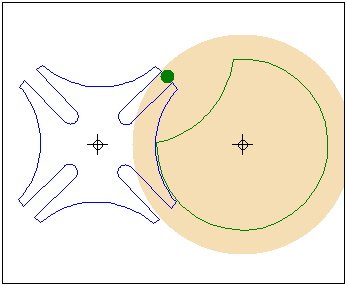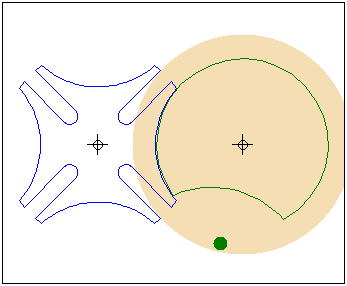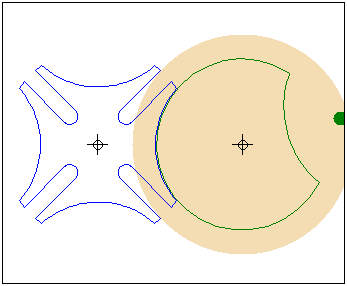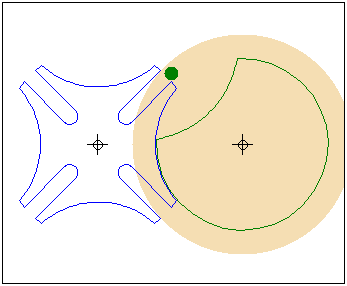
Кулачок в форме модифицированного треугольника Рело
движется в направляющей квадратной рамке.Режущий
инструмент (зеленая точка в центре желтого круга)
прорезает математически точное квадратное отверстие.
Литература:
Wagon S. Mathematica in Action: Problem Solving Through Visualization and Computation,Springer, 2010.

https://smath.com/wiki/GetFile.aspx?File=Drilling2.rar

Wrote

Wrote

Сверление квадратного отверстия сверлом в виде треугольника Рело
Треугольник Рело вращается вокруг своего центра тяжести ,а сам центр тяжести
движется вокруг центра отверстия по траектории,близкой к окружности.

https://smath.com/wiki/GetFile.aspx?File=Reuleauxtriangle.rar

А в реальности такие сверла используются? Или просто как пример дано?

Когда-то давно я работал фрезеровщиком-зуборезчиком. Не знаю как сейчас, но в те времена квадратные полуотверстия (паз для шпонки в шестеренке, например) делали на строгальном (долбежном) станке. И полный квадрат на этом станке можно было сделать - посверлить круглое отверстие и довести его до квадрата на долбежном станке. Квадратные отверстия - это... Им нужны квадратные болты:d Прямоугольные отверстия делают для замков в дверях...Есть спец инструмент для этого. На металле квадратные и прочие сложные отверстия (окно автомобиля) делают, как правило, на листовых заголовках штамповкой.

Wrote

Wrote

Сверление квадратного отверстия сверлом в виде треугольника Рело
Треугольник Рело вращается вокруг своего центра тяжести ,а сам центр тяжести
движется вокруг центра отверстия по траектории,близкой к окружности.

https://smath.com/wiki/GetFile.aspx?File=Reuleauxtriangle.rar

А в реальности такие сверла используются? Или просто как пример дано?

Когда-то давно я работал фрезеровщиком-зуборезщиком. В те времена квадратные (полу) отверстия (например, паз для шпонки в шестеренке) делали на специальном строгальном станке - на долбежном станке. На нем можно было сделать и прямоугольное отверстие из сквозного круглого.

Сверлениe квадратных отверстий (продолжение)
Для сверления квадратных отверстий на обычном сверлильном станке Wagon S.(см.Литература) предлагает использовать крестовую дисковую муфту(муфту Ольдгема).Она состоит из двух полумуфт с пазами на торцевой поверхности и среднего тела-креста, входящего в пазы полумуфт(рисунок).Первая полумуфта соединена с ведущим валом,вторая- соосно со сверлом на диске Рело.При вращении ведущего вала выступы креста скользят по впадинам полумуфт.Крест совершает "плавающее" движение,преобразуя вращательное движение ведущего вала в движение по квадратной траектории.

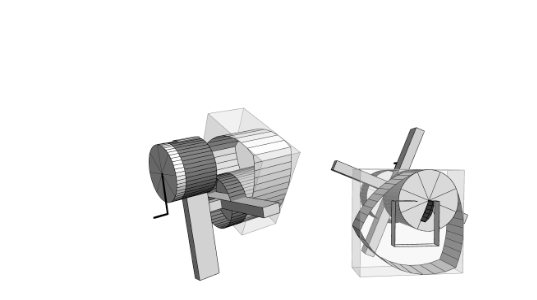
Wrote

Дык это не сверло, это зенкер или фреза, хотя забавно!

Сверло,соединенное с треугольником Рело

Wrote

Wrote

Дык это не сверло, это зенкер или фреза, хотя забавно!

Сверло,соединенное с треугольником Рело

Позвольте спросить, а как этим сверлом сверлить отверстие ?
У сверла ось симметрии, вокруг которого вращаются режущие кромки в центре...
А тут инструмент имеет сложное вращательное движение, да и режущие кромки у него будут не тривиальные, ведь нужно отверстие просверлить, а не рассверливать...

Может быть возможен совмещенный инструмент, сверло, потом зенкер, но это отдельная песня, это дорого, да и затачивать его не удобно...

С уважением!

Двигатель Ванкеля(Ротор-треугольник Рело)

---

Wankel.rar (2 КиБ) скачан 76 раз(а).

Очередная иллюстрация применения метода Драгилева к анимации (вернее, точнейшему расчёту траекторий всех точек) механизма.
http://forum.exponenta.ru/viewtopic.php?p=55657#55657

Плоский трехзвенный манипулятор

---

3R.rar (60 КиБ) скачан 85 раз(а).

Мальтийский механизм

---

Geneva.smz (40 КиБ) скачан 79 раз(а).

Wrote

Мальтийский механизм

Мальтийский крест - это из той же оперы?

Русское «мальтийский механизм» — от внешнего сходства ведомого звена устройства с мальтийским крестом(Материал из Википедии)

Wrote

Русское «мальтийский механизм» — от внешнего сходства ведомого звена устройства с мальтийским крестом(Материал из Википедии)

У вас реализован поворот ведомого вала на 90 градусов. Насколько я понимаю, можно сделать механизм, который будет обеспечивать угол поворота 60, 45 и т.д. градусов?

Анимация кинематических характеристик
Вверху:траектория точки В,векторы ее скорости и ускорения; Внизу:зависимость величин скорости и ускорения точки В от угла поворота кривошипа β(t)

---

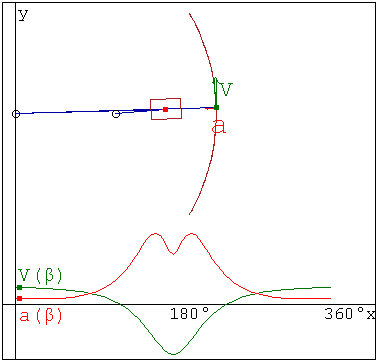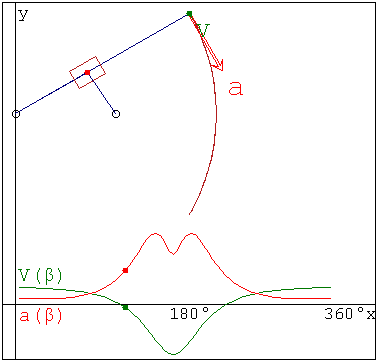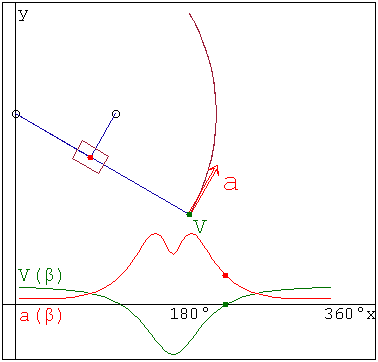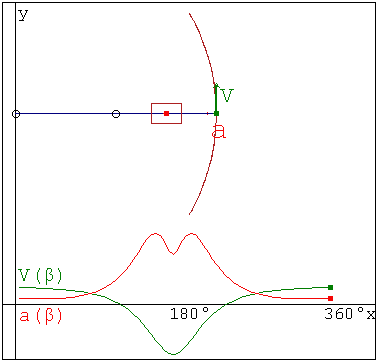
kinchar.smz (11 КиБ) скачан 100 раз(а).

Навеяно сферическим механизмом (шарнир Гука) из книги И.И. Артоболевского “Теория механизмов и машин”. Сфера заменена своим аналогом с 4-ми степенями. Расстояния между точками и принадлежность точек поверхности описываются системой алгебраических уравнений:

C1 := -.84090; C2 := .84090; C3 := 0.;
g1 := 1.; g2 := 0.; g3 := 0.;
L1 := 1.; L2 := 2^.5;
x4^4+x5^4+x6^4-L1^4=0;
x1^4+x2^4+x3^4-L1^4=0;
(g1-x1)^2+(g2-x2)^2+(g3-x3)^2-L2^2=0;
(C1-x4)^2+(C2-x5)^2+(C3-x6)^2-L2^2=0;
(x1-x4)^2+(x2-x5)^2+(x3-x6)^2-L2^2=0;

На рисунке показаны поверхность, стационарные точки, траектории точек на поверхности, отрезки, соединяющие точки, и ещё вспомогательные плоскости в виде треугольников с перпендикулярами к ним для улучшения визуальной передачи особенностей движения. Выполнено в пакете Maple.

Анимация пространственных механизмов
Для расчета положений механизмов будем использовать
методы,разработанные А.Б.Ивановым.Свои работы по 3d
анимации механизмов ,выполненные в Mapl, А.Б.Иванов публикует
на сайте
http://forum.exponenta.ru/viewtopic.php?t=12842
Часть примеров с этого сайта я перенес в среду программирования SMath Studio.
1.Механизм Саррюса 1( Sarrus linkage 1)

Анимация пространственных механизмов
Для расчета положений механизмов будем использовать
методы,разработанные А.Б.Ивановым.Свои работы по 3d
анимации механизмов ,выполненные в Mapl, А.Б.Иванов публикует
на сайте
http://forum.exponenta.ru/viewtopic.php?t=12842
Часть примеров с этого сайта я перенес в среду программирования SMath Studio.
1.Механизм Саррюса 1( Sarrus linkage 1)