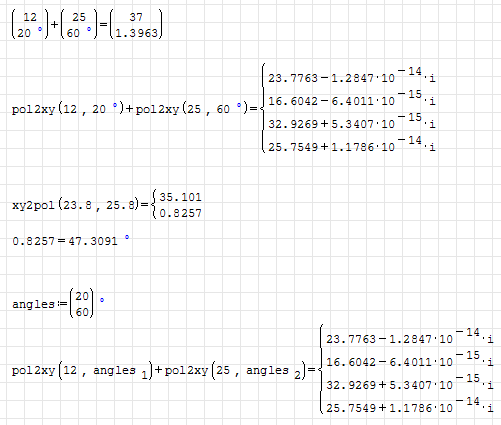Vector Addition (scalar, direction) with vector result - How to add vectors (scalar, direction) and get a vector result - Сообщения
#1 Опубликовано: 19.09.2013 13:54:12
Hello all
I have two vectors with scalar and direction that I want to add and get a resulting vector that has scalar and direction. I can't seem to figure this out? Basically I have a force problem that I am solving for and I figured this would be best done by adding the vectors to get the resulting force however I can't seem to figure this out on SMath.
Thank-you to all who answer.
I have two vectors with scalar and direction that I want to add and get a resulting vector that has scalar and direction. I can't seem to figure this out? Basically I have a force problem that I am solving for and I figured this would be best done by adding the vectors to get the resulting force however I can't seem to figure this out on SMath.
Thank-you to all who answer.
#2 Опубликовано: 20.09.2013 12:11:07
Can you post an example (from literature or made by you)?
If you like my plugins please consider to support the program buying a license; for personal contributions to me: paypal.me/dcprojects
#3 Опубликовано: 20.09.2013 17:14:59
oops I never tried this, I think he means this
http://www.1728.org/vectors.htm
I might be wrong but SMath does not calculate sum of vectors given in polar coordinates correctly
http://www.1728.org/vectors.htm
I might be wrong but SMath does not calculate sum of vectors given in polar coordinates correctly
1 пользователям понравился этот пост
Davide Carpi 20.09.2013 17:57:00
#4 Опубликовано: 20.09.2013 18:03:54
Actually, there are several ways to calculate vector sums. In 2D the most natural way for vectors given in polar form is using complex numbers. In mechanics, we usually transform to cartesian components, as this can be generalized to 3D.
Unfortunately, this example reveals that the handling of sums in Maxima plugin is very weak at the moment. Therefore, we have to "surrender" for the moment.
Example adding 2D vectors.sm
Unfortunately, this example reveals that the handling of sums in Maxima plugin is very weak at the moment. Therefore, we have to "surrender" for the moment.
Example adding 2D vectors.sm
Martin Kraska
Pre-configured portable distribution of SMath Studio: https://en.smath.info/wiki/SMath%20with%20Plugins.ashx
#5 Опубликовано: 20.09.2013 18:06:30
oops I never tried this, I think he means this
http://www.1728.org/vectors.htm
I might be wrong but SMath does not calculate sum of vectors given in polar coordinates correctly
I think you are right; BTW is a quite simple problem, so one can build his own function, with the most appropriate input standard that he think better and, like has Martin said, there are several ways to process the problem
If you like my plugins please consider to support the program buying a license; for personal contributions to me: paypal.me/dcprojects
#6 Опубликовано: 21.09.2013 06:58:41
I think the question is about adding vectors entered in polar form as in the first expression. Note that SMath does not return the correct result.
#7 Опубликовано: 21.09.2013 08:10:45
Note that SMath does not return the correct result.
Lists and list operations are not a good representation for vectors and vector operations. If lists obtained by pol2xy are to be added, they must be converted to vectors using sys2mat().
Martin Kraska
Pre-configured portable distribution of SMath Studio: https://en.smath.info/wiki/SMath%20with%20Plugins.ashx
#8 Опубликовано: 21.09.2013 08:38:27
@ioan92
Nice explanation on how to get a result. The point of the original question, I think, was a direct way using only polar notation provided by SMath
@mkraska
I forgot to apply sys2mat to an expression involving more than one system, anyway the result of that sum is incorrect.
Nice explanation on how to get a result. The point of the original question, I think, was a direct way using only polar notation provided by SMath
@mkraska
I forgot to apply sys2mat to an expression involving more than one system, anyway the result of that sum is incorrect.
1 пользователям понравился этот пост
ioan92 21.09.2013 08:57:00
-
Новые сообщения
-
Нет новых сообщений