I have an equation that is dependent on the summation of terms and I need to integrate that equation. I can do it if i evaluate the summations myself but I am going to need many terms and was wondering if there is a way to do this without having to evaluate it myself?

I have attached a file of the equation I am trying to integrate.intsum.sm (12 КиБ) скачан 40 раз(а).

Hi Camdem. Use line(...) for prevent the evaluation in Phi.series function. Then, integral could be evaluated.

intsum.sm (12 КиБ) скачан 45 раз(а).



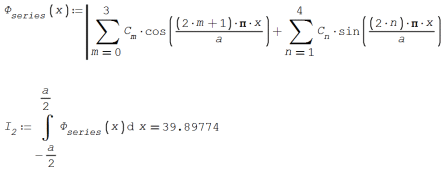
Best regards.
Alvaro.

Thank you very much Alvaro

Wrote

I have an equation that is dependent on the summation of terms

Just a comment: the creation of the signal is so involved
that makes me doubt it come from Scientifics [just personal].
If it comes from a data set, tentatively approximated, it may
have much simpler representation.
I can look at it if interested, just the data set.

Cheers ... Jean

Wrote

If it comes from a data set, tentatively approximated, it may
have much simpler representation.
I

... would be much better from original data set.
If not appreciated: will delete all my replies.

Jean,

I appreciate what you have said and done so far. Unfortunately, though, the equation is from a series approximation of the equation I have attached. It doesn't come from a data set.

This attached equation is a solution to the diffusion equation with a non-uniform source.

Wrote

This attached equation is a solution to the diffusion equation with a non-uniform source.

... NO attachment !

Jean,

The attachment I was referencing was the picture of the equation.

analytic.sm (2 КиБ) скачан 36 раз(а). Here is the equation in smath.

Sorry about the confusion.

Wrote

the equation is from a series approximation

... you mean S(x) approximates experimental data collection.
Why not integrate Φ.analytic(x) ?
There may be much suitable model than series approximation.
Quite a few Scientific works have never been done yet except in Smath:
Kirby, Han, Turber, Ant Colony, Termocouples [T,J]
RTD, Germanium -273.15, Copper in high magnetic induction ...

I have 100's model functions [addicted for more than 50 years].
Often, just look at raw data ... got the model or best fit.
Best success ... don't hesitate for + + +
Watch what you borrow from Others, I mean S(x).

Cheers ... Jean.

Jean,

S(x) is the function that the source follows, it defines the value of the source at each point along the distance in the medium and is given for the medium.

On the grounds of integrating the analytic(x), I actually am elsewhere. I am comparing the series solution to the analytic solution to show that the series solution is a good model once enough summation terms are added. In some cases, the diffusion equation will not have an analytic solution and the series solution is necessary to model the system. therefore, I need to show that the series solution is valid.

In terms of other models, I have been instructed to use the series solution that I have.

Sincerely,
Cam

Wrote

Jean,

S(x) is the function that the source follows, it defines the value of the source at each point along the distance in the medium and is given for the medium.

On the grounds of integrating the analytic(x), I actually am elsewhere. I am comparing the series solution to the analytic solution to show that the series solution is a good model once enough summation terms are added.In some cases, the diffusion equation will not have an analytic solution and the series solution is necessary to model the system.therefore, I need to show that the series solution is valid.

In terms of other models,I have been instructed to use the series solution that I have.

Sincerely,
Cam

Thanks Cam, you express yourself very well.
I retain that on some experiment S(x) is not profitable,
then in lieu you propose the trig summation ... Ah !
Therefore: you construct accordingly to what S(x) fails.
At this point, and assuming that the "Camel shape" does not
do too much "monkey branching", linfitCheby is a much better
candidate as you just need to set the ChebyShev oder.
The final export is a gracious function ready for scientific calculator.
"linfitCheby" resulted for the extension of the Mathcad built-in 'linfit'.
More can be done as we can mask some components.
Two more candidates are valid: OVNI model, Fourier Budapest 39
More data sets are needed to examine their applicability.

Cheers Cam ... Jean

Genfit linfitCheby.sm (77 КиБ) скачан 35 раз(а).

Jean,

Thank you very much for pointing out those other candidates. I appreciate all that you have said.

Sincerely,
Cam