1 страниц (5 вхождений)
Ошибка при вычислении интеграла - Сообщения
#1 Опубликовано: 12.10.2009 12:44:49
Не вычисляется интеграл вот такой функции
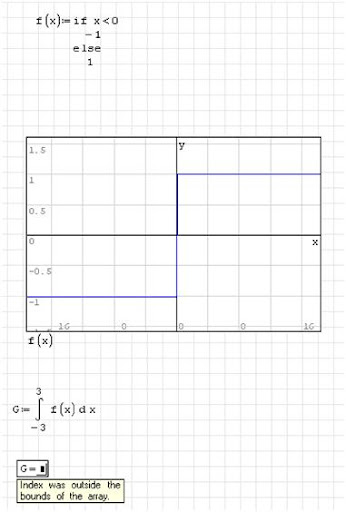
Т.е. не только эта конкретная функция, а вообще любая кусочно-гладкая функция, даже непрерывная)
Опять же это вещь нужная для практической работы.
Т.е. не только эта конкретная функция, а вообще любая кусочно-гладкая функция, даже непрерывная)
Опять же это вещь нужная для практической работы.
#2 Опубликовано: 12.10.2009 14:35:40
Да, проблема известная. Дело в том, что функцию if нельзя использовать в подынтегральном выражении. Постараюсь подумать, как это можно обойти, но задача эта нетривиальна т.к. вычислением интегралов занимается простой численный метод Симпсона.
#3 Опубликовано: 12.10.2009 19:42:09
Задача может и не простая, но ответ не принимается)))
Функция: [math]f(x)←sign(sin(x*180/π))[/math] вычисляется, хотя тогда тоже не должна бы, а вот при помощи "примеров" можно вычислить интеграл по методу Симпсона даже для функций с if. Правда вычисляется довольно грубо, даже при точности 100, а вот при 1000 вычисления не завершились и за 2 минуты.(((
На самом деле это все не страшно, если будет реализовано, как обещано, легко доступное плагинописание на C#, тогда лично для меня отпадут такие вопросы. Ну и конечно это плагинописание желательно должно быть встроено в систему, совместно с компилятором и отладчиком(ну это в идеале). Ждем)))
Функция: [math]f(x)←sign(sin(x*180/π))[/math] вычисляется, хотя тогда тоже не должна бы, а вот при помощи "примеров" можно вычислить интеграл по методу Симпсона даже для функций с if. Правда вычисляется довольно грубо, даже при точности 100, а вот при 1000 вычисления не завершились и за 2 минуты.(((
На самом деле это все не страшно, если будет реализовано, как обещано, легко доступное плагинописание на C#, тогда лично для меня отпадут такие вопросы. Ну и конечно это плагинописание желательно должно быть встроено в систему, совместно с компилятором и отладчиком(ну это в идеале). Ждем)))
#4 Опубликовано: 10.05.2010 11:15:34
Здравствуйте. Воть обнаружил что несобственные интеграллы не вычисляются. Если не ошибаюсь то метод симпсона использует интерполяцию квадратным трёхчленом, а в случае отрицательных степеней подобная интерполяция работаит плохо. При увеличении верхней границы интеграла от x^(-3)dx результат неограниченно возрастает. А как считать предел я не нашел.
И вопрос, почему бы при интегрировании просто не использовать метод прямоугольников?
И вопрос, почему бы при интегрировании просто не использовать метод прямоугольников?
#5 Опубликовано: 10.05.2010 20:38:27
Wrote
И вопрос, почему бы при интегрировании просто не использовать метод прямоугольников?
Хуже сходимость.
При вычислении несобственного интеграла II рода, можно перейти к несобственному интегралу I рода и применить метод Симпсона
1 страниц (5 вхождений)
- Новые сообщения
- Нет новых сообщений
