Hi everybody!
I'm beginner in Smath. I met a problem when use explicit function. I can't show values of variable in decimal format (in case it's irrational number).
In my example, please tell me How to show value of a in decimal format in expression of c. Thanks

Показать спойлер

Tip for your snippets

1. Download WinGrab [freeware] ... put it in the task bar
2. Click on WinGrab to have it active, click "capture"", click F11
if you have set it active [maybe it's not free on your system,
in that case, code it otherwise]
3. At this point, your entire Smath is in full screen in Wingrab.
4. From WinGrab menu => selection tool
5. Strech up/down ... left/right for the portion of your Smath region
6. Crop image from from WinGrab menu
7. Save as *.PNG in your Snippet file.

So, you will just have the portion of interest.
That avoids over clogging the Smath forum server and ease the visitors.

Wrote

How to show value of a in decimal format in expression of c

Maybe just click right for the "Numeric option"
If you define a:=1, b:=2, c:=3, d:=pi

MyStuff:=a*b*c*d ... what is the point to display
MysStuff=1*2*3*3.14159=

Wrote

Tip for your snippets

1. Download WinGrab [freeware] ... put it in the task bar
2. Click on WinGrab to have it active, click "capture"", click F11
if you have set it active [maybe it's not free on your system,
in that case, code it otherwise]
3. At this point, your entire Smath is in full screen in Wingrab.
4. From WinGrab menu => selection tool
5. Strech up/down ... left/right for the portion of your Smath region
6. Crop image from from WinGrab menu
7. Save as *.PNG in your Snippet file.

So, you will just have the portion of interest.
That avoids over clogging the Smath forum server and ease the visitors.

I'm so sorry, I forgot crop image

Ever heard of the windows snipping tool? It is already on board, no need to install anything.
Just type "sni" in the search field of the start menu.

If mouse cursor, callouts and the like are of importance, I use Greenshot.

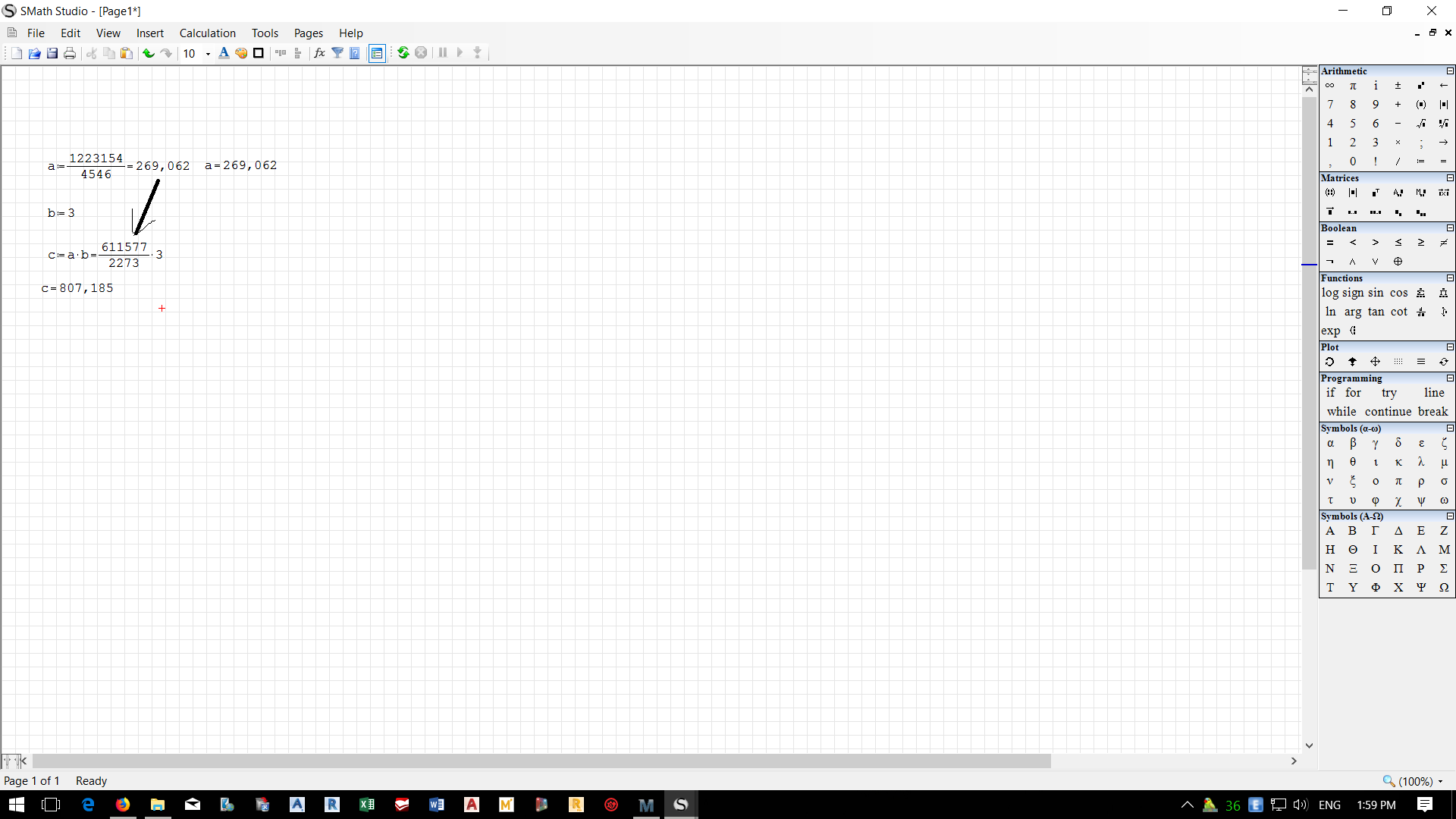
Wrote

Wrote

How to show value of a in decimal format in expression of c

Maybe just click right for the "Numeric option"
If you define a:=1, b:=2, c:=3, d:=pi

MyStuff:=a*b*c*d ... what is the point to display
MysStuff=1*2*3*3.14159=

I followed your instructions. But the problem remains unresolved. Do you have any other way?

Wrote

I followed your instructions. But the problem remains unresolved. Do you have any other way?

A Snippet + Work sheet to check consistency in you PC.
To get all the trailing 0' => set decimals 15 [first]
then set "Trailing 0's => 15.
If you visit Abramowitz & Stegun, you will find lot of
approximations are in fixed arithmetic rational fractions.

Does it help ?

Hanoi.sm (23 КиБ) скачан 46 раз(а).

Very helpful, thank you very much!

Wrote

Very helpful, thank you very much!

Welcome ... read more of interest. So savant a computer may be,
NONE contains mathematical functions, only the 4 arithmetic
operations [+,-,*,/] ... logic, memory as well.
Common functions: Exp(x), ln(x), X^Y [Power function], trig, SQRT...
come with Windows. More advanced functions [Si, Ei, Bessel ...]
are implemented by the software you use [Mathematica, Maple, ...]
In PC's, common functions are approximated from normalised
rational fractions giving 18/21 decimals, from which only 15 are
conserved and displayed. Main frames have supplementary base accuracy
from Chebyshev 25 decimals very stable.

As far as now, Smath will not display > 15 decimals [like Excel...].
Mathcad, Maple, Mathematica ... run what they call "Big Engine"
that will deploy all the floating point register. At the beginning
of the "Main Frames" approximation of functions were done from
Continued Fractions, slow but infinitely unlimited. Thus, Mathcad
could output 250/400 decimals for sin(something), SQRT(2) ... etc.

References:

1. C.T. Fike [Continued Fractions]
2. Luke, Clenshaw [Chebysev]
3. Cody junior [general implementation of rational fractions]
4. Hart et Al. [all collected rational fractions]

Have a good day and enjoy Smath ... Jean

Ah ! here is one that freaks the rules, from "while loop".

Page6 chirpLSQ Supsmooth.sm (105 КиБ) скачан 40 раз(а).

Thank you Jean for your excellent example of using the function "While - loop".

But what happends if the data is not in order?

I think that before the function "While - loop", you must add a routine to sort the data ascending, and thus be sure that the data will be processed correctly, if not sorted.

Best regards.

Carlos

Explicit ... that's a big word.
Follow this document but don't drop dead seeing rational expressions 3 pages wide.
We talked about Continued Fraction, here is an example in applied Engineering.
Many, very many physical phenomenons are of rational form thus of Continued fraction form.
Continued fractions are calculated bottom up [for instance Excel that is brute force].
Smath does it nicely behind the scene. In fact, by itself it reconstructs a Num/Den rational polynomial.

Maple has conserved the conversion from Continued fraction to J_Fraction [explained in C.T. Fike].
Called an economized conversion. This document is complete by itself. The point of interest is wrt
the immensely long explicit, easy to manipulate to produce an elegant formulation.

The Mathcad 11 and earlier is easier to manipulate, it accesses Maple float

This document is Smath 6179 ... may just be different than more recent version.

Thiele Procedure QUICK Simplify_Collect.sm (54 КиБ) скачан 64 раз(а).