1 страниц (3 вхождений)
Using vectors for storing recursive calculation data - Сообщения
Hello!
Is it possible to speed up recursive calculations by using vectors to store previous data? Right now I have a function that calculates a value for each step and uses the result of the previous step to calculate the next one. Sadly the functions becomes very slow when the step starts reaching around 20, as it calculates all of the previous steps as well. Also the limit is 50 steps as far as I know.
For example lets say I have a vector x with a range of 1...10. For a new vector y I would like to take the value from x and add the previous value from x to it (except for the first one, as it does not have a previous value). So the new vector y would be 1, 2+1, 3+2, 4+3 and so on.
Any help on how to do something like this would be very much appreciated.
Is it possible to speed up recursive calculations by using vectors to store previous data? Right now I have a function that calculates a value for each step and uses the result of the previous step to calculate the next one. Sadly the functions becomes very slow when the step starts reaching around 20, as it calculates all of the previous steps as well. Also the limit is 50 steps as far as I know.
For example lets say I have a vector x with a range of 1...10. For a new vector y I would like to take the value from x and add the previous value from x to it (except for the first one, as it does not have a previous value). So the new vector y would be 1, 2+1, 3+2, 4+3 and so on.
Any help on how to do something like this would be very much appreciated.
Try to see if this Razonar solution solves your problem
https://en.smath.com/forum/yaf_postsm71323_Recursion.aspx#post71323
sergio
https://en.smath.com/forum/yaf_postsm71323_Recursion.aspx#post71323
sergio
Greetings,
I am also interested in speeding up recursive calculations. Unfortanelty, I haven't had much time to explore optimization.
You could use a plugin; plugins can perform those recursive iterations outside of the SMath Worksheet environment, thus speeding up your runtime.
Another thought would be to use the recursive features already pre-programmed into SMath (e.g., use of Factorial, Summation, Integral) instead of utilizing the 'programming' functions of for/while.
For example, I used the summation to modify the elements of variable 'y' to reference the previous variables of 'y' and thus created a Fibonacci Sequence in fractions of a second:
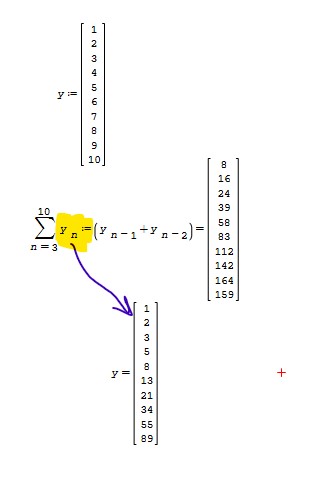
Hope this is of help,
-Kenny Lemens, P.E. ᵂᴵ
I am also interested in speeding up recursive calculations. Unfortanelty, I haven't had much time to explore optimization.
You could use a plugin; plugins can perform those recursive iterations outside of the SMath Worksheet environment, thus speeding up your runtime.
Another thought would be to use the recursive features already pre-programmed into SMath (e.g., use of Factorial, Summation, Integral) instead of utilizing the 'programming' functions of for/while.
For example, I used the summation to modify the elements of variable 'y' to reference the previous variables of 'y' and thus created a Fibonacci Sequence in fractions of a second:

Hope this is of help,
-Kenny Lemens, P.E. ᵂᴵ
"No matter where you go, there you are." -Buckaroo BanzaiHotkeys: https://en.smath.com/forum/resource.ashx?a=45771&b=2
1 страниц (3 вхождений)
- Новые сообщения
- Нет новых сообщений
