1 страниц (5 вхождений)
Дополнение DotNumerics - Набор функций для численного решения ОДУ и систем линейных уравнений. - Сообщения
#1 Опубликовано: 24.07.2013 03:06:00
Состав:
dn_AdamsMoulton(), dn_ExplicitRK45(), dn_ImplicitRK5(), dn_GearsBDF(),
dn_LinAlgSolve(), dn_LinAlgLLS_COF(), dn_LinAlgLLS_QRorLQ(), dn_LinAlgLLS_SVD(), dn_LinAlgSVD(), dn_LinAlgEigenvalues(), dn_LinAlgEigenvectors(), dn_MatrixInverse().
Дифференциальные уравнения. Функции предназначены для численного решения дифференциальных уравнений различными методами: явный Рунге-Кутта, неявный Рунге-Кутта, Gear’s BDF и Адамса-Мултона.
Решатели нежёстких ОДУ:
dn_AdamsMoulton( НачУсл, НачИнт, КонИнт, КолвоИнт, D(2) ) численно решает нежёсткое ОДУ методом Адамса-Мултона.
dn_ExplicitRK45( НачУсл, НачИнт, КонИнт, КолвоИнт, D(2) ) численно решает нежёсткое ОДУ явным методом Рунге-Кутта (4)5 порядка.
Решатели жёстких ОДУ:
dn_ImplicitRK5( НачУсл, НачИнт, КонИнт, КолвоИнт, D(2) ) численно решает жёсткое ОДУ неявным методом Рунге-Кутта 5-го порядка.
dn_GearsBDF( НачУсл, НачИнт, КонИнт, КолвоИнт, D(2) ) численно решает жёсткое ОДУ BDF методом.
Параметры:
НачУсл - вектор начальных условий размерности n, где n - число уравнений в системе;
НачИнт, КонИнт - граничные точки отрезка, на котором ищется решение; начальные условия, заданные в векторе НачУсл, - это значения решения в точке НачИнт;
КолвоИнт - количество интервалов разбиения отрезка [НачИнт, КонИнт], при этом количество точек решения будет равно КолвоИнт + 1;
D(2) - функция двух переменных, возвращающая значение в виде вектора из n элементов, содержащих первые производные неизвестных функций.
Точность
Для всех методов может быть задана прямо в документе перед использованием функции. Для этого нужно определить значения переменных: AbsTol и RelTol. Значения по умолчанию для всех методов: AbsTol = 1.0E-7, RelTol = 1.0E-4.
Примечание. Количество параметров функции D(t,x) может быть больше двух. Вы можете передавать дополнительно какие-то свои параметры как в виде скаляров, так и в виде вектора.
Исходный код: https://smath.info/svn/public/plugins/DotNumerics/
Книги:
1. Numerical initial value problems in ordinary differential equations, C. William Gear, PH, 1971, ISBN 0136266061 (BookFinder).
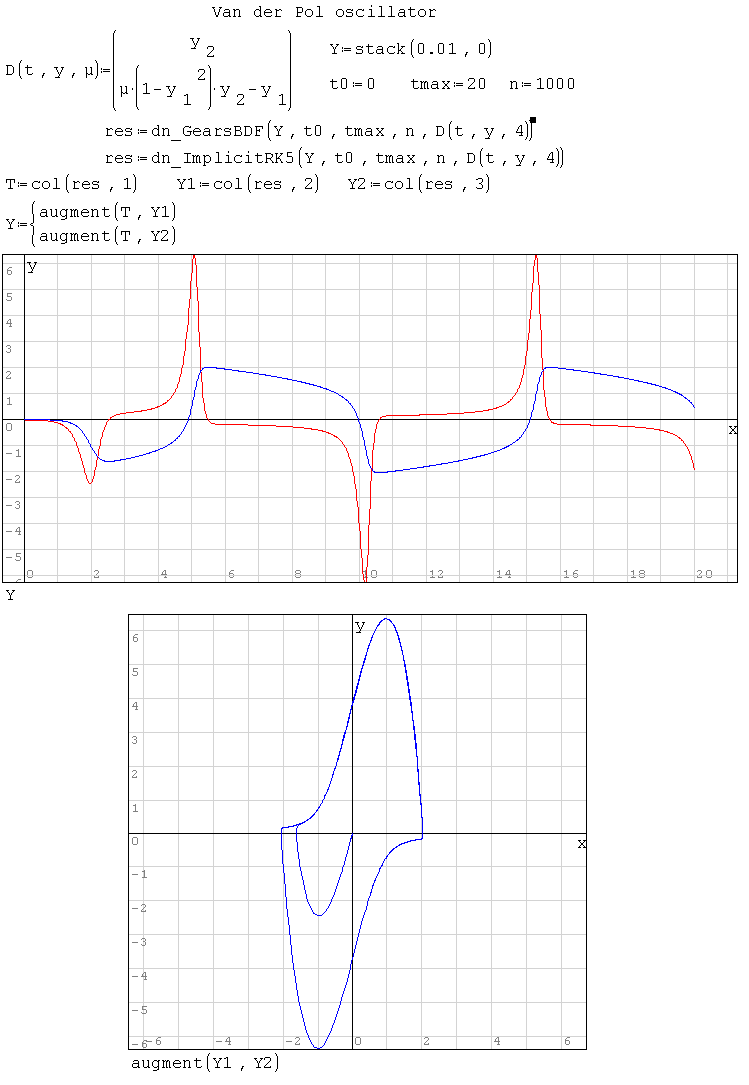
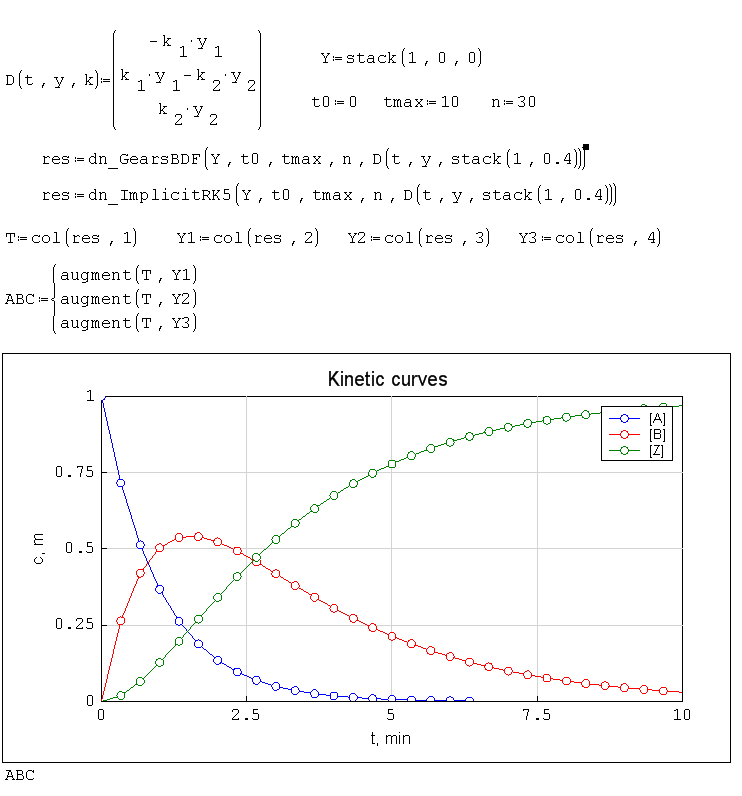
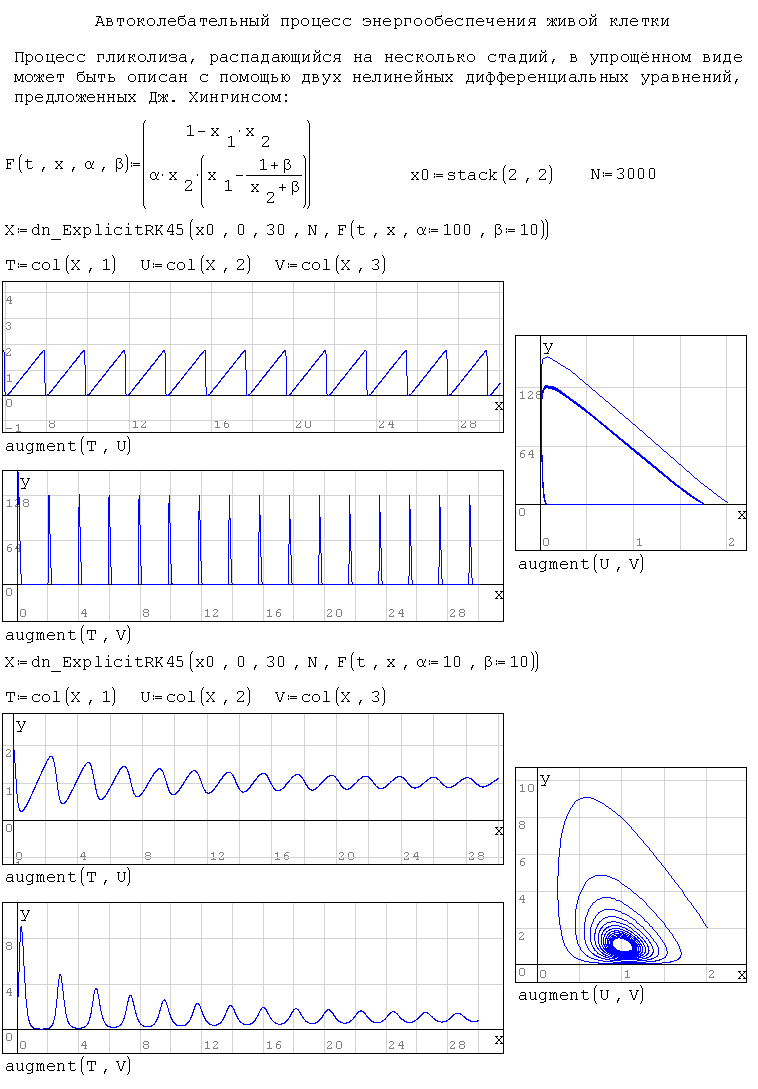
Примеры:
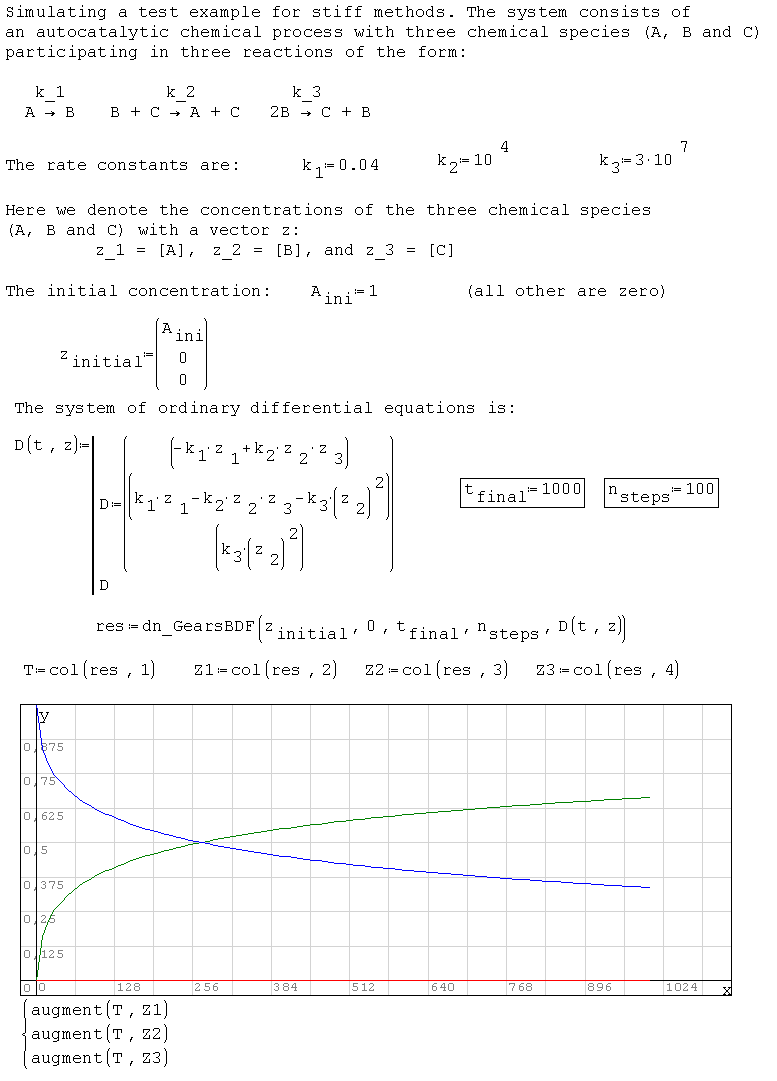
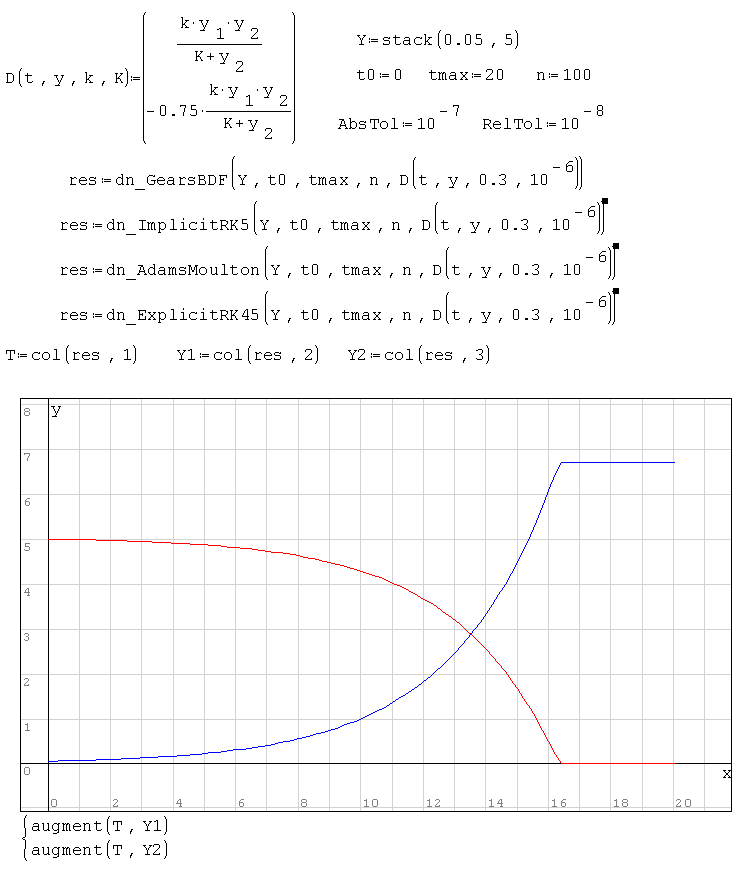


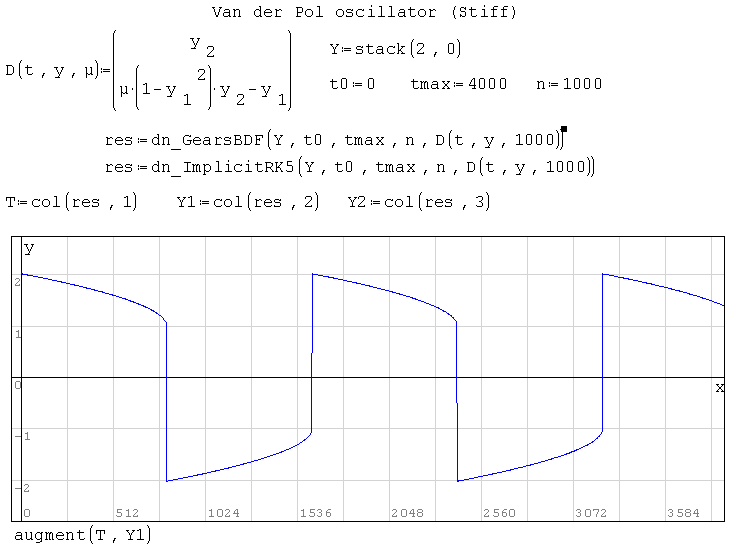
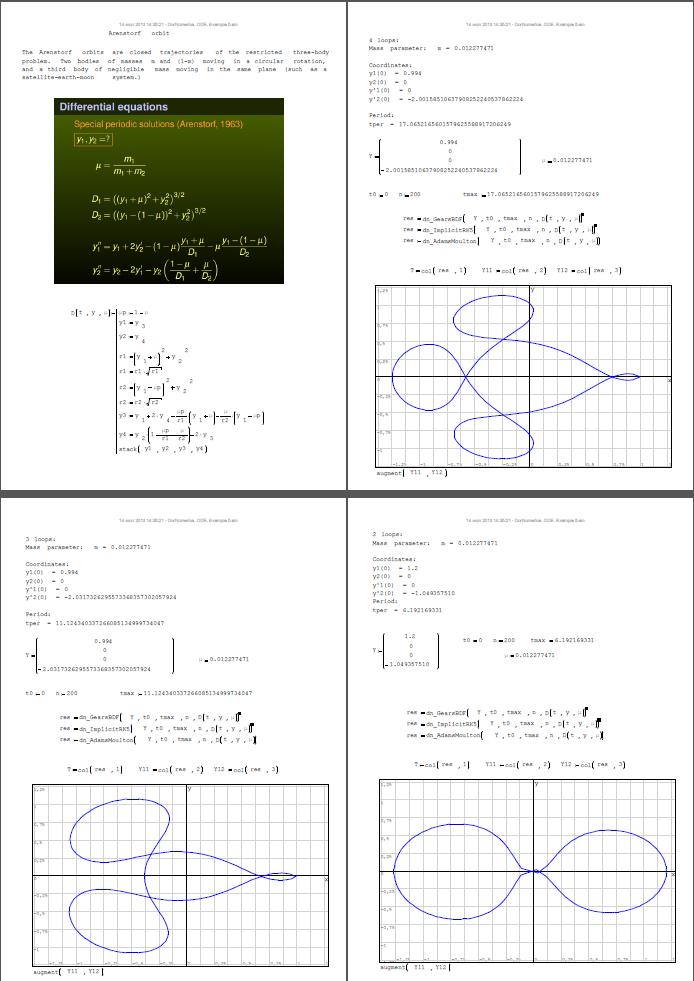
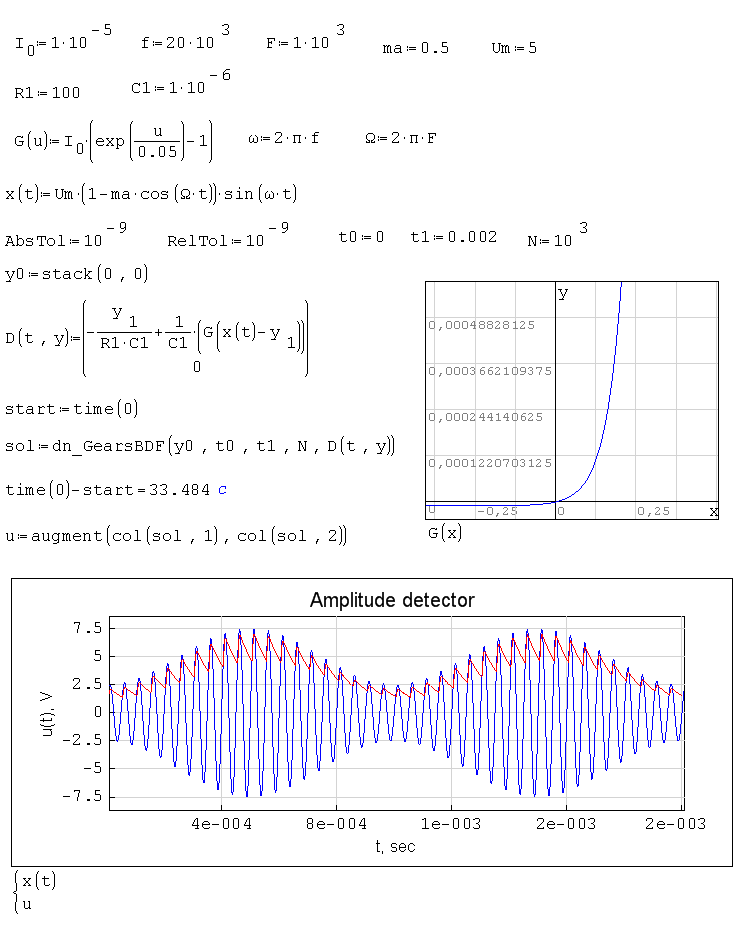
dn_AdamsMoulton(), dn_ExplicitRK45(), dn_ImplicitRK5(), dn_GearsBDF(),
dn_LinAlgSolve(), dn_LinAlgLLS_COF(), dn_LinAlgLLS_QRorLQ(), dn_LinAlgLLS_SVD(), dn_LinAlgSVD(), dn_LinAlgEigenvalues(), dn_LinAlgEigenvectors(), dn_MatrixInverse().
Дифференциальные уравнения. Функции предназначены для численного решения дифференциальных уравнений различными методами: явный Рунге-Кутта, неявный Рунге-Кутта, Gear’s BDF и Адамса-Мултона.
Решатели нежёстких ОДУ:
dn_AdamsMoulton( НачУсл, НачИнт, КонИнт, КолвоИнт, D(2) ) численно решает нежёсткое ОДУ методом Адамса-Мултона.
dn_ExplicitRK45( НачУсл, НачИнт, КонИнт, КолвоИнт, D(2) ) численно решает нежёсткое ОДУ явным методом Рунге-Кутта (4)5 порядка.
Решатели жёстких ОДУ:
dn_ImplicitRK5( НачУсл, НачИнт, КонИнт, КолвоИнт, D(2) ) численно решает жёсткое ОДУ неявным методом Рунге-Кутта 5-го порядка.
dn_GearsBDF( НачУсл, НачИнт, КонИнт, КолвоИнт, D(2) ) численно решает жёсткое ОДУ BDF методом.
Параметры:
НачУсл - вектор начальных условий размерности n, где n - число уравнений в системе;
НачИнт, КонИнт - граничные точки отрезка, на котором ищется решение; начальные условия, заданные в векторе НачУсл, - это значения решения в точке НачИнт;
КолвоИнт - количество интервалов разбиения отрезка [НачИнт, КонИнт], при этом количество точек решения будет равно КолвоИнт + 1;
D(2) - функция двух переменных, возвращающая значение в виде вектора из n элементов, содержащих первые производные неизвестных функций.
Точность
Для всех методов может быть задана прямо в документе перед использованием функции. Для этого нужно определить значения переменных: AbsTol и RelTol. Значения по умолчанию для всех методов: AbsTol = 1.0E-7, RelTol = 1.0E-4.
Примечание. Количество параметров функции D(t,x) может быть больше двух. Вы можете передавать дополнительно какие-то свои параметры как в виде скаляров, так и в виде вектора.



Исходный код: https://smath.info/svn/public/plugins/DotNumerics/
Книги:
1. Numerical initial value problems in ordinary differential equations, C. William Gear, PH, 1971, ISBN 0136266061 (BookFinder).
Примеры:






Россия навсегда!
Вячеслав Мезенцев
1 пользователям понравился этот пост
Serg 25.01.2014 13:44:00
#2 Опубликовано: 25.07.2013 02:54:00
И как это все прикрутить к SMath? Какую .dll куда копировать?
#3 Опубликовано: 25.07.2013 03:30:35
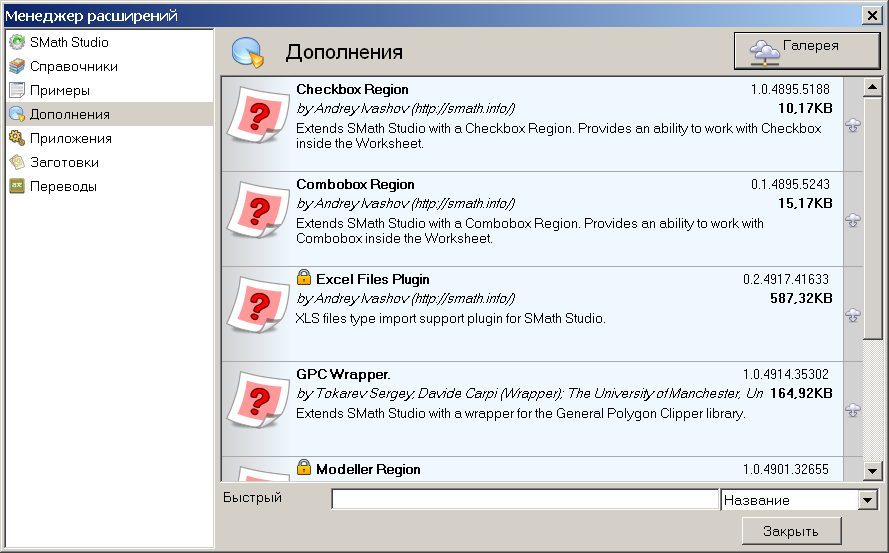
Андрей не афиширует это на местном форуме, но в последней сборке изменён подход к установке дополнений. Там появился специальный менеджер расширений.
Россия навсегда!
Вячеслав Мезенцев
#4 Опубликовано: 26.07.2013 07:07:59
WroteАндрей не афиширует это на местном форуме, но в последней сборке изменён подход к установке дополнений. Там появился специальный менеджер расширений.
Дискриминация по "форумному" признаку?
А ночная сборка - это типа нестабильная версия?
#5 Опубликовано: 26.07.2013 08:40:56
Да, не проверенная. Там появились некоторые значительные изменения и исправления из прошлых сборок. Нужно тестировать. Ещё на английской части форума появился специальный раздел для дополнений, где они все собраны. Здесь мало активных пользователей, поэтому там обновления приоритетней. Тамошние форумчане отписываются об ошибках в программе и по мере их исправления Андрей выкладывал ночные сборки.
Россия навсегда!
Вячеслав Мезенцев
1 страниц (5 вхождений)
- Новые сообщения
- Нет новых сообщений
