Intersections Again - Сообщения
#1 Опубликовано: 18.07.2020 09:08:11
Hi All,
Trying to work out a universal way of getting the length of intersecting lines, easy when lines are level, but not so (for me) others.
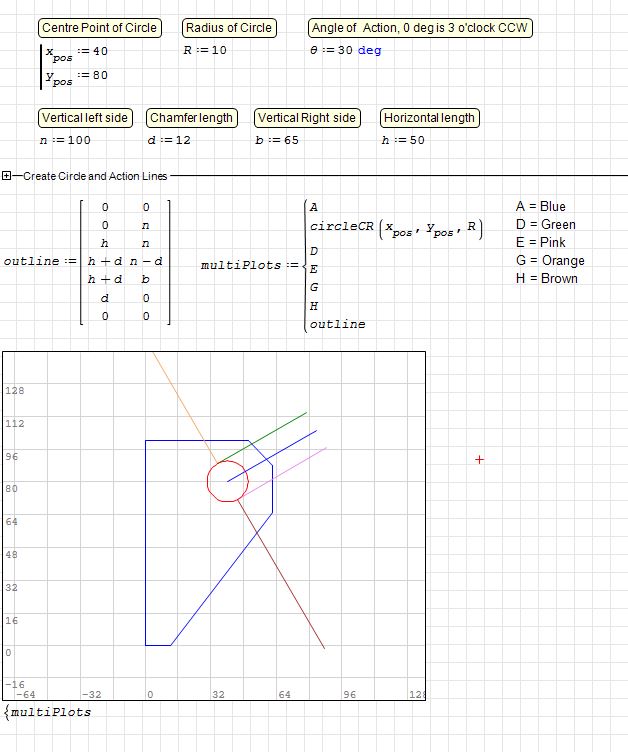
The image below shows a lifting lug, the angle of action can be 0 deg to 150 deg for example. I need to know the length of the lines from the red circle to the outline, individually, then I can see the shortest length, this must be for all angles, effectively tracing the intersection point through the angles. I know I can use Pythagoras, but was hoping to use something like GPC, but this works only for polygons?
Lug Horizontal.sm
Trying to work out a universal way of getting the length of intersecting lines, easy when lines are level, but not so (for me) others.
The image below shows a lifting lug, the angle of action can be 0 deg to 150 deg for example. I need to know the length of the lines from the red circle to the outline, individually, then I can see the shortest length, this must be for all angles, effectively tracing the intersection point through the angles. I know I can use Pythagoras, but was hoping to use something like GPC, but this works only for polygons?
Lug Horizontal.sm
#2 Опубликовано: 18.07.2020 13:42:58
Try a short circle code.
1 пользователям понравился этот пост
frapuano 18.07.2020 16:52:00
#3 Опубликовано: 18.07.2020 19:09:52
#4 Опубликовано: 19.07.2020 06:39:06
Hi Jean,
I will have a look, I'm sure I can use something.
Thanks
I will have a look, I'm sure I can use something.
Thanks
#5 Опубликовано: 20.07.2020 05:24:38
1 пользователям понравился этот пост
Alvaro Diaz Falconi 21.07.2020 13:49:00
#6 Опубликовано: 20.07.2020 08:34:13
Whereas the system is built scalar wrt θ
make it more convenient local at graph display.
Lug Horizontal_2.sm
make it more convenient local at graph display.
Lug Horizontal_2.sm
#7 Опубликовано: 20.07.2020 13:46:20
This provides the shortest distance from the segments of the polygon to the circle. However, the distance isn't really to the segment but to a line through the endpoints of the segment. There is no test if the normal to the line through c is between the vertices of the segment.
For the given geometry this works. For proof of strength this is only useful if a given force may act under any angle but the force doesn't depend on that angle.
Lug Horizontal_Kr.sm
For the given geometry this works. For proof of strength this is only useful if a given force may act under any angle but the force doesn't depend on that angle.
Lug Horizontal_Kr.sm
Martin Kraska
Pre-configured portable distribution of SMath Studio: https://en.smath.info/wiki/SMath%20with%20Plugins.ashx
2 пользователям понравился этот пост
#8 Опубликовано: 21.07.2020 02:25:44
Hi All,
Trying to work out a universal way of getting the length of intersecting lines, easy when lines are level, but not so (for me) others.
...
Hi. Your request it's about a complex computer graphic problem. This is a page for an undergraduated course: https://www.fing.edu.uy/inco/cursos/compgraf/
This paper have a pseudo code for solve partially your problem:
http://www.itseng.org/research/papers/topics/VLSI_Physical_Design_Automation/Physical_Verification/DRC/Geometric_Intersection_Problems/1979-Bentley.pdf
Hope that's helps.
Alvaro.
1 пользователям понравился этот пост
frapuano 21.07.2020 07:03:00
#9 Опубликовано: 21.07.2020 02:44:11
ianlh, in your example it’s convenient to use the rotation matrix
Lug Horizontal1.sm
Hi. This is what's actually do the Ber'f function:
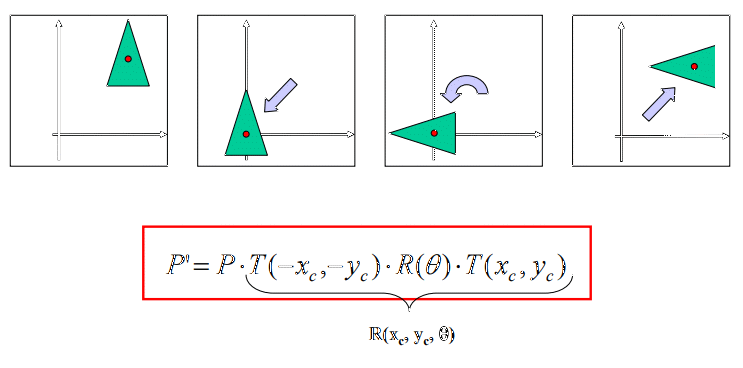
But notice that for use matrix multiplication for translations you must to use homogeneous coords ( http://elopez.fime.uanl.mx/@materias/732/@Tema%203%20-%20Transformaciones%202D.pdf page 15)
Best regards.
Alvaro.
2 пользователям понравился этот пост
#10 Опубликовано: 21.07.2020 07:37:50
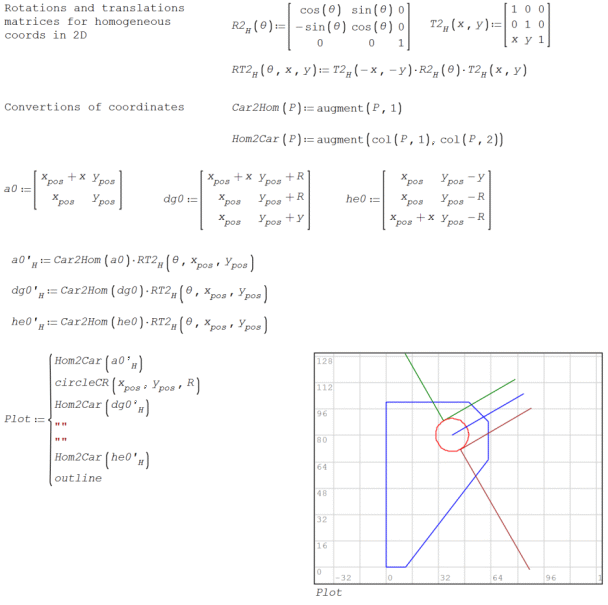
Thank you, Razonar.Aapplying homogeneous coordinates helps automate the process.
Variant with homogeneous coordinates
Lug Horizontal3.sm
Variant with homogeneous coordinates
Lug Horizontal3.sm
2 пользователям понравился этот пост
#11 Опубликовано: 21.07.2020 14:15:57
...
Variant with homogeneous coordinates ...
Another variant.
Lug Horizontal4.sm
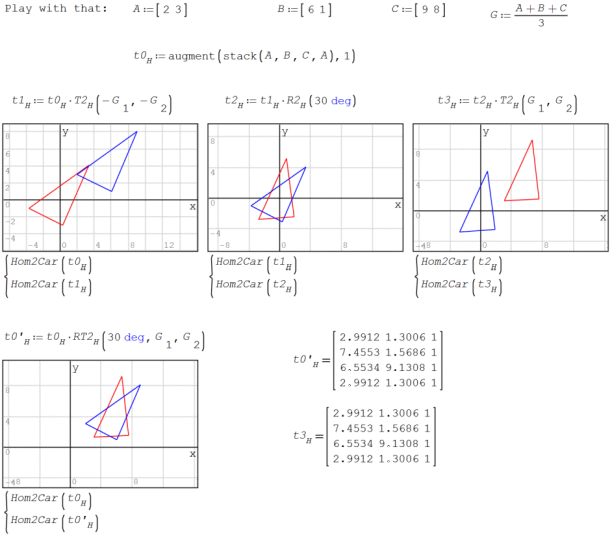
Homogeneous coordinates are helpful in projective geometry and conics and quadrics. For instance, preserve the duality, because you can use line coordinates ( https://en.wikipedia.org/wiki/Line_coordinates ).
I try to modify for use that in https://en.smath.com/forum/yaf_postst17357_Conics.aspx but can't found a close end. This is my atemp for the dual of a conic, it's envelope:
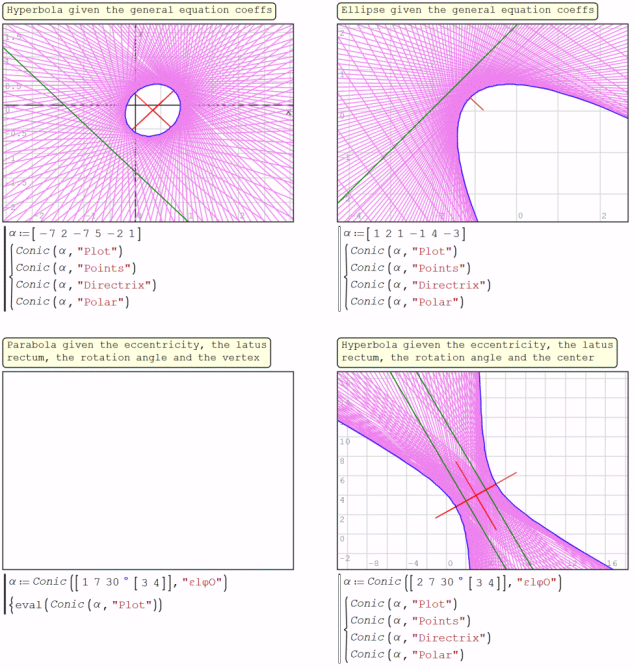
Best regards.
Alvaro
2 пользователям понравился этот пост
#13 Опубликовано: 27.07.2020 00:37:33
Hi Ber. That's not science, that's art. Maybe you can find this book interesting: Modern Robotics.
At page 608 in the pdf, for example:
The notation isn't the best, but it can be converted to a general Rotations and translations for the forward kinematics of a robot.
Best regards.
Alvaro.
At page 608 in the pdf, for example:
The notation isn't the best, but it can be converted to a general Rotations and translations for the forward kinematics of a robot.
Best regards.
Alvaro.
2 пользователям понравился этот пост
#14 Опубликовано: 27.07.2020 05:31:15
Hello Razonar. "Modern Robotics" book
sparked my big interest. Thank you for the link.
sparked my big interest. Thank you for the link.
-
Новые сообщения
-
Нет новых сообщений