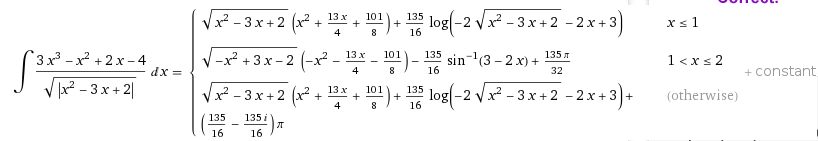1 страниц (11 вхождений)
Definite integral - "x - not defined" ? - Сообщения
Hello,
I have the following problem, trying to solve the definite integral int((3*x^3-x^2+2*x-4)/sqrt(x^2-3*x+2),dx,0,1): I get the error "x - not defined" and, of course, no result.
If I change the limits to [0..401], I get a result (!) with no error message, but if I set the upper limit lower than 401, I get the error again...
What is the reason for that?
Thanks in advance for your replies.
Conrad
I have the following problem, trying to solve the definite integral int((3*x^3-x^2+2*x-4)/sqrt(x^2-3*x+2),dx,0,1): I get the error "x - not defined" and, of course, no result.
If I change the limits to [0..401], I get a result (!) with no error message, but if I set the upper limit lower than 401, I get the error again...
What is the reason for that?
Thanks in advance for your replies.
Conrad
WroteThe integrand is undefined @ x = 1
Three verdicts in there:
1. Nothing will integrate that freak above x=1.9999999999999999999999999999
2. Nothing will integrate up to x=0.99999999999999999999999999999999
3. Can only integrate in reasonable range of the integrand.
Interesting Classroom example ... always plot the integrand !!!
IntegrateFreak.sm (7,28 КиБ) скачан 656 раз(а).
Hello Conrad,
Often, it is possible to improve the Smath native Simpson integrator.
Romberg is profitable in example 2 which looks easy from plotting
the integrand, but finally is not so.
Jean
Integrate Romberg Technical.sm (51,89 КиБ) скачан 658 раз(а).
Often, it is possible to improve the Smath native Simpson integrator.
Romberg is profitable in example 2 which looks easy from plotting
the integrand, but finally is not so.
Jean
Integrate Romberg Technical.sm (51,89 КиБ) скачан 658 раз(а).
Hi. I think that here the point is how to handle avoidable discontinuities in SMath. Because integral and other operators or functions not accept the 'if' statement, you can use 'cases' in the definition of f, as this:
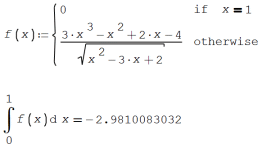
Even this isn't the case, this other is more general for avoiding numerical issues with avoidable discontinuities:
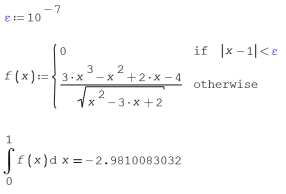
Best regards.
Alvaro.
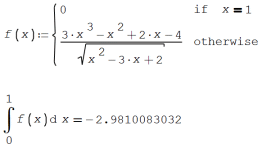
Even this isn't the case, this other is more general for avoiding numerical issues with avoidable discontinuities:
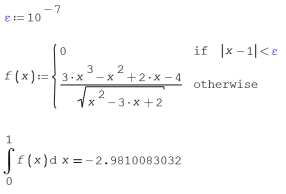
Best regards.
Alvaro.
1 пользователям понравился этот пост
sergio 08.02.2019 08:59:00
About the other discontinuity, at x=2, I guess that you don't want to work with complexes. It's usual take the absolute vale of logs and roots in real analysis calculus. This other isn't avoidable discont, but can be handled in a similar way.
discont_integral.sm (8,65 КиБ) скачан 663 раз(а).
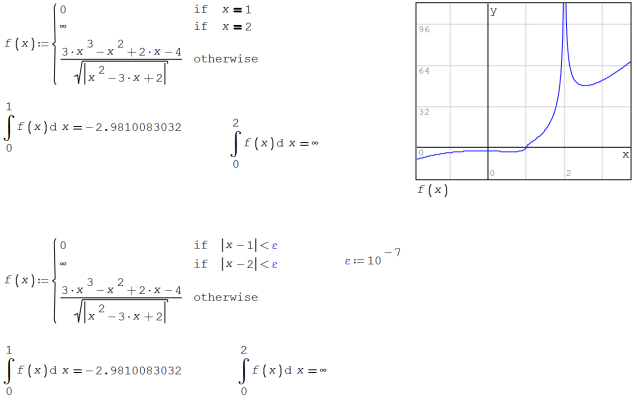
Best regards.
Alvaro.
discont_integral.sm (8,65 КиБ) скачан 663 раз(а).
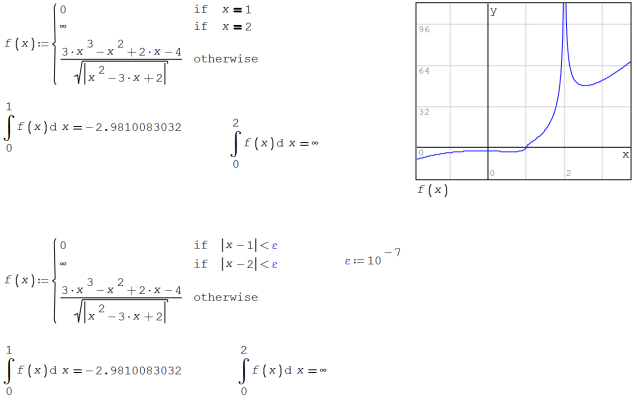
Best regards.
Alvaro.
3 пользователям понравился этот пост
Вячеслав Мезенцев 08.02.2019 08:30:00, frapuano 08.02.2019 09:52:00, NDTM Amarasekera 08.02.2019 12:14:00
maple() also can do that.
Файл не найден. Файл не найден.
Файл не найден. Файл не найден.
Russia ☭ forever, Viacheslav N. Mezentsev
2 пользователям понравился этот пост
Wrotemaple() also can do that.
maple [0..1] = -2.98126694400594
Mathcad 11 [0..1]= -2.98126694400554
Smath = -2.98126668567898 ... acc 10000
This is a case of singular end point
WroteThat's means that numerical procedure for computing int in SMath needs some improvements.
That's an old long due request.
At least, we have the adaptive from Carlos
Romberg algo style works well, very useful too.
1 страниц (11 вхождений)
- Новые сообщения
- Нет новых сообщений