1 страниц (16 вхождений)
solving equation within a range and integral - Сообщения
Good day!
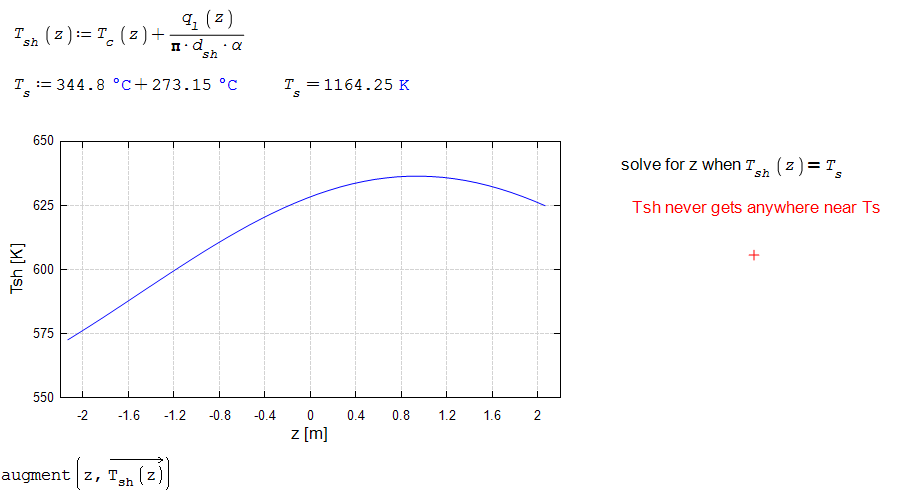
I was a Mathcad Prime user but I am currently trying to learn SMath and importing my calculations in it. It was easier in Mathcad but somehow I'm stuck when doing this part regarding solving equation that involves units, a range, and integral, and graphing the plots
I would really appreciate if someone could help me with my problem

solver.sm (10,71 КиБ) скачан 552 раз(а).
I was a Mathcad Prime user but I am currently trying to learn SMath and importing my calculations in it. It was easier in Mathcad but somehow I'm stuck when doing this part regarding solving equation that involves units, a range, and integral, and graphing the plots
I would really appreciate if someone could help me with my problem

solver.sm (10,71 КиБ) скачан 552 раз(а).
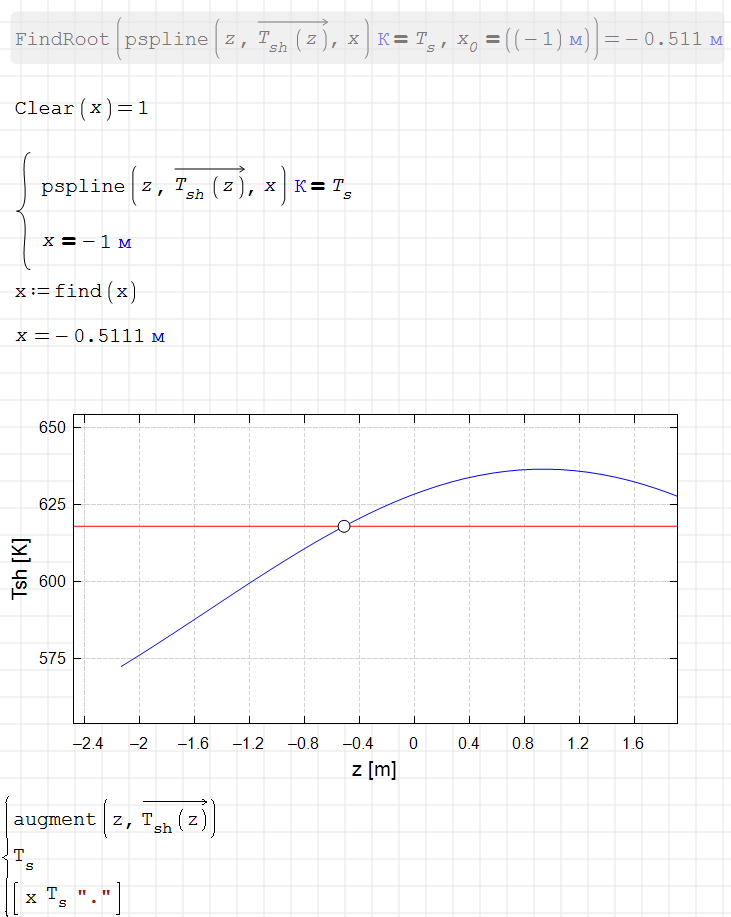
Hi. You can try using some ad-hoc Newton-Raphson method.
solver_mule.sm (17,92 КиБ) скачан 528 раз(а).
Best regards.
Alvaro.
solver_mule.sm (17,92 КиБ) скачан 528 раз(а).

Best regards.
Alvaro.
1 пользователям понравился этот пост
mule 10.09.2025 12:11:35
@mule You are right! It's what SMath returned, and I didn't do a sanity check! Of course, SMath understands units - I'm obviously half asleep today!!
I simply wrote a simple Newton-Raphson solution in the attached.
solver_b.sm (18,29 КиБ) скачан 604 раз(а).
I simply wrote a simple Newton-Raphson solution in the attached.
solver_b.sm (18,29 КиБ) скачан 604 раз(а).
Отредактировано 09.09.2025 16:18:54
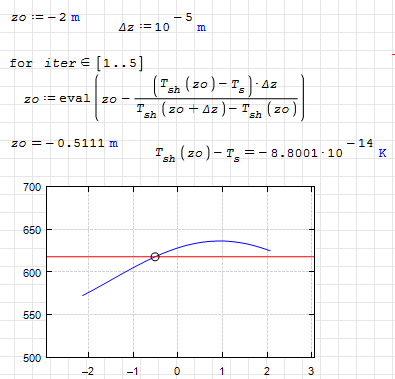
Sometimes just sampling and interpolating the function helps.
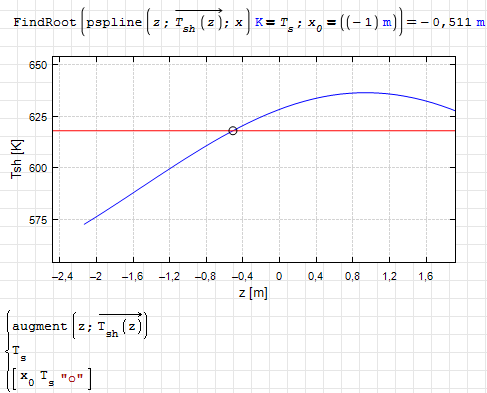
solver_b_Kr.sm (21,06 КиБ) скачан 571 раз(а).

solver_b_Kr.sm (21,06 КиБ) скачан 571 раз(а).
Martin KraskaPre-configured portable distribution of SMath Studio: https://en.smath.info/wiki/SMath%20with%20Plugins.ashx
3 пользователям понравился этот пост
Russia ☭ forever, Viacheslav N. Mezentsev
3 пользователям понравился этот пост
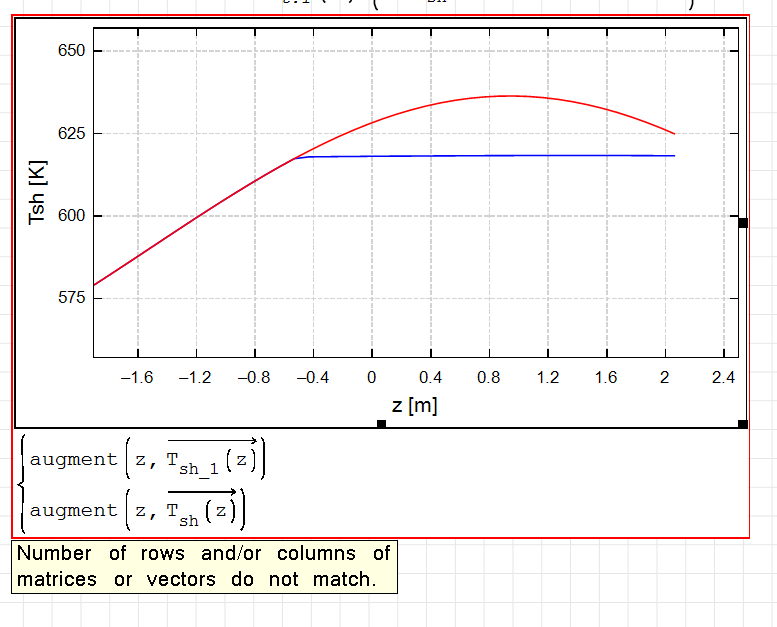
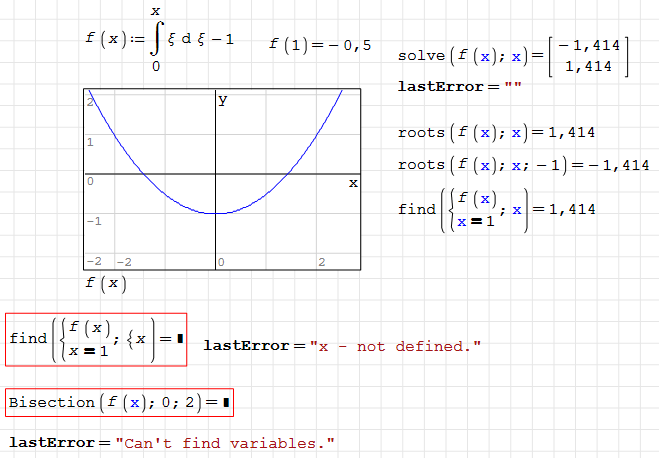
Is anyone able to explain, why the function can be evaluated in the context of pspline but not in the context of a solver? Looks like a really big problem under the hood, otherwise could have been fixed long ago.
Edit: Part of the problem is throwing pointless error messages. The unknown variable MUST be undefined in solver calls.
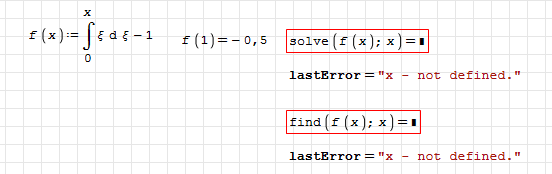
Edit: Part of the problem is throwing pointless error messages. The unknown variable MUST be undefined in solver calls.

Отредактировано 10.09.2025 07:41:00
Martin KraskaPre-configured portable distribution of SMath Studio: https://en.smath.info/wiki/SMath%20with%20Plugins.ashx
I can make an assumption that the integral with a parameter in the upper limit works only for numerical calculations, and is not supported for symbolic transformations.
Russia ☭ forever, Viacheslav N. Mezentsev
As far as I understand, all solvers are numeric procedures, except roots(), where I suspect that it tries to determine the gradient symbolically. Even the gradient-free Bisection() fails. Here I can't understand why any symbolic evaluation should be required.
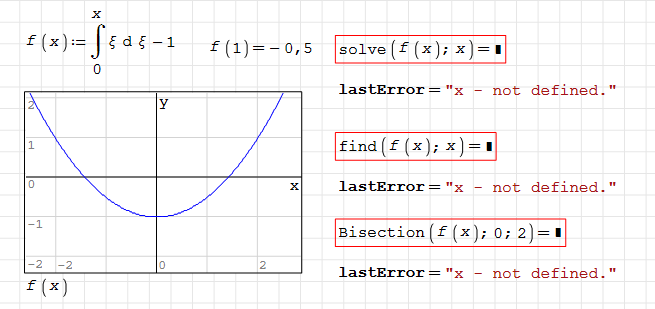

Martin KraskaPre-configured portable distribution of SMath Studio: https://en.smath.info/wiki/SMath%20with%20Plugins.ashx
In fact, when implementing a function in a plugin, you have the opportunity to do preliminary transformations before the actual numerical calculations begin.
Very rarely is the implementation of a function purely numerical. Moreover, for any functions that accept expressions, the implementation always contains symbolic transformations.
Look at how the pspline function is implemented
It is a completely numerical function, since it works with scalars. It does not perform symbolic transformations and when it is necessary to calculate an integral, it becomes defined with specific limits in the form of numbers. The equation solver sees an unfamiliar function and simply assumes that it works.
Very rarely is the implementation of a function purely numerical. Moreover, for any functions that accept expressions, the implementation always contains symbolic transformations.
Look at how the pspline function is implemented
public bool TryEvaluateExpression( Entry value, Store context, ref Entry result ) => false;It is a completely numerical function, since it works with scalars. It does not perform symbolic transformations and when it is necessary to calculate an integral, it becomes defined with specific limits in the form of numbers. The equation solver sees an unfamiliar function and simply assumes that it works.
Отредактировано 10.09.2025 11:06:08
Russia ☭ forever, Viacheslav N. Mezentsev
1 пользователям понравился этот пост
Martin Kraska 10.09.2025 20:56:36
WOW! it's exactly as what I did with Mathcad Prime. Thank you very much for this tip. I'm definitely using SMath from now on
WroteFunny workaround. Other solvers are now available.
solver_b_Kr_uni.sm (23,2 КиБ) скачан 543 раз(а).
WroteAs far as I understand, all solvers are numeric procedures, except roots(), where I suspect that it tries to determine the gradient symbolically. Even the gradient-free Bisection() fails ...
Hi Martin. The "symbolic" part in all the solvers in the NonLinearSolvers plugin is Unknowns. You can see from Bisection's syntax that it has to use it to determine which is the independent variable. In other words, if Unknowns fails, the solver fails too.
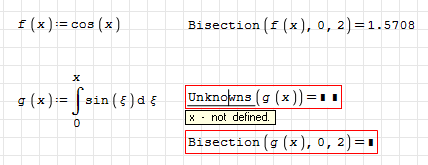
Best regards.
Alvaro.
1 пользователям понравился этот пост
Martin Kraska 10.09.2025 20:56:28
Alvaro, I see that Unknowns() just is not smart enough. Yet, this does not apply to the solvers which do not need to guess the names of the variables,
Viatcheslav, you pointing to the scalar nature of the argument (the third one) of pspline() brought an argument to my mind that I once had with Andrey. I complained that SMath doesn't perform some symbolic simplifications (see screenshot below) and the essence of that discussion was that Maxima assumes unknown variables to be scalars, while SMath doesn't do that. Andrey insisted in not making the scalarity assumption by default.
Yet, there is a way in SMath to declare a variable as scalar: you have to tag it as unit.
And indeed, this trick does the job for solve() and roots() and find(). Yet I consider this rather being a hack than a solution.
First, you frequently have naming conflicts with pre-defined units.
Second, I can't explain to the reader, why a solver which anyways can't handle anything except scalars (like solve()) doesn't make that assumption by default.
find() seems to have the best unit handling. The unknowns are allowed to have units and be tagged as units. Yet, having the scalarity assumption in it by default, would be a dream.
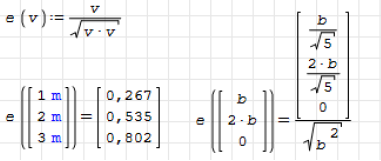
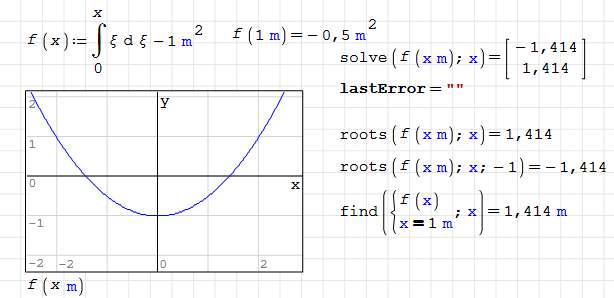
Viatcheslav, you pointing to the scalar nature of the argument (the third one) of pspline() brought an argument to my mind that I once had with Andrey. I complained that SMath doesn't perform some symbolic simplifications (see screenshot below) and the essence of that discussion was that Maxima assumes unknown variables to be scalars, while SMath doesn't do that. Andrey insisted in not making the scalarity assumption by default.
Yet, there is a way in SMath to declare a variable as scalar: you have to tag it as unit.
And indeed, this trick does the job for solve() and roots() and find(). Yet I consider this rather being a hack than a solution.
First, you frequently have naming conflicts with pre-defined units.
Second, I can't explain to the reader, why a solver which anyways can't handle anything except scalars (like solve()) doesn't make that assumption by default.
find() seems to have the best unit handling. The unknowns are allowed to have units and be tagged as units. Yet, having the scalarity assumption in it by default, would be a dream.
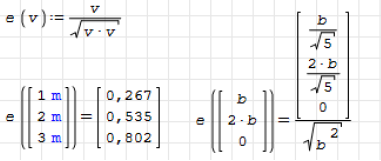

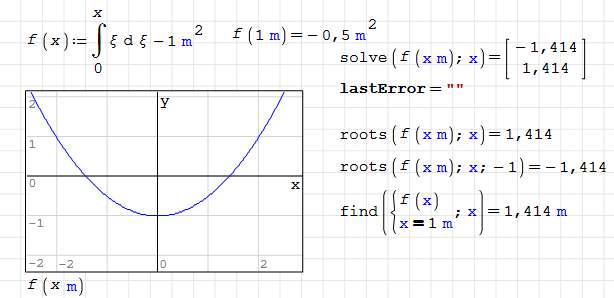
Martin KraskaPre-configured portable distribution of SMath Studio: https://en.smath.info/wiki/SMath%20with%20Plugins.ashx
1 пользователям понравился этот пост
Вячеслав Мезенцев 10.09.2025 21:11:08
1 страниц (16 вхождений)
- Новые сообщения
- Нет новых сообщений