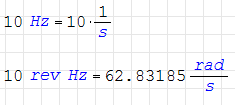1 страниц (14 вхождений)
Problem in the units conversion [frequence] - The software doesn´t distingue the units [rad/s] and [hz] - Сообщения
Hi,
I work with smath and I discovered that the software doesn´t distingue the units [rad/s] and [hz].
I found this when I put a value with the unit rpm [revolution per minute] and ask to smath convert to hz [revolution per second]. The conversion is: [rpm] * (pi / 30) = [hz] = [rad/s]. This conversion is correct to [rad/s], but to convert [rpm] to [hz] the operation is: [rpm] * (1/60) = [hz] .
thanks!
I work with smath and I discovered that the software doesn´t distingue the units [rad/s] and [hz].
I found this when I put a value with the unit rpm [revolution per minute] and ask to smath convert to hz [revolution per second]. The conversion is: [rpm] * (pi / 30) = [hz] = [rad/s]. This conversion is correct to [rad/s], but to convert [rpm] to [hz] the operation is: [rpm] * (1/60) = [hz] .
thanks!
Hello
Please look at this post
http://en.smath.info/forum/yaf_postsm8896_units-definition-file.aspx#post8896
Please look at this post
http://en.smath.info/forum/yaf_postsm8896_units-definition-file.aspx#post8896
I understood that smath uses the unit [rad/s] as default. But the definition of hertz still wrong.
The right definition is :
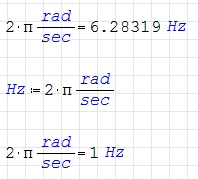
1 [hz] = 2*pi [rad/s]
The wrong definition that the software uses is :
1 [hz] = 1 [rad/s]
The right definition is :
1 [hz] = 2*pi [rad/s]
The wrong definition that the software uses is :
1 [hz] = 1 [rad/s]
You are right. I'm really confused. 
This seems a common confusion as explained in this article
http://en.wikipedia.org/wiki/Radian_per_second
which says right after the table :
I would like to hear other forum member's opinions about this question.
For now, you always can redefine Hz:=2π rad/sec
This seems a common confusion as explained in this article
http://en.wikipedia.org/wiki/Radian_per_second
which says right after the table :
Цитата
Note that because the radian is a dimensionless unit, the radian per second is dimensionally equivalent to the hertz—both are defined as one s−1. This means that great care must be taken to avoid confusing angular frequency ω and frequency ν.
I would like to hear other forum member's opinions about this question.
For now, you always can redefine Hz:=2π rad/sec

There are lots of quantities with identical dimensionality but still different physical meaning out there. Frequency and angular velocity are just examples for that. Another instance of dimension 1/s is the strain rate (strain being dimensionless as the ratio of length change to length). Strain is given in %, without unit or with µm/m or mm/m. The latter are interesting in that they provide intuitive reference to the quantities definition and include convenient decimal factors.
The confusion with rad/s and Hz arises from confusion between angular velocity (also known as angular frequency) and frequency. Frequency is the count of some cyclic events within a given time.
If the event is the completion of a full turn of some body, than you may call that event revolution or cycle and measure the corresponding frequency in rpm or if you refer to a second as time interval, then the unit would be rps, which is not common and not pre-defined in SMath, because Hz is an appropriate equivalent for that.
If the event is the completion of one radiant angular motion (an object at one length unit radius having travelled an arc length of the same unit), then the frequency is called angular frequency or angular velocity and should not be measured in Hz, just as the strain rate would be senseless to measure in Hz. Rotation by one radiant is no way more cyclic than linear motion by an arbitrary unit of length.
The clean solution is to accept the factor of 2п between frequency and angular velocity (or angular frequency). In my handbook (link in signature, see section 6.6, pages 95ff) I list the units rpm, rph and radpm as units of angular velocity and Hz and its derivates KHz, GHz, MHz as units of frequency.
Transformations between these quantities are consistently done using the definition of a revolution. SMath provides the angular unit 'rev := 2п. Thus Hz = rev/s holds true.
EDIT: Not quite correct. Better: Displaying an angular velocity in rev/s gives the frequency value in Hz.
I consider the SMath unit system being consistent and set up very well.
The confusion with rad/s and Hz arises from confusion between angular velocity (also known as angular frequency) and frequency. Frequency is the count of some cyclic events within a given time.
If the event is the completion of a full turn of some body, than you may call that event revolution or cycle and measure the corresponding frequency in rpm or if you refer to a second as time interval, then the unit would be rps, which is not common and not pre-defined in SMath, because Hz is an appropriate equivalent for that.
If the event is the completion of one radiant angular motion (an object at one length unit radius having travelled an arc length of the same unit), then the frequency is called angular frequency or angular velocity and should not be measured in Hz, just as the strain rate would be senseless to measure in Hz. Rotation by one radiant is no way more cyclic than linear motion by an arbitrary unit of length.
The clean solution is to accept the factor of 2п between frequency and angular velocity (or angular frequency). In my handbook (link in signature, see section 6.6, pages 95ff) I list the units rpm, rph and radpm as units of angular velocity and Hz and its derivates KHz, GHz, MHz as units of frequency.
Transformations between these quantities are consistently done using the definition of a revolution. SMath provides the angular unit 'rev := 2п. Thus Hz = rev/s holds true.
EDIT: Not quite correct. Better: Displaying an angular velocity in rev/s gives the frequency value in Hz.
I consider the SMath unit system being consistent and set up very well.
Martin KraskaPre-configured portable distribution of SMath Studio: https://en.smath.info/wiki/SMath%20with%20Plugins.ashx
1 пользователям понравился этот пост
Davide Carpi 03.04.2013 14:04:00
Thanks Martin for your explanation though I still have to read the reference on your handbook to fully understand this matter.
I've made some tests on the attached sheet, the cells remarked in yellow are thought to be incorrect whereas the cells in green should be expected as correct.
Hz_unit.sm (8,92 КиБ) скачан 742 раз(а).
I've made some tests on the attached sheet, the cells remarked in yellow are thought to be incorrect whereas the cells in green should be expected as correct.
Hz_unit.sm (8,92 КиБ) скачан 742 раз(а).
Wrote
Transformations between these quantities are consistently done using the definition of a revolution. SMath provides the angular unit 'rev := 2п. Thus Hz = rev/s holds true.
Actually in SMath Hz is not equal to rev/s.
That's why I suggested to redefine this way in the above sheet.
I agree with kilele´s suggestion...
Thanks!!
Thanks!!
Beat count is 10 per second. How would I express this in SMath? 10/s is a natural way. And I expect this to be 10Hz. It's no wonder that Hz is defined as 1/s. But as radian is dimensionless unit, and is basic unit for angles in SI (and SMath), and thus is defined as 1, it is possible to write 10rad/s=10Hz. This is a logical error, and it cannot be solved by redefinition of either Hz as 2π/s (or else 10Hz will become 62.8319/s), nor radian (as this would violate the fundamental meaning of radian being ratio of arc lenth to radius). The human must take care when frequencies are used, and when angular velocities are.
Another example of dimensionless unit is slope (ratio of horizontal distance to elevation). It may be, say, 1/1000 (1 mm elevation per 1 meter distance). It is another angular measure; and it's incorrect to expect that SMath will be able to guess that a variable that holds 0.001 means tangent of an angle, and not the angle measured in radians. Improper mixture of those units will give wrong results, but it's pure human error.
Another example of dimensionless unit is slope (ratio of horizontal distance to elevation). It may be, say, 1/1000 (1 mm elevation per 1 meter distance). It is another angular measure; and it's incorrect to expect that SMath will be able to guess that a variable that holds 0.001 means tangent of an angle, and not the angle measured in radians. Improper mixture of those units will give wrong results, but it's pure human error.
С уважением,
Михаил Каганский
1 пользователям понравился этот пост
Davide Carpi 03.04.2013 14:04:00
Eppur si muove..
No, seriously I think I get your point.
Hz and rad/s measure different magnitudes, therefore Hugo's question was posed in the wrong way.
No, seriously I think I get your point.
Hz and rad/s measure different magnitudes, therefore Hugo's question was posed in the wrong way.
Radians is usually thought of as a unitless ratio and an angle. Really it is not. Physically it is a self-aligning, normalized unit of distance. The one unit meter is a standard unit of distance for all the world and its one and only perfect prototype is sitting in a vault in france. All units of distance referring to meters is calculated against this prototype length by taking a raw measured distance and (theoretically) dividing it by the prototype length (i.e., breaking the raw length into a bunch of distinct meter prototype long segments and a fractional remainder and then counting up all the segments) to yield a distance in meters. Is this ratio of raw length over meter prototype length unitless? No. Rather, the ratio is defined as a unit.
Radians is not a standard length with a perfect prototype like the meter, but it is a unit of distance like the meter. It is a scalable unit of distance. It is used as a measure of length for measures of arc distance where the prototype length is the length of the circle's radius (the circle being the one upon which the arc distance is being measured). This is not a unitless ratio as is taught. It is a distance made by segmenting the arc into sections, each one radius long and a fractional remainder and then counting up all the segments. This unit of length is called a radian. It is physical.
Angle is taught as a ratio called radians. This just confuses the issue. Degrees are truly angles as they are not tied to any length, but are a "linearized" ratio of rise over run (i.e., a linearization of the tangent ratio). Gradians are similar to degrees, but represent the angle as a linear percentage from perfectly parallel alignment to perpendicular. Radians may be treated as an angle and we are taught to see them that way, but they are truly a measure of length and therefore are not unitless as an angle truly is. It just looks that way because of the slick way the radian length was defined.
It seems to me that one factor in the solution to properly representing radians vs hertz is to have a pseudo unit (geometric unit?) called radius as a predefined entity. Assignment of a value with the radius unit would tell smath what radius length (in meters or other) is in force. Similarly, arc length and arc velocity could be defined. These geometric units (circular units?) would allow smath to keep proper track of what's going on and then be used to properly convert between hertz and radians with the 2PI factor properly enforced inside smath. I haven't thought this all the way through, but this is the germ of the idea.
Radians is not a standard length with a perfect prototype like the meter, but it is a unit of distance like the meter. It is a scalable unit of distance. It is used as a measure of length for measures of arc distance where the prototype length is the length of the circle's radius (the circle being the one upon which the arc distance is being measured). This is not a unitless ratio as is taught. It is a distance made by segmenting the arc into sections, each one radius long and a fractional remainder and then counting up all the segments. This unit of length is called a radian. It is physical.
Angle is taught as a ratio called radians. This just confuses the issue. Degrees are truly angles as they are not tied to any length, but are a "linearized" ratio of rise over run (i.e., a linearization of the tangent ratio). Gradians are similar to degrees, but represent the angle as a linear percentage from perfectly parallel alignment to perpendicular. Radians may be treated as an angle and we are taught to see them that way, but they are truly a measure of length and therefore are not unitless as an angle truly is. It just looks that way because of the slick way the radian length was defined.
It seems to me that one factor in the solution to properly representing radians vs hertz is to have a pseudo unit (geometric unit?) called radius as a predefined entity. Assignment of a value with the radius unit would tell smath what radius length (in meters or other) is in force. Similarly, arc length and arc velocity could be defined. These geometric units (circular units?) would allow smath to keep proper track of what's going on and then be used to properly convert between hertz and radians with the 2PI factor properly enforced inside smath. I haven't thought this all the way through, but this is the germ of the idea.
1 пользователям понравился этот пост
Davide Carpi 03.04.2013 14:04:00
Any unit is defined to be a divider to the corresponding quantities. But radians differ from meters much greater then degrees. Both meters and degrees are defined using some static values. (Side note: meter is not defined as length of a French sample anymore.) But the radian is defined in the terms of a characteristic of an object it measures (radius), and thus its definition is "contextual" (in a sense).
The radian is truly angle, like it or not. The corresponding length unit is not called "radian"; it is called "radius". And the radian is the ANGLE that is defined by the arc of that length. Don't try to oversimplify things where it's not proper.
Angles measured in radians are constructed not in terms of arc lengths; they are multiples of the reference angle (1 radian) that is DEFINED dimensionless. If they were multiples of a DIMENSIONED unit, then they had dimension themselves.
When I wrote that radian is ratio of arc length to radius, I only meant the numerical definition of the unit. I want to emphasize it once more: radian is defined dimensionless (the unit value itself is represented by ratio of one length to another), and so is any angle. This is unlike meter, that itself is not defined as ratio of same-dimensioned values.
SMath strictly follows SI; you may use whatever reasons, but doing it other way is bad idea. You better vote for changes in SI (however, I don't feel it to be a great proposal).
The radian is truly angle, like it or not. The corresponding length unit is not called "radian"; it is called "radius". And the radian is the ANGLE that is defined by the arc of that length. Don't try to oversimplify things where it's not proper.
Angles measured in radians are constructed not in terms of arc lengths; they are multiples of the reference angle (1 radian) that is DEFINED dimensionless. If they were multiples of a DIMENSIONED unit, then they had dimension themselves.
When I wrote that radian is ratio of arc length to radius, I only meant the numerical definition of the unit. I want to emphasize it once more: radian is defined dimensionless (the unit value itself is represented by ratio of one length to another), and so is any angle. This is unlike meter, that itself is not defined as ratio of same-dimensioned values.
SMath strictly follows SI; you may use whatever reasons, but doing it other way is bad idea. You better vote for changes in SI (however, I don't feel it to be a great proposal).
С уважением,
Михаил Каганский
And about the "linearized tangent ratio". I doubt that I understand you very well, but I don't see degrees (and other proportional angle units) as linearization of ratio of rise over run. They are better defined in terms of dividing whole turn by an integer (360). Linearization of ratio of rise over run is tangent itself.
С уважением,
Михаил Каганский
1 страниц (14 вхождений)
- Новые сообщения
- Нет новых сообщений