Wrote

Still I get errors in SS 7251.

After I got this error with 7251, again I did a Clean re-installation, and all issues posted later occurred consequent to this.

Furthermore, a similar Clean re-installation of 7251 was done in my second laptop today, but errors continued to occur with same test worksheets except Jean's "Test_Gamma_7251_[6179].sm".

Therefore, I have no alternative but leave it to the developers to decide.

Wrote

Therefore, I have no alternative but leave it to the developers to decide.

Wait and see what Grand Doctors have to say.
Frechet PDF is another one that Simpson rejects.
In the attached, rescued in two ways.
When compatible, dn_GearsBDF is hyperfast, known accurate.
Thanks Collab for your contribution, most interesting.
Cheers ... jean

Integrate Frechet.sm (21 КиБ) скачан 37 раз(а).

Wrote

When compatible, dn_GearsBDF is hyperfast, known accurate.

It carries parameters as well, following a fitting session.

Integrate Frechet.sm (28 КиБ) скачан 38 раз(а).

Observed same problems even after a second Clean re-installation of 7251.
Consequently, I noticed that the Vectorize operator works correctly
when eval() function is used to evaluate alpha and beta of the Gamma function.
Otherwise, it gives incompatible results.
Has anybody experienced this issue?
Thank you Jean for the inspiration and encouragement.
Thank you Alvaro.
Any comments?

New_Test_Gamma.sm (14 КиБ) скачан 38 раз(а).

Wrote

Any comments?

New_Test_Gamma.sm (11 КиБ) скачан 33 раз(а).

Hi Nugegodage. I slightly modify your file, putting eval only where Mean appear. What I see rigth now, with your new file using eval, not before, is that there are not bug, and the "bad results" are because Mean can't be vectorized (or better say, isn't a good idea vectorize them), like any other function that take vectors or matrices as arguments.

Wrote

Otherwise, it gives incompatible results.

Not clear what's incompatible in the yellow/red brace.

Wrote

Observed same problems even after a second Clean re-installation of 7251.

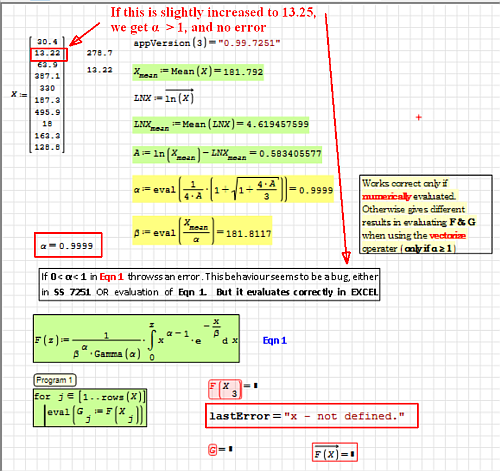
Gamma CDF function error revisited.
Following issues observed while trying to calculate SPI for a different set of data.

1. Gamma CDF function fails if 0 <'alpha' < 1
2. Even Razonar's method fails in such a situation.
3. According to the literature on calculation of SPI, the Gamma function is valid
for all 'alpha' values > 0.
4. No such issues in Excel or Mathcad.
5. Attached example is only to demonstrate the issue.

For the attention of authorities.

Gamma_CDF_Error_with_Alpha less than 1_.sm (13 КиБ) скачан 33 раз(а).

Wrote

Gamma CDF function fails

Your integration is ill posed ... "x_undefined"
SMath native Gamma(x) 4 decimals and INT acc 50 have no impact.
Try your own alpha/beta.
Cheers ... Jean

Page1 NDTMA.sm (13 КиБ) скачан 25 раз(а).

Wrote

Try your own alpha/beta.
Cheers ... Jean

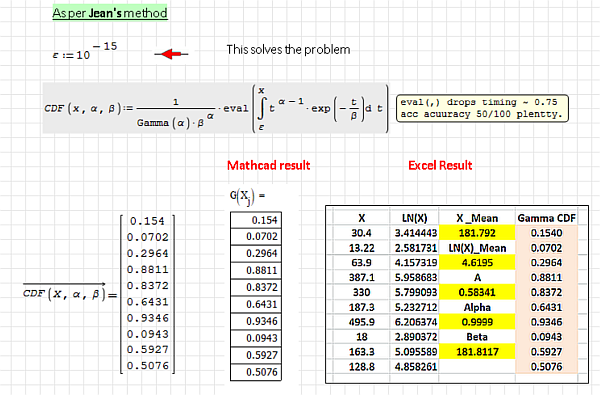
Thank you Jean. Your suggestion to introduce ε=10^{-15} as lower limit of integration
solved my problem. But still the error persists if lower limit is zero.
A beginner may be confused and/or discouraged in a similar situation.

Gamma_CDF_Error_with_Alpha less than 1_SOLVED.sm (106 КиБ) скачан 37 раз(а).

I see the issue... when alpha < 1 and t = 0 smath has 1/(0^(1-alpha)) and the numerical integrator fails. I'm not sure about how ccould be fixed.


Looking for improvements in the Gamma function...

Lanczos.sm (69 КиБ) скачан 38 раз(а).

Wrote

Looking for improvements in the Gamma function...

Thanks Davide: sanity check [real/complex] vs Keisan/Casio

All that is not as simple as the BigBang theory.
If the first computed 'x' appears in data < 10^-15
the quick plot rejects, no complain ... didn't check X_Y plot.
Thus: zero min value 10^-15.
Just experimented on Bézier/Bernstein project.
Cheers ... Jean

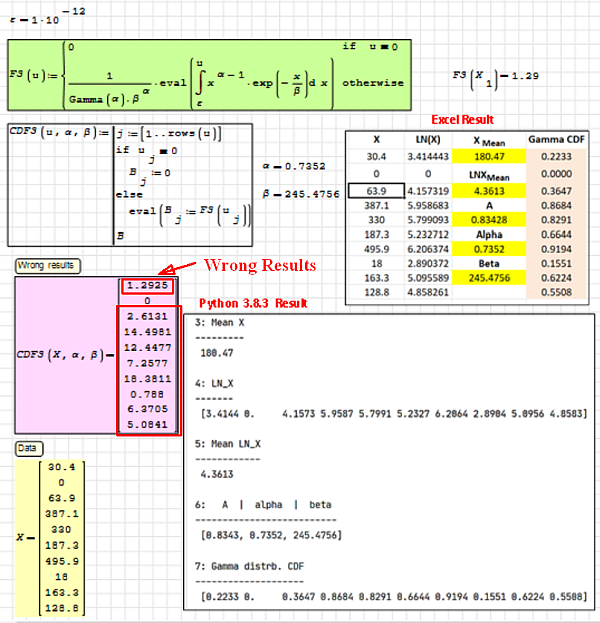
Wrote

Looking for improvements in the Gamma function..

A few more issues please.



Gamma_CDF_Error_Wrong_Results.sm (334 КиБ) скачан 32 раз(а).

Wrote

A few more issues please.

Freak 7251 does not open !
You just have two values: α:=0.7352, β:=245.7456
That's enough to simulate/evaluate CDF.
Cheers ... Jean

CDF Gamma.sm (262 КиБ) скачан 39 раз(а).

Wrote

Freak 7251 does not open !

Sorry. PDF attached. Thank you Jean!

Gamma_CDF_Error_Wrong_Results.pdf (953 КиБ) скачан 31 раз(а).

Ordinary Simpson is inadequate [too steep PDF, too long X's]
Romberg/Simpson algo style is just perfect.
All done in gray attached.
Cheers mon Ami from so far away !

CDF Gamma.sm (277 КиБ) скачан 37 раз(а).