1 страниц (8 вхождений)
Failing Newton-Raphson method due to "Units not matching" - Failing Newton-Raphson method due to "Units not matching" - Сообщения
Hello all,
I am relativly new to the program, and I've beeing trying to implement a Newton-Raphson method to evaluate force and moment equilibrium in a simple steel reinforced concrete element.
For this, I've tried implementing the .nonlinearsolvers plugin from Davide but with no avail. Due to this, I've beggun implementing the method in a manual fashion. For such compromise, I've studied the method, and found a few principles already discussed and made in the SMath's forum, which have led me to a better understanding and development of the feature.
Despite this, I'm still unnable to complete the method programming, due to 'units not matching' errors.
I've tried applying 'eval' function, but, probably due to my low experience with the program I haven't been sussessfull.
I will anex the Smath file if anyone is more experienced in the subject.
Any help is truly appreciated, as this is a learning experience for me.
Best Regards,
Tentativa de NewtonRaphson_2.sm (207,42 КиБ) скачан 1007 раз(а).
I am relativly new to the program, and I've beeing trying to implement a Newton-Raphson method to evaluate force and moment equilibrium in a simple steel reinforced concrete element.
For this, I've tried implementing the .nonlinearsolvers plugin from Davide but with no avail. Due to this, I've beggun implementing the method in a manual fashion. For such compromise, I've studied the method, and found a few principles already discussed and made in the SMath's forum, which have led me to a better understanding and development of the feature.
Despite this, I'm still unnable to complete the method programming, due to 'units not matching' errors.
I've tried applying 'eval' function, but, probably due to my low experience with the program I haven't been sussessfull.
I will anex the Smath file if anyone is more experienced in the subject.
Any help is truly appreciated, as this is a learning experience for me.
Best Regards,
Tentativa de NewtonRaphson_2.sm (207,42 КиБ) скачан 1007 раз(а).
Hi Joao,
Hoping to help you a little,
Regards,
Ioan
1. I noted your persistence on the forum, by waiting help on your problem – that seems now as not being the structural one but a mathematical one (?).
2. Seeing that during a previous exchange, I proposed to you a transparent and robust solution for your case – the dichotomy – that converge very well, I wonder why your perseverance on Newton-Raphson?
3. Starting from the assumption of “why not?” I propose to you, in the following, some comments.
4. The Newton Raphson suppose the use of the derivative of the function f(x) - the object of solution finding - I note that your f(x) function contains the "min(a;bb))" function. This function has no treatment in the SMath derivation procedure, that’s (IMHO) the main reason for your problems. However, seeing that under the min function there is a constant, that derived gives zero, you can produce externally the derivative. So, you can apply simply the Newton Raphson.
5. In order to make a more robust your solution finding process, I propose to make your f(x) parametric, by dividing it by b*h*fcd.
2. Seeing that during a previous exchange, I proposed to you a transparent and robust solution for your case – the dichotomy – that converge very well, I wonder why your perseverance on Newton-Raphson?
3. Starting from the assumption of “why not?” I propose to you, in the following, some comments.
4. The Newton Raphson suppose the use of the derivative of the function f(x) - the object of solution finding - I note that your f(x) function contains the "min(a;bb))" function. This function has no treatment in the SMath derivation procedure, that’s (IMHO) the main reason for your problems. However, seeing that under the min function there is a constant, that derived gives zero, you can produce externally the derivative. So, you can apply simply the Newton Raphson.
5. In order to make a more robust your solution finding process, I propose to make your f(x) parametric, by dividing it by b*h*fcd.
Hoping to help you a little,
Regards,
Ioan
Do to others as you would like them to do to you! Knowledge is of no value unless you put it into practice - Chekhov
@StvMath:
As you said, you hadn't understood the Joao's problem:
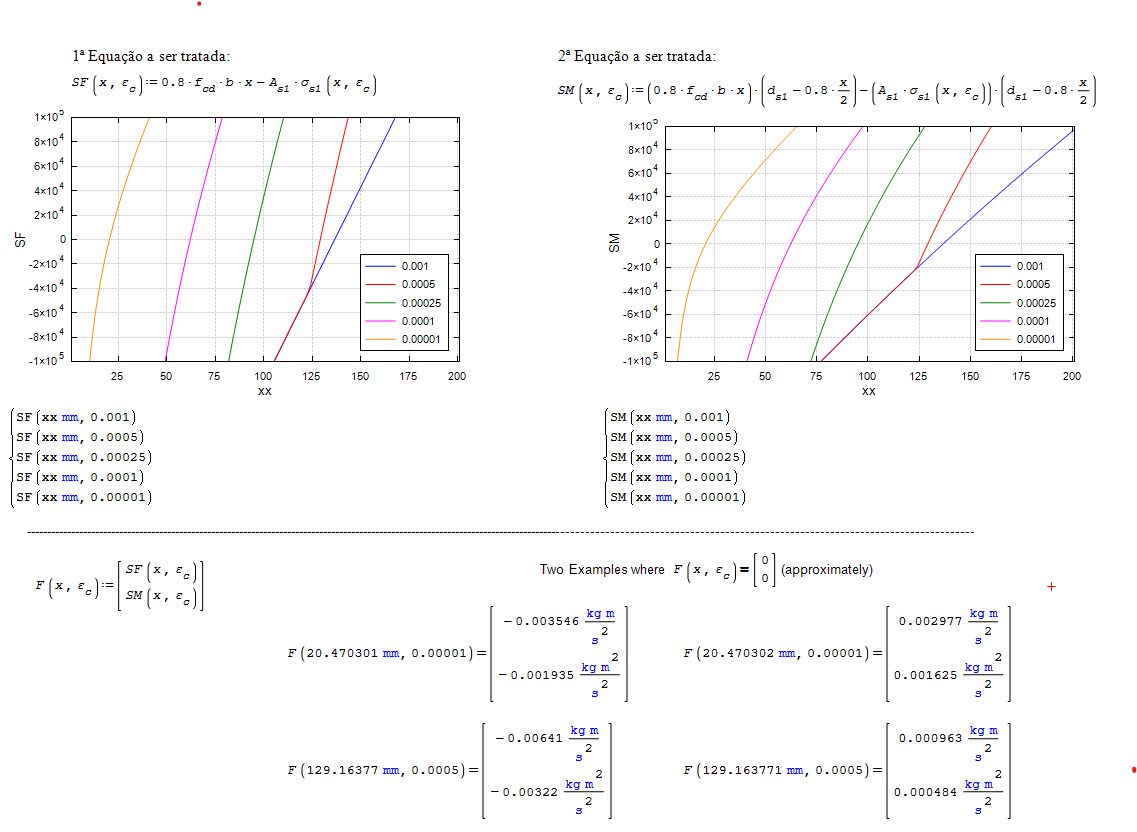
It is a classical reinforced concrete bending resistance for a rectangular section:
![2024-03-18 15_48_08-SMath Solver - [Tentativa de NewtonRaphson_2 (1).sm].png](/ru-RU/files/Download/rDNdpr/2024-03-18-15_48_08-SMath-Solver---[Tentativa-de-NewtonRaphson_2-(1).sm].png)
With some theoretical and normative assumptions, there is only one unknown "x" and it can be obtained from the bending moments equilibrium equation. All the Joao's development is correct.
The non-linearity of the problem comes from the non-linear behavior of materials.
As you said, you hadn't understood the Joao's problem:
It is a classical reinforced concrete bending resistance for a rectangular section:
![2024-03-18 15_48_08-SMath Solver - [Tentativa de NewtonRaphson_2 (1).sm].png](/ru-RU/files/Download/rDNdpr/2024-03-18-15_48_08-SMath-Solver---[Tentativa-de-NewtonRaphson_2-(1).sm].png)
With some theoretical and normative assumptions, there is only one unknown "x" and it can be obtained from the bending moments equilibrium equation. All the Joao's development is correct.
The non-linearity of the problem comes from the non-linear behavior of materials.
Do to others as you would like them to do to you! Knowledge is of no value unless you put it into practice - Chekhov
Wrote@StvMath:
As you said, you hadn't understood the Joao's problem:
With some theoretical and normative assumptions, there is only one unknown "x" and it can be obtained from the bending moments equilibrium equation. All the Joao's development is correct.
The non-linearity of the problem comes from the non-linear behavior of materials.
Thanks for the clarification.
However, there is a Newton-Raphson routine trying to find the zeros of SM and SF simultaneously. My previous post suggests there are an infinite number of possibilities for this! Or am I further misunderstanding?!!!
IMHO - In fact, ultimately there is only one non linear equation to deal with a mathematical solver. The two equations belong to an intermediary phase.
Do to others as you would like them to do to you! Knowledge is of no value unless you put it into practice - Chekhov
Tentativa de NewtonRaphson_3.sm (211,26 КиБ) скачан 1042 раз(а).Hello all,
First of all, I want to say my sincere thanks for the responses i've gotten, they push me into understanding my issue better and better.
Secondly, and sadly, I don't fully understand what the issue still is, and I don't think i've understood fully what was the issue of my previous formulation.
I've tried to further improve on my 'programmin', but I'm still presented with an "units not matching" error.
I'll provide, in anex, the corresponding file for possible further assistance.
Best regards,
First of all, I want to say my sincere thanks for the responses i've gotten, they push me into understanding my issue better and better.
Secondly, and sadly, I don't fully understand what the issue still is, and I don't think i've understood fully what was the issue of my previous formulation.
I've tried to further improve on my 'programmin', but I'm still presented with an "units not matching" error.
I'll provide, in anex, the corresponding file for possible further assistance.
Best regards,
WroteTentativa de NewtonRaphson_3.sm (211,26 КиБ) скачан 1042 раз(а).Hello all,
I'm still presented with an "units not matching" error.
The attached now runs (see the comments in red). However, your Newton-Raphson routine diverges. You will need to rethink your logic.
Tentativa de NewtonRaphson_3b.sm (215,56 КиБ) скачан 1018 раз(а).
1 страниц (8 вхождений)
- Новые сообщения
- Нет новых сообщений