I saw someone here doing simulations of pendulum and other nonlinear dynamic models, I wonder how can I do that on SMath given that solutions of the ODEs is known, thanks in advance

Wrote

I saw someone here doing simulations of pendulum and other nonlinear dynamic models, I wonder how can I do that on SMath given that solutions of the ODEs is known, thanks in advance

Number of ODE's have symbolic solution.
If your DE has either of these tree forms,
Smath will spits scalar solutions wrt parameters/IC ...
One of my old baby in Mathsoft Collaboratory.
Cheers ... Jean.

Thanks, But what I meant is how to simulate the pendulum motion itself seeing the bob and how it swings. See this link
https://en.smath.com/forum/yaf_postst973_Animation-double-pendulum-and-a-pendulum-on-a-spring.aspx

In the handbook section 8.2.6 (google for kraska smath handbuch) there is an example for such animations.

The idea is to parametrize your graphics expressions with the variable t and provide a vector of values for t via context menu of the graphic area. This only works for the built-in graphics region, not for x-y plot plugin and neither for maxima.

Wrote

In the handbook section 8.2.6 (google for kraska smath handbuch) there is an example for such animations.

The idea is to parametrize your graphics expressions with the variable t and provide a vector of values for t via context menu of the graphic area. This only works for the built-in graphics region, not for x-y plot plugin and neither for maxima.

Do you have a version that is in English?

Wrote

Do you have a version that is in English?

Google translate is your friend..
https://translate.google.com/?sl=de&tl=en&op=translate&hl=en

Wrote

Do you have a version that is in English?

No, but online translators nowadays are quite powerful.

Wrote

Thanks, But what I meant is how to simulate the pendulum motion itself seeing the bob and how it swings. See this link

Ber7 demos are 6 years before I joined Smath Community.
In the mean time, you can solve the homogeneous pendulum.
Cheers ... Jean.

ODE Pendulum Copy.sm (63 КиБ) скачан 28 раз(а).

Wrote

In the handbook section 8.2.6 (google for kraska smath handbuch) there is an example for such animations.

The idea is to parametrize your graphics expressions with the variable t and provide a vector of values for t via context menu of the graphic area. This only works for the built-in graphics region, not for x-y plot plugin and neither for maxima.

Finally, I did some animations, But I find some problems with the exported gifs. It acts like there are some missing frames while it's totally smooth inside the sheet.
Vibrating Pendulum.sm (15 КиБ) скачан 35 раз(а).

Wrote

...
Finally, I did some animations, But I find some problems with the exported gifs. It acts like there are some missing frames while it's totally smooth inside the sheet.
Vibrating Pendulum.sm (15 КиБ) скачан 35 раз(а).

Hi. This is a workaround for that bug: https://en.smath.com/forum/yaf_postsm75052_Problem-with-animated-gif-from-plot-region.aspx#post75052

However, notice that since the values of phi are numbers and not expressions, you cannot compute the derivatives of its components the way you do in D. You can check this by substituting zero for its values, and you get the same numerical solutions.





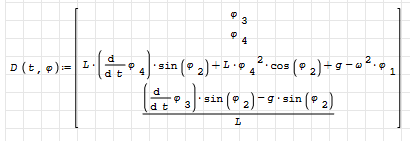
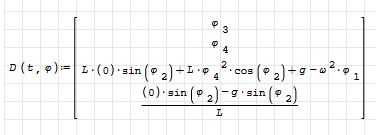
For diff(el(φ,3),t) you can use el(φ,4), and for diff(el(φ,4),t) you should use some kind of numerical estimate.

Best regards.
Alvaro.

Wrote

Wrote

...
Finally, I did some animations, But I find some problems with the exported gifs. It acts like there are some missing frames while it's totally smooth inside the sheet.
Vibrating Pendulum.sm (15 КиБ) скачан 35 раз(а).

Hi. This is a workaround for that bug: https://en.smath.com/forum/yaf_postsm75052_Problem-with-animated-gif-from-plot-region.aspx#post75052

However, notice that since the values of phi are numbers and not expressions, you cannot compute the derivatives of its components the way you do in D. You can check this by substituting zero for its values, and you get the same numerical solutions.





For diff(el(φ,3),t) you can use el(φ,4), and for diff(el(φ,4),t) you should use some kind of numerical estimate.

Best regards.
Alvaro.

I tried it, but still same bug exist maybe it got lowered but its still there and thanks for making me notice that mistake, does that mean we cannot solve numerically such type of DEs without assumptions?

Wrote

... does that mean we cannot solve numerically such type of DEs without assumptions?

Hi Oichi. Not. Remember that given F(x,x',x'',...,t) = 0 then for using numerical DEs solvers you must to find the system D(t,x) = [x', x'', ... ] with an appropriate change of variables. Which is your original analytic expression of your differential equation to be solved? This is, the one or two equations involving both all derivatives of all "x" variables, F(x,x',x'',...,t) = 0.

Best regards.
Alvaro.

This version is doctored for SS versions as low as SS 6179.
To make it compatible with ODE universal plugins.
Can you update my invented vector 'phi' in red
So that the system makes sense for all visitors.
Cheers ... Jean.

Vibrating Pendulum (1).sm (24 КиБ) скачан 29 раз(а).

Wrote

This version is doctored for SS versions as low as SS 6179.
To make it compatible with ODE universal plugins.
Can you update my invented vector 'phi' in red
So that the system makes sense for all visitors.
Cheers ... Jean.

Vibrating Pendulum (1).sm (24 КиБ) скачан 29 раз(а).

This example is for a pendulum that it's upper end is attached to a spring, The displacement of this upper end is Phi(1) "u" and the angular displacement of the pendulum is Phi(2) "theta". Phi(3) "u_dot" and Phi(4) "theta_dot" are the first derivatives of the upper end vertical motion and the angular displacement of the pendulum respectively.

I did a trick and removed the d/dt terms.. but now I got a new problem. The Adams function telling me "Cannot calculate"
Vibrating Pendulum 2.sm (107 КиБ) скачан 24 раз(а).

Wrote

This example is for a pendulum that it's upper end is attached to a spring, The displacement of this upper end is Phi(1) "u" and the angular displacement of the pendulum is Phi(2) "theta". Phi(3) "u_dot" and Phi(4) "theta_dot" are the first derivatives of the upper end vertical motion and the angular displacement of the pendulum respectively.

Thanks for explaining your advanced project.
Up until now, I can only manage the homogeneous Pendulum.
Cheers ... Jean.

Hi. The attached file uses the techniques shown here and here. You can also obtain the equations of motion using the lagrangian with what is shown here.

Vibrating Pendulum.sm (116 КиБ) скачан 35 раз(а).
Vibrating Pendulum.pdf (183 КиБ) скачан 36 раз(а).

Best regards.
Alvaro.

Wrote

Hi. The attached file uses the techniques shown here and here. You can also obtain the equations of motion using the lagrangian with what is shown here.

Vibrating Pendulum.sm (116 КиБ) скачан 35 раз(а).
Vibrating Pendulum.pdf (183 КиБ) скачан 36 раз(а).

Best regards.
Alvaro.

Thank you so much ^^, ODEs were already obtained using Lagrangians and Hamiltonians but I did them on a paper