Wrote

You are totally right. rpm ► Hz

My Uconeer units converter does not have that idiosyncrasy.

Also, rpm may not be an SI unit, but it is a valid unit nonetheless. Just like troy ounces and avoirdupois ounces are both valid units (also not in SI), but they have different meanings.

And rpm IS a frequency. It's a rotational frequency (as Jopi stated) and is defined as 1/T, or the inverse of period. The period, in this case, is the time required to complete a specified number of revolutions:

1/60 min/rev = T

T = 60 rev/min

@overlord & @Razonar:

If you think I'm wrong, I challenge you to walk into your nearest university and try to convince three professors of physics, engineering, and/or math that 1 rad/s = 1 Hz. And please do video tape it...

At the very least, it'll be a teachable moment for you; at worst, they'll laugh you out of the building.

You could say that rad/s is a frequency (it is), but its meaning has limited use because it is dependent on/defined by an irrational number (π).

Wrote

@overlord & @Razonar:

If you think I'm wrong, I challenge you to walk into your nearest university and try to convince three professors of physics, engineering, and/or math that 1 rad/s = 1 Hz. And please do video tape it...

Hi. I'm quite sure this three guys think that rpm in SMath is well defined.







RPM_IN_PRACTICE.sm (562 КиБ) скачан 29 раз(а).

Alvaro.

Wrote

Hi. I'm quite sure this three guys think that rpm in SMath is well defined.

The following is the same calculation as the first example you provided, using the Windows Stable 0.99.7822 version of SMath (output units were not specified, except for the values on the line where it says "units specified" ).



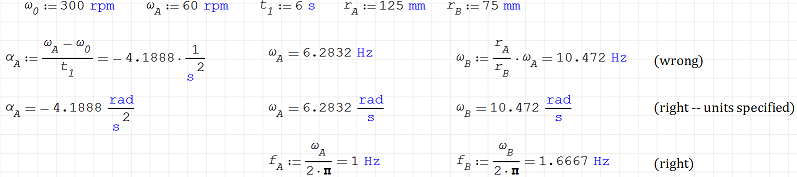
One could specify "rad/s" as the units, and no change would occur, which is fine for the first example that you provided (because SMath assumes that rad/s and 1/s are the exact same unit -- which they are, for angular velocities ONLY -- again, this is because radians are unitless), but it is absolutely incorrect as soon as FREQUENCY is required. SMath treats angular velocity or angular frequency (rad/s) and frequency (Hz or 1/s) as equal, which they aren't.

ω = 2 π f ~~~~ That's: (angular frequency) = 2 * (pi) * (frequency)

If you have a piston attached to disk B, then the frequency of the piston is EQUAL TO the frequency of the disk (NOT the angular frequency). Smath would calculate the frequency to be 10.472 Hz (wrong), when it would actually be 1.667 Hz (right).

This is because of how frequency is defined: it is the reciprocal of period, and period is the time it takes for a measurable event to occur. Frequency is therefore the times per second that the event occurs.

For angular frequency only, the period is the time it takes to rotate through an angle of ONE RADIAN (~57.3°). In other words, seconds per radian. Angular frequency is therefore the times per second that the object rotates by ~57.3°.

For most other applications, the period is the time it takes for a rotating OR oscillating object to pass its starting position. In other words, seconds per revolution or seconds per oscillation (cycle). Frequency is therefore the times per second that a roating or oscillating object passes its starting position.

I don't have time to go through the other examples. I've got homework to do, and I've gotta figure out workarounds to make SMath behave as expected with frequency, since it DOESN'T handle rpm <> Hz conversions properly, as evidenced by the very simple statement below:

Claiming SI units are wrong would be ridiculous.
This is how recent SI units are printed.
If they change it later in future, than I will defend what they write at that time.
If you want to achieve 0.0167 Hz in smath, use derived unit radpm.

Regards

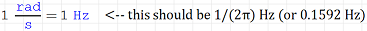
Wrote

Claiming SI units are wrong would be ridiculous.

Please, pray tell, where SPECIFICALLY does SI say that 1 Hz is approximately 57.3°/s (1 rad/s)? --- I am legitimately curious, because this defies everything I've learned in high school and in my engineering degree, and every source I've ever seen in my life... Please, correct the bias that I have clearly lived with for the past 20+ years!

I've looked - and I couldn't find any such reference. I've only found two things that together could (vaguely) define 1 Hz = 1 rad/s. Those two things were:
1) Hz is a "Periodic phenomena", and
2) Hz has units of "s^-1" (or "1/s" )

Considering said, NIST says to explicitly state radians when using rad/s, I highly doubt that anyone would come to the assumption that 1 Hz = 1 rad/s. They would (excepting yourself and Razonar) all come to the agreement that 1 Hz = 1 cycle/s = 1 rotation/sec = 1 oscillation/s = 1 revolution/s = etc.

Radians, on their own, are inherently not periodic (because it's defined using π). You cannot have an integer value of radians that returns you to 0°. The only way to get back to 0° is by multiplying radians by an even integer multiple of π.

Revolutions, on the other hand, ARE periodic.

EVERY source I can find that relates to SI units says something to the effect of "Hertz is the same as one cycle per second."

Know how many refer to Hertz as "one radian per second"?

Here's a hint: it starts with Z and ends with ero.

Wrote

If you want to achieve 0.0167 Hz in smath, use derived unit radpm.

Yeah, because everyone loves to use workarounds to do what is common practice in every other application and tool...

When you realize one revolution is not considered as 1, but as 2π in SI, then you will be convinced.
Otherwise, I can do nothing. There lays all standardization documents. Read them, carefully, and be ready to your world destructed in shambles.

No need to argue, let's agree to disagree. But SMath's units shall respect to SI units, beware of that.

Wrote

When you realize one revolution is not considered as 1, but as 2π in SI, then you will be convinced.

1 revolution is NOT 2 pi.

1 revolution is 2 pi radians.

As you know, it's based on the circle: 1 radian = angle at which the arc length along a circle is equal to its radius (θ = S/R = 1 rad), which is basically a fancy way of saying that C = 2πR = πD.

I suspected you'd give a "go read the standard" response. But I'm giving you the benefit of the doubt, here... point me in the right direction. Give me a reference (non-paywalled resource, or a DOI or journal that is likely to be accessible through my university) and a page number(s) or section(s) upon which you're basing your claim.

The copies of the SI standard that I found do not explicitly define frequency in a manner congruent with your 1 rad/s = 1 Hz claim, so please... use this as a teaching moment and give me the source by which you're defining frequency.

Wrote

Wrote

Hi. I'm quite sure this three guys think that rpm in SMath is well defined.

The following is the same calculation as the first example you provided, using the Windows Stable 0.99.7822 version of SMath (output units were not specified, except for the values on the line where it says "units specified" ).

Nope. Your error is here:

Wrote

1 [rad] = (Circumferential path segment that is the same length as the radius)/(Radius) = [m]/[m] = [unitless]

QED.

I don't specify units, I (and those three guys, if you don't know them, it could be a good read for introduce some basics) specify dimensions, not units. Radians are not unitless, they are an unit, are dimensionless, which isn't the same. For instance, masons, architects and civil engineers often measure the slopes of their angles in buildings in cm / m, quantities that are dimensionless but certainly have units.

Following your line of reasoning, you should tell Norton to correct his book, as his torque values (lbf-in) are badly wrong because he forgot to include radians. Or you don't measeure torques in energy units? Because I do. And Norton too.



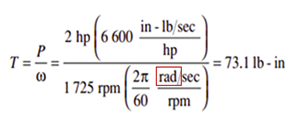
Alvaro.

Radians are taken as 1, historically.
Hence it is 1 SMath just eliminate it, practically.

I didn't wrote the SI documents, I just obey them.
And if you will doubt on worldwide accepted scientific standards, fine for me.
I doubt from everything every time. But I know I am not that clever than scientists.
When I read scientific documents I clear my doubts if they convince me.
Here I gave two SI document, BIPM and NIST. They all say 1 rpm = 0.1407 Hz.
I don't know your documents resources, you haven't given any.

If you think you are right, apply to CGPM with your arguments.

Wrote

Nope. Your error is here:

I concede that I used the wrong word (unitless), but the difference is semantic only. The intended meaning is not changed by using "dimensionless" instead.


As overlord included in a recent response, SMath interprets rads per minute in the same way that most people interpret revolutions per minute, and vice-versa. Which is wholly confusing:

60 rpm = 2π Hz
60 radpm = 1 Hz

versus:

60 rad/min = 60/(2π) revolutions/min = 1/(2π) cycle/s = 1/(2π) Hz


And it makes sense that the "frequency" in torque is angular frequency, because torque is the rotational equivalent to a moment (force x distance) and work (force x distance). Radians provide a 1:1 relationship between rotational work and linear work.

But Hz is a unit of (inverse) time. As far as I can tell, the SI standard ALLOWS for rad = (1) when used with Hz, but it doesn't define it as such. (In fact, it seems horribly obstinate about such a definition.)

I would argue that the "long-established practice ... of rad = 1" is equally as common as the understanding of Hz = 1 cycle/s (where, by SI definition, "cycle" is also dimensionless and thus cycle = 1).

It's clear from what I've read that both "1 rad/s = 1 Hz" and "1 cycle/s = 1 Hz" are acceptable by SI standards, and both have their uses, but when you says "This value is ___ Hz" to 99% of the scientific community, they'll assume you mean "This value is ___ cycles per second" (unless the context provides clues otherwise, such as when using ω or when speaking specifically about angular frequency, such as with torque).

So, I would argue that since both are "accepted" and that 1 Hz = 1 cycle/s is the definition MUCH more widely assumed and understood when speaking about frequency, that SMath should treat Hz as cycles per second, along with rpm as cycles per minute, and use rad/s for radians per second and radpm as radians per minute. At the very least, such a change would be more user-friendly and align with the behaviour that the astounding majority of users would expect.

Wrote

I didn't wrote the SI documents, I just obey them.

See, that's the thing... this is seeming to be a lot more about "interpreting scripture" than it is about applying a concrete standard.

The section of the SI standard that you shared is precisely the section that I have been reading carefully and, by my best judgment, it merely states that both sides of this argument are right.

"make use of" is not the same as "exclusively use". ω is used commonly across math and science (and is most commonly associated with units of rad/s), while f is used just as widely (and is most commonly associated with units of Hz). It's so rare to conflate the two that, before now, I've never seen ω defined in units of Hz (though I have seen ω used, rarely, with rpm).

This paper sums up my meaning: Dimensionless units in the SI

Wrote

Wrote

I didn't wrote the SI documents, I just obey them.

See, that's the thing... this is seeming to be a lot more about "interpreting scripture" than it is about applying a concrete standard.

What I have written before that statement is;

Wrote

This is how recent SI units are printed.
If they change it later in future, than I will defend what they write at that time.

I didn't know "scriptures" can be changed.
What kind of religious belief you are in?
I see your ad hominem and withdraw my hand.

Your logic about standards is crippled.
This is science, of course I shall obey its standards and rules.
Until a better rule in it is found and replaced the old one.
Maybe I find the new rule maybe another. (I know I won't)
But it has to be written in related standard.

And the page you have shared is just an article, a paper.
Anyone can write a paper about anything, even with bizarre arguments.
I am not saying all articles has nonsense information. (yours has)
But they should not to be taken as standard's replacements.

Wrote

...
This paper sums up my meaning: Dimensionless units in the SI

From your paper, here is the problem:



As I say before, all books are wrong with that convention. This is: Torque must to have radians. Can you imagine calculating a Lagrangian, or worse, an action integral, with those units?

Best regards.
Alvaro.

Wrote

I see your ad hominem and withdraw my hand.

It's a metaphor, not a personal attack...

Wrote

Your logic about standards is crippled.

"Immature" may be more accurate here, but the difference is semantically insignificant, given our mutual lack of acquaintance with one another.

Wrote

This is science...

This is technical writing (an important compliment to science). Science is required to develop the content, and may be involved in some of the decisions, certainly. But on the whole, standards are about communication - and with communication, clarity is king.

Wrote

And the page you have shared is just an article, a paper...they should not to be taken as standard's replacements.

I wasn't implying that the paper overturns the standard (that would be silly). The paper was simply referenced because it highlights the type of ambiguities that have been the source of my frustration and the core of this debate.

Wrote

As I say before, all books are wrong with that convention. This is: Torque must to have radians.

I fail to see how that is relevant.

I'm not suggesting that torque shouldn't use radians.

I'm merely suggesting that the use of radians in frequency should be *explicit* in SMath (i.e. that frequency in Hz should be assumed as cycles/s, not rad/s), to conform more to how most calculations are commonly performed on paper. OR that SMath should come up with a way to allow the user to select the behavior in this case. (For example, perhaps a "rigid standards" mode vs "common usage" mode.)

As an example, motor power is not calculated from RPM without first converting to rad/s, and most industrial motors rotate at a fixed ratio w.r.t. the electrical supply frequency (i.e. ω = A * 2π * f), where A is the ratio, and f is the supply frequency. Having to use workarounds and double-check that the output units are functioning as expected every time can become rather cumbersome. In my case, it's sufficiently bothersome that using SMath (which is typically my go-to for this type of assignment) could unnecessarily complicate my combinations this time around.

Wrote

Wrote

This is science...

This is technical writing (an important compliment to science). Science is required to develop the content, and may be involved in some of the decisions, certainly. But on the whole, standards are about communication - and with communication, clarity is king.

Nope, you are wrong.

This is the definition I gathered from Oxford University Press:
Science encompasses the systematic study of the structure and behaviour of the physical and natural world through observation and experiment.
Technology is the application of scientific knowledge for practical purposes.

Defining units and standardizing them is science.
Science establish a base for further use with defining units.
They are even called scientific units, not technical units.

Using scientific knowledge for calculations is technology.
And you calculate technology with technical writings.

Engineers use Engineering Units.
SI does not explicit my bench saw motor radiates sin/cos Hz.
The demo rkfixed RPM could be animated.
No reconciliation so far ... Jean.

Circle_rkfixed RPM.sm (12 КиБ) скачан 28 раз(а).

Wrote

Engineers use Engineering Units.
SI does not explicit my bench saw motor radiates sin/cos Hz.

There is no term as Engineering Units in SI. That is an imperial units or derivations term.
Which is used only by 3 countries in whole world; USA, England and Myanmar.
I guess Canadians are having problems too due to their late acknowledge of metric system.

Wrote

Nope, you are wrong.

This is the definition I gathered from Oxford University Press:
Science encompasses the systematic study of the structure and behaviour of the physical and natural world through observation and experiment.
Technology is the application of scientific knowledge for practical purposes.

Defining units and standardizing them is science.
Science establish a base for further use with defining units.
They are even called scientific units, not technical units.

Using scientific knowledge for calculations is technology.
And you calculate technology with technical writings.

Oh my word... STANDARDS are not science.

Standards are technical writing. Some science may be involved in structuring them (i.e. how they are written, the methods they used to communicate, etc.), but the WHOLE PURPOSE of technical writing is to communicate scientific knowledge (which is developed through science). But standards, themselves, are NOT science. They are a communication tool, nothing more. They are what is compiled after the science is done (and re-done, and re-done again) to provide a common foundation.

Just like there's clearly some misunderstandings in our communications here, even though we are using a common standard (English) to communicate, there are bound to be misunderstandings with technical communications, such as standards. But with dozens (or hundreds? thousands?) of people developing those standards, one would expect that they would be less ambiguous.