1 страниц (14 вхождений)
problem with conversion rpm - Сообщения
Anyone try unit rpm (rotation per minute or revolution per minute)
I typed 1500 rpm (unit rpm) then typed =
and I found incorrect result in rad/s.
The correct result if I multiply the result by 2.pi
I use beta version in Windows.
Regards
Waluyo
I typed 1500 rpm (unit rpm) then typed =
and I found incorrect result in rad/s.
The correct result if I multiply the result by 2.pi
I use beta version in Windows.
Regards
Waluyo
Yes, I tried... but I found that the correct unit is "radpm" that is defined in Smath as "pi/30s".
But "radpm" is not common, and I never use "radpm". I don't think this is listed as SI.
I have doubled check in the Guide for the Use of the International System of Units (SI), and I could not find "radpm"
I think users will get incorrect result since they think "rpm" in SMath is the common standard that people usually use, but in fact the conversion is different?
I have doubled check in the Guide for the Use of the International System of Units (SI), and I could not find "radpm"
I think users will get incorrect result since they think "rpm" in SMath is the common standard that people usually use, but in fact the conversion is different?
I also confirm that the pre-defined unit rpm (revolutions per minute) is defined incorrectly in Smath.
It should be 1 rpm = 2*pi / 60 sec = pi / 30 sec .
The unit radpm (radians per minute) is also defined incorrectly.
It should be 1 radpm = 1 / 60 sec.
It appears that the definitions of these two units were accidentally switched. This error should be fixed soon.
I am using Smath Stable in Windows.
It should be 1 rpm = 2*pi / 60 sec = pi / 30 sec .
The unit radpm (radians per minute) is also defined incorrectly.
It should be 1 radpm = 1 / 60 sec.
It appears that the definitions of these two units were accidentally switched. This error should be fixed soon.
I am using Smath Stable in Windows.
Will Massie
Mechanical Engineer
Oregon, USA
In my opinion the units for the rotational speed and angular speed are correct.
The unit of n is defined as "revolutions per time": 1rpm = 1/min = 1/60s
In the other hand we have the angular speed omega = 2 * PI * n
The unit of omega is defined as "angle per time": 1rad/s = 60rad/min = 360/2PI°/s
But we can write 1rpm = 1/min and 1rad/min = 1/min.
Here we have to be careful, it is important to keep in mind the physical context.
As example see mechanical work and torque: 1Joule = 1kg*m²/s² and 1Nm = 1kg*m²/s²
Best Regards,
Peter
The unit of n is defined as "revolutions per time": 1rpm = 1/min = 1/60s
In the other hand we have the angular speed omega = 2 * PI * n
The unit of omega is defined as "angle per time": 1rad/s = 60rad/min = 360/2PI°/s
But we can write 1rpm = 1/min and 1rad/min = 1/min.
Here we have to be careful, it is important to keep in mind the physical context.
As example see mechanical work and torque: 1Joule = 1kg*m²/s² and 1Nm = 1kg*m²/s²
Best Regards,
Peter
Peter,
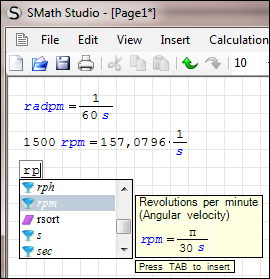
I see what you mean. In regards to "rpm" (revolutions per minute), I think that you are correct. While in practice "rpm" can be used to measure "angular velocity" it is technically better referred to as a measure of "angular frequency" (cycles per unit of time). Thus, 1 rpm = 1 / 60 sec = 0.01667 Hz would be correct, as shown in the Smath screen shot below, where "rpm" is, in my opinion, correctly referred to as a unit of "frequency":

Angular frequency is, of course, directly related to angular velocity. In Smath, it would be best to convert angular frequency to angular velocity the old fashioned way:

However, regarding the built-in Smath unit "radpm", I still think this unit is defined incorrectly. As shown in the Smath screenshot below:

In my opinion, I think the unit "radpm" should be referred to as a measure of "angular velocity" not "frequency" in order to distinguish it from "rpm". Also, it should be defined as 1 radpm = 1 / 60 sec. If we use the same formula above but use "radpm" instead of "rad/min", Smath gives the following erroneous result:

However, redefining the unit "radpm" as 1 radpm = 1 / 60 sec allows Smath to calculate the correct result:

This could, of course, allow the user to reach incorrect results if they tried to convert "rpm" directly to "radpm" or "rad/min" using Smath's built-in unit translator. But, if we distinguish between these two units by defining "rpm" as a measure of "frequency" and "radpm" as a measure of "angular velocity", this would, as you pointed out already, be analogous to the situation between mechanical work and torque: 1Joule = 1kg*m²/s² and 1Nm = 1kg*m²/s². The user simply needs to be mindful of the distinction to avoid making an error.
I see what you mean. In regards to "rpm" (revolutions per minute), I think that you are correct. While in practice "rpm" can be used to measure "angular velocity" it is technically better referred to as a measure of "angular frequency" (cycles per unit of time). Thus, 1 rpm = 1 / 60 sec = 0.01667 Hz would be correct, as shown in the Smath screen shot below, where "rpm" is, in my opinion, correctly referred to as a unit of "frequency":

Angular frequency is, of course, directly related to angular velocity. In Smath, it would be best to convert angular frequency to angular velocity the old fashioned way:

However, regarding the built-in Smath unit "radpm", I still think this unit is defined incorrectly. As shown in the Smath screenshot below:

In my opinion, I think the unit "radpm" should be referred to as a measure of "angular velocity" not "frequency" in order to distinguish it from "rpm". Also, it should be defined as 1 radpm = 1 / 60 sec. If we use the same formula above but use "radpm" instead of "rad/min", Smath gives the following erroneous result:

However, redefining the unit "radpm" as 1 radpm = 1 / 60 sec allows Smath to calculate the correct result:

This could, of course, allow the user to reach incorrect results if they tried to convert "rpm" directly to "radpm" or "rad/min" using Smath's built-in unit translator. But, if we distinguish between these two units by defining "rpm" as a measure of "frequency" and "radpm" as a measure of "angular velocity", this would, as you pointed out already, be analogous to the situation between mechanical work and torque: 1Joule = 1kg*m²/s² and 1Nm = 1kg*m²/s². The user simply needs to be mindful of the distinction to avoid making an error.
Will Massie
Mechanical Engineer
Oregon, USA
Hello SMath
I just try the latest version 0.9. I tried to convert rotation 1500 rpm to rad/s, the result is still the same =25 rad/s (which is incorrect).
The rotation 1500 RPM is always converted to angular velocity omega=(1500*2*pi/60) rad/s = 157.08 rad/s.
Perhaps, as benchmarking, try mathcad or unit conversion rpm to rad/s.
I agree with Will Massie in the previous post.
Regards
waluyo
I just try the latest version 0.9. I tried to convert rotation 1500 rpm to rad/s, the result is still the same =25 rad/s (which is incorrect).
The rotation 1500 RPM is always converted to angular velocity omega=(1500*2*pi/60) rad/s = 157.08 rad/s.
Perhaps, as benchmarking, try mathcad or unit conversion rpm to rad/s.
I agree with Will Massie in the previous post.
Regards
waluyo
This is the conversion provided by wolframalpha
http://www.wolframalpha.com/input/?i=1500+rpm
regards
waluyo
http://www.wolframalpha.com/input/?i=1500+rpm
regards
waluyo
Fixed.
'rpm unit moved from Frequency to Angular Velocity.
'rpm = π/(30*'s)
'rph added to Angular Velocity as π/(1800*'s).
'radpm = 1/(60*'s)
Best regards, Andrey Ivashov.
'rpm unit moved from Frequency to Angular Velocity.
'rpm = π/(30*'s)
'rph added to Angular Velocity as π/(1800*'s).
'radpm = 1/(60*'s)
Best regards, Andrey Ivashov.
Great. Thanks Andrey for fixing.
Steve
Steve
It seems that this issue from 10 years ago has resurfaced (I'm using version 0.99 Build 7822 on 64-bit Windows 10). I'm responding to this long dead thread, since this is clearly the same problem as before, and a Google search didn't find any other similar problems).
SMath (erroneously) produces:
1 rpm = 0.1047 Hz (= 2π/60 Hz)
1 radpm = 0.0167 Hz (= 1/60 Hz)
2π Hz = 60 rpm (= 1 rev/s)
2π rad/s = 6.2832 Hz (= 2π Hz)
Doing a manual unit conversion (paper method) reveals that the above values are wrong:
1 rpm = 1 rev/min * (1 min)/(60 s) = 1/60 * rev/s = 0.0167 Hz ====> (NOT: 0.1047 Hz)
1 radpm = 1 rad/min * (1 min)/(60 s) * (1 rev)/(2π rad) = 0.00265 Hz = 1/(60*2π) Hz = 1/(120π) Hz ====> (NOT: 0.0167 Hz)
2π Hz = 2π cycle/s = 2π rev/s * (60 s)/(1 min) = 2π*60 rev/min = 120π rpm = 376.99 rpm ====> (NOT: 60 rpm)
2π rad/s = 2π rad/s * (1 rev)/(2π rad) = 1 rev/s = 1 Hz ====> (NOT: 2π Hz)
Oddly, SMath does have the units right for both rev|rad and min|s:
1 rev = 6.2832 rad = 2π rad
1 rad = 0.1592 rev = 1/(2π) rev
1 min = 60 s
1 s = 0.0167 min
But as soon as they're combined with time, SMath manages to mess up the calculation:
1 Hz = 1 rad/s ====> (should be) ====> 2π rad/s
1 rev/min = 1 rpm = 0.1047 Hz ====> (should be) ====> 1 rev/min = 0.0167 Hz
1 rad/min = 1 radpm = 0.0167 Hz = 1/(60 s) = 1/60 s^-1 ====> (should be) ====> (1/60 rad/s OR (1 rad)/(60 s) --- maweilian's proposal about radpm incorrect... what he said should be applied to rpm, NOT radpm).
One rev/cycle/rotation is basically the "real" unitless value. Everything else is defined therefrom: 1 rotation = 1 cycle = 1 revolution = 360° = 2π rad = 4 quarters, etc.
Since Hz is defined as "one cycle per second" (1/s), it is a unit of frequency. rpm is a unit of angular *frequency*, while radpm is a unit of angular *velocity*. Therefore, rpm should be defined in terms of 1/s, or "cycles per unit time" while radpm should be defined in terms of rad/s, or "radians per unit time". In other words, radians [rad] are defined with respect to cycles [] by:
1 [] = 2π [rad] ===> [rad] = 1/(2π) []
Making rpm and radpm defined with respect to frequency ([Hz] = []/[s]):
rpm = [rev]/[min] = []/[min] * (1 [min])/(60 [s]) = 1/60 []/[s] = 1/60 [Hz]
radpm = [rad]/[min] * (1 [])/(2π [rad]) * (1 [min])/(60 [s]) = 1/(2π*60) []/[s] = 1/(120π) [Hz]
SMath (erroneously) produces:
1 rpm = 0.1047 Hz (= 2π/60 Hz)
1 radpm = 0.0167 Hz (= 1/60 Hz)
2π Hz = 60 rpm (= 1 rev/s)
2π rad/s = 6.2832 Hz (= 2π Hz)
Doing a manual unit conversion (paper method) reveals that the above values are wrong:
1 rpm = 1 rev/min * (1 min)/(60 s) = 1/60 * rev/s = 0.0167 Hz ====> (NOT: 0.1047 Hz)
1 radpm = 1 rad/min * (1 min)/(60 s) * (1 rev)/(2π rad) = 0.00265 Hz = 1/(60*2π) Hz = 1/(120π) Hz ====> (NOT: 0.0167 Hz)
2π Hz = 2π cycle/s = 2π rev/s * (60 s)/(1 min) = 2π*60 rev/min = 120π rpm = 376.99 rpm ====> (NOT: 60 rpm)
2π rad/s = 2π rad/s * (1 rev)/(2π rad) = 1 rev/s = 1 Hz ====> (NOT: 2π Hz)
Oddly, SMath does have the units right for both rev|rad and min|s:
1 rev = 6.2832 rad = 2π rad
1 rad = 0.1592 rev = 1/(2π) rev
1 min = 60 s
1 s = 0.0167 min
But as soon as they're combined with time, SMath manages to mess up the calculation:
1 Hz = 1 rad/s ====> (should be) ====> 2π rad/s
1 rev/min = 1 rpm = 0.1047 Hz ====> (should be) ====> 1 rev/min = 0.0167 Hz
1 rad/min = 1 radpm = 0.0167 Hz = 1/(60 s) = 1/60 s^-1 ====> (should be) ====> (1/60 rad/s OR (1 rad)/(60 s) --- maweilian's proposal about radpm incorrect... what he said should be applied to rpm, NOT radpm).
One rev/cycle/rotation is basically the "real" unitless value. Everything else is defined therefrom: 1 rotation = 1 cycle = 1 revolution = 360° = 2π rad = 4 quarters, etc.
Since Hz is defined as "one cycle per second" (1/s), it is a unit of frequency. rpm is a unit of angular *frequency*, while radpm is a unit of angular *velocity*. Therefore, rpm should be defined in terms of 1/s, or "cycles per unit time" while radpm should be defined in terms of rad/s, or "radians per unit time". In other words, radians [rad] are defined with respect to cycles [] by:
1 [] = 2π [rad] ===> [rad] = 1/(2π) []
Making rpm and radpm defined with respect to frequency ([Hz] = []/[s]):
rpm = [rev]/[min] = []/[min] * (1 [min])/(60 [s]) = 1/60 []/[s] = 1/60 [Hz]
radpm = [rad]/[min] * (1 [])/(2π [rad]) * (1 [min])/(60 [s]) = 1/(2π*60) []/[s] = 1/(120π) [Hz]
WroteSMath (erroneously) produces:
1 rpm = 0.1047 Hz (= 2π/60 Hz)
1 radpm = 0.0167 Hz (= 1/60 Hz)
2π Hz = 60 rpm (= 1 rev/s)
2π rad/s = 6.2832 Hz (= 2π Hz)
This has been discussed recently.
Nothing is wrong with rpm in SMath.
Please check responds of Razonar's and mine.
Regards
https://en.smath.com/forum/yaf_postsm74154_rpm-to-rad-s.aspx#post74154
WroteThis has been discussed recently.
Nothing is wrong with rpm in SMath.
Please check responds of Razonar's and mine.
You are mistaken. RPM in SMath is broken (see my responses on the thread you referenced, as well as my remarks below).
The misunderstanding likely comes from interpreting rpm strictly as an angular velocity (which it technically is), when it is more accurate to call it a rotational frequency. If you drive a piston from a journal bearing on a crankshaft, the frequency of that piston, in Hz (from top-dead-centre to the subsequent top-dead-centre) is equal to one-sixtieth of the cranshaft rpm.
The frequency of the shaft is equal to the frequency at which the shaft returns to the same position (and therefore results in the same piston position), or how frequently it passes n*2π radians from its starting position, where n is the number of turns (revolutions) since measurement started.
At 3000 rpm, that's a rotational frequency of 50 Hz, and a piston frequency of 50 Hz (NOT 314.1593 Hz).
The crankshaft would be turning at an angular velocity of: 50 Hz * (2π rad/s)/(1 Hz) = 100π rad/s = 314.1593 rad/s (again, NOT 314.1593 Hz).
WroteYou are mistaken.
Nope, I am not.
If am wrong than SI documents are wrong. Which they are not.
Claiming SI units are wrong would be ridiculous.
This is how recent SI units are printed.
If they change it later in future, than I will defend what they write at that time.
If you want to achieve 0.0167 Hz in smath, use derived unit radpm.
Regards

1 страниц (14 вхождений)
- Новые сообщения
- Нет новых сообщений
